 |
A P. 5135. feladat (2019. május) |
P. 5135. Vízszintes talajon álló autóba beszálló, \(\displaystyle G=840\) N súlyú vezető tömegközéppontja az ábrán látható \(\displaystyle A\) pontba kerül. (A méreteket az ábra jobb oldali része felülnézetből, méretarányosan mutatja. Az \(\displaystyle A\) pont a kerekek által meghatározott téglalapban a bal első és a jobb hátsó kereket összekötő átló első harmadolópontja.) Mennyivel nő meg az egyes kerekekre ható nyomóerő a vezető nélküli esethez képest? A kerekek rugói egyformák, és követik a Hooke-törvényt.
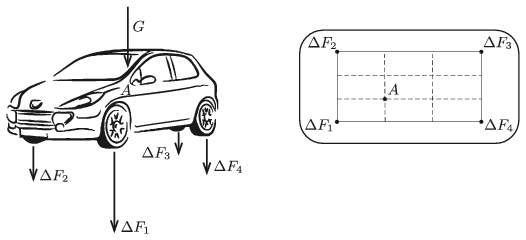
Közli: Németh László, Fonyód
(5 pont)
A beküldési határidő 2019. június 11-én LEJÁRT.
Megoldás. A gépkocsira ható erők eredője és a forgatónyomatékuk eredője a vezető beszállása előtt is és utána is nulla. Emiatt az erők megváltozásai önmagukban is erőegyensúlyt eredményeznek:
| \(\displaystyle (1)\) | \(\displaystyle \Delta F_1+\Delta F_2+\Delta F_3+\Delta F_4=G,\) |
az \(\displaystyle A\) ponton átmenő hosszanti, illetve keresztirányú tengelyekre vonatkozó forgatónyomatékok egyensúlyából:
| \(\displaystyle (2)\) | \(\displaystyle \Delta F_1+\Delta F_2=2(\Delta F_3+\Delta F_4),\) |
valamint
| \(\displaystyle (3)\) | \(\displaystyle \Delta F_1+\Delta F_4=2(\Delta F_2+\Delta F_3).\) |
(Ha más tengelyekre írjuk fel a forgatónyomatékok egyensúlyát, az már nem ad új információt, hanem (2) és (3) ismeretében azonosságokat eredményez.)
A negyedik egyenletet a gépkocsi alvázának merevsége adja. A többleterőkkel arányos kerékelmozdulások egy-egy átló menti számtani közepe a gépkocsi középpontjának elmozdulását adja, ami mindkét átlóra ugyanakkora kell, hogy legyen:
| \(\displaystyle (4)\) | \(\displaystyle \frac{\Delta F_1+\Delta F_3}{2}=\frac{\Delta F_2+\Delta F_4}{2}.\) |
Az (1)-(4) egyenletek meghatározzák az egyes kerekekre ható erő megváltozását:
\(\displaystyle \Delta F_1=\frac{5}{12}\,G=350~\rm N,\)
\(\displaystyle \Delta F_2=\Delta F_4=\frac{3}{12}\,G=210~\rm N,\)
\(\displaystyle \Delta F_3=\frac{1}{12}\,G=70~\rm N.\)
Statisztika:
17 dolgozat érkezett. 5 pontot kapott: Bokor Endre, Hervay Bence, Marozsák Tádé, Olosz Adél, Sas 202 Mór, Tiefenbeck Flórián, Vaszary Tamás. 4 pontot kapott: Bukor Benedek, Nagyváradi Dániel, Varga Vázsony. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2019. májusi fizika feladatai
