A P. 5147. feladat (2019. szeptember)

P. 5147. A Pécs–Pogány Repülőtéren repülőnapot rendeznek. Reklám céljából egy \(\displaystyle V=10~\rm m^3\) térfogatú, héliummal töltött ballont engednek a magasba súlytalannak tekinthető kötélen. A ballon anyagának térfogata elhanyagolható, töltetlen tömege \(\displaystyle m=2~\rm kg\). A hőmérséklet a ballon belsejében, illetve annak külső környezetében \(\displaystyle T=300\) K, a külső légnyomás \(\displaystyle p_0=10^5\) Pa. A ballon anyagának rugalmasságából származó nyomástól eltekintünk.

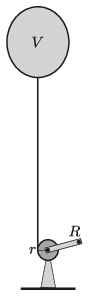
A rendezvény végén a ballont csörlővel lassan levonják. A csörlő hengerének sugara \(\displaystyle r=10\) cm, a hajtókar sugara \(\displaystyle R=30\) cm. A közegellenállás elhanyagolható.

\(\displaystyle a)\) Mekkora erőt kell a hajtókarra kifejteni a ballon egyenletes lehúzása esetén?

\(\displaystyle b)\) Mekkora teljesítmény szükséges a levonáshoz, ha a ballon \(\displaystyle v=1\) m/s sebességgel süllyed?

Párkányi László fizikaverseny, Pécs

(4 pont)

A beküldési határidő 2019. október 10-én LEJÁRT.

Megoldás. A hélium moláris tömege \(\displaystyle M_\text{He}=4\) g/mol, a levegő átlagos moláris tömege \(\displaystyle M_\text{lev.}=29\) g/mol. A gáztörvényből kiszámíthatjuk a hélium és a kiszorított levegő tömegét:

\(\displaystyle m_\text{He}=\frac{p_0 V}{RT}M_\text{He}=1{,}6~\rm kg,\)

\(\displaystyle m_\text{lev.}=\frac{p_0 V}{RT}M_\text{lev.}=11{,}6~\rm kg.\)

Az egyenletesen mozgó ballonra ható erők eredője nulla:

\(\displaystyle F+ m_\text{He}g+mg-m_\text{lev.}g=0,\)

ahonnan a kötelet feszítő erő:

\(\displaystyle F=\left(m_\text{lev.}-m_\text{He}-m\right)g=8{,}0~{\rm kg}\cdot 9{,}81~\frac{\rm m}{\rm s^2}=78{,}5~\rm N.\)

\(\displaystyle a)\) A hajtókarra (a csörlőre ható forgatónyomatékok egyensúlya miatt) \(\displaystyle F'=\frac{r}{R}F=\frac{1}{3}F=26{,}2~\rm N\) erőt kell kifejteni.

\(\displaystyle b)\) A ballon lehúzásához szükséges teljesítmény: \(\displaystyle P=Fv=78{,}5~\rm W.\)

Statisztika:

71 dolgozat érkezett.
4 pontot kapott:	Amrein Roland, Bánáti Tamás, Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Dékány Csaba, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Gurzó József, Györgyfalvai Fanni, Hartmann Alice, Jánosik Áron, Kardkovács Levente, Kis-Bogdán Kolos, Laposa Hédi, Lengyel Barnabás, Ludányi Levente, Mihalik Bálint, Németh Kristóf, Perényi Barnabás, Schneider Anna, Selmi Bálint, Somlán Gellért, Szabó 314 László, Szikora 417 Viktor, Tanács Kristóf, Tanner Norman, Toronyi András, Török 111 László, Vass Bence.
3 pontot kapott:	24 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2019. szeptemberi fizika feladatai