A P. 5199. feladat (2020. február)

P. 5199. Az ábrán látható \(\displaystyle \ell\) hosszú, körív alakú, vékony (de kellően merev) fémhuzal mindkét végpontját \(\displaystyle \ell\) hosszúságú, igen könnyű fonállal a körív \(\displaystyle O\) középpontjához erősítjük. Az így elkészített inga az ábra függőleges síkjában \(\displaystyle T_1\) periódusidejű, kis kitérésű lengéseket végezhet az \(\displaystyle O\) pont körül. Ha a fémhuzalt kiegyenesítjük, az így átalakított test az ábra síkjában \(\displaystyle T_2\) periódusidejű, kis kitérésű lengéseket végezhet. Mekkora a \(\displaystyle T_2/T_1\) arány?

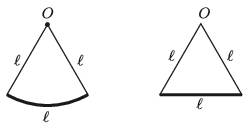
Közli: Simon Péter, Pécs

(5 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

Megoldás. Mindkét esetben alkalmazhatjuk a fizikai inga lengésidejének

\(\displaystyle T=2\pi\sqrt{\frac{\Theta}{mgs}}\)

képletét, ahol \(\displaystyle s\) a tömegközéppont és az \(\displaystyle O\) pont távolsága, \(\displaystyle \Theta\) pedig az \(\displaystyle O\) pontra vonatkozó tehetetlenségi nyomaték.

Az első esetben a körív nyílásszöge \(\displaystyle 2\alpha=1\) radián (kb. \(\displaystyle 57{,}3^\circ\)), a tehetetlenségi nyomaték pedig \(\displaystyle m\ell^2\), hiszen a körív minden pontja \(\displaystyle \ell\) távolságra van a forgástengelytől. A súlypont és az \(\displaystyle O\) pont távolsága az

\(\displaystyle s=\frac{2(R^3-r^3)}{3(R^2-r^2)}\,\frac{\sin\alpha}{\alpha}\)

összefüggésből (lásd pl. Négyjegyű függvénytáblázatok 197. oldalát) határozható meg, ha az \(\displaystyle R\approx r\approx \ell\) határesetet vizsgáljuk:

\(\displaystyle s=\frac{\sin\alpha}{\alpha}\ell\approx 0{,}96\,\ell.\)

Ezek szerint

\(\displaystyle T_1=2\pi\sqrt{1{,}04\,\frac{\ell}{g}}. \)

A második esetben (a kiegyenesített fémhuzalnál) a tömegközéppont a huzal középpontjánál lesz, tehát

\(\displaystyle s=\ell\,\cos30^\circ\approx 0{,}866\,\ell,\)

a tehetetlenségi nyomaték pedig a Steiner-tétel alapján

\(\displaystyle \Theta=\frac{1}{12}m\ell^2+m\ell^2\,\cos^2 30^\circ=m\ell^2\left(\frac{1}{12}+\frac{3}{4}\right)=\frac{5}{6}m\ell^2.\)

A lengésidő ebben az esetben:

\(\displaystyle T_2=2\pi\sqrt{0{,}96\frac{\ell}{g}}.\)

A keresett arány:

\(\displaystyle \frac{T_2}{T_1}=\sqrt{ \frac{0{,}96}{1{,}04}} \approx 0{,}96.\)

Statisztika:

34 dolgozat érkezett.
5 pontot kapott:	Balázs 825 Ádám , Bokor Endre, Fekete Levente, Fonyi Máté Sándor, Györgyfalvai Fanni, Jánosik Áron, Kertész Balázs, Ludányi Levente, Sas 202 Mór, Téglás Panna, Toronyi András, Török 111 László, Vass Bence, Viczián Anna.
4 pontot kapott:	Fekete András Albert, Fülöp Sámuel Sihombing, Hamar Dávid, Horváth 999 Anikó, Nagyváradi Dániel, Schäffer Bálint, Sepsi Csombor Márton, Somlán Gellért, Szabó 314 László, Tóth Ábel.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2020. februári fizika feladatai