A P. 5204. feladat (2020. február)

P. 5204. Határozzuk meg az ábrán vázolt katódsugaras oszcilloszkópcső érzékenységét mm/volt egységben!

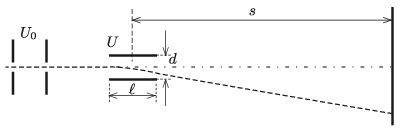
Adatok: az eltérítőlemezek hossza \(\displaystyle \ell=2\) cm, a lemezek távolsága \(\displaystyle d= 0{,}5\) cm, az ernyő távolsága a lemezek közepétől \(\displaystyle s=20\) cm, a gyorsítófeszültség \(\displaystyle U_0=1000\) V, és az eltérítőfeszültség legnagyobb értéke \(\displaystyle U_\text{max}=100\) V.

Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

Megoldás. Az \(\displaystyle e\) töltésű, \(\displaystyle m\) tömegű elektronok \(\displaystyle \frac{1}{2}mv_0^2=eU_0\) mozgási energiával, tehát

\(\displaystyle v_0=\sqrt{\frac{2eU_0}{m}}\)

sebességgel érkeznek az eltérítólemezek közé, és ezt (az ábrán vízszintes irányú) sebességkomponensüket a továbbiakban is megtartják. A lemezek közötti útszakaszt

\(\displaystyle t_1=\frac{\ell}{v_0},\)

a további útszakaszt pedig

\(\displaystyle t_2=\frac{s- (\ell/2)}{v_0}\)

idő alatt teszik meg az elektronok.

Az \(\displaystyle U\) feszültségű eltérítőlemezek között az \(\displaystyle E=U/d\) térerősség hatására az elektronok (az ábrának megfelelően) függőlegesen lefelé

\(\displaystyle a=\frac{eE}{m}=\frac{eU}{md}\)

gyorsulással mozognak. A lemezek közt áthaladva a függőleges elmozdulásuk

\(\displaystyle y_1=\frac{a}{2}t_1^2,\)

a kialakuló függőleges sebességük nagysága pedig

\(\displaystyle v_\text{le}=at_1.\)

Az ernyőig haladva a további függőleges irányú elmozdulásuk: \(\displaystyle y_2=v_\text{le}t_2\).

A fenti összefüggésekből azt kapjuk, hogy az ernyőnek csapódó elektron összes függőleges elmozdulása

\(\displaystyle y=y_1+y_2=\frac{s\ell}{2dU_0}\, U=0{,}4~\frac{\rm mm}{\rm V}\, U.\)

Ebben a képletben szereplő 0,4 mm/V arányossági tényező az oszcilloszkóp érzékenysége. Látható, hogy az érzékenység független az eltérítő feszültségtől. (Ez csak közelítőleg igaz, mert az eltérítőlemezek szélein fellépő inhomogenitás kis mértékben befolyásolja az eltérítéstől függően az érzékenységet.)

Statisztika:

28 dolgozat érkezett.
4 pontot kapott:	Bekes Barnabás, Endrész Balázs, Fekete Levente, Havasi Márton, Horváth 999 Anikó, Ludányi Levente, Nguyễn Đức Anh Quân, Pankotai Dóra Anna, Somlán Gellért, Szabados Noémi, Toronyi András, Török 517 Mihály.
3 pontot kapott:	Fiam Regina, Hartmann Alice, Horváth Antal, Kozák Gergely, Sas 202 Mór, Schäffer Bálint, Sepsi Csombor Márton, Tanner Norman, Vass Bence.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. februári fizika feladatai