 |
A P. 5214. feladat (2020. március) |
P. 5214. Ha a Torricelli-kísérletet a tengerszinten végezzük el, akkor az üvegcsőben 76 cm magasra emelkedik a higany. Egy igen magas hegyen azonban csak 40 cm-es higanyoszlop-magasságot mérünk. Mekkora függőleges erővel kell tartanunk az üvegcsövet a magas hegyen?
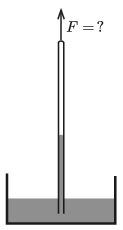
A cső belső átmérője 1 cm, teljes hossza 110 cm, ebből 10 cm merül a higanyba. A cső centiméterenként 1 g, fedőlapja pedig 5 g tömegű. (Az üveg sűrűsége 2,6 g/cm\(\displaystyle {}^3\).)
Közli: Honyek Gyula, Veresegyház
(5 pont)
A beküldési határidő 2020. április 14-én LEJÁRT.
Megoldás. Az üvegcső teljes súlya
\(\displaystyle G_1=\left(110~{\rm cm}\cdot 1\,\frac{\rm g}{\rm cm}+ 5~{\rm g}\right)\, 9{,}81~\frac{\rm N}{\rm kg}=1{,}13~\rm N.\)
A higanyoszlop (a higanyszint feletti rész) súlya:
\(\displaystyle G_2=\left(40~{\rm cm}\right)\cdot\left(0{,}5~{\rm cm}\right)^2\pi\cdot 13{,}6~\frac{\rm g}{\rm cm^3}\cdot 9{,}81~\frac{\rm N}{\rm kg}=4{,}19~\rm N.\)
Az üveg higanyba merülő, 10 cm hosszú részének térfogata \(\displaystyle V= \frac{10~\rm g}{2{,}6~{\rm g/cm}^3}=3{,}85~\rm cm^3\). Erre a csődarabra a higany által kifejtett felhajtóerő (a kiszorított higany súlya):
\(\displaystyle G_3=3{,}85~{\rm cm^3}\cdot 13{,}6~\frac{\rm g}{\rm cm^3}\cdot 9{,}81~\frac{\rm N}{\rm kg}=0{,}51~\rm N.\)
Az üvegcső egyensúlyban tartásához szükséges függőleges erő nagysága:
\(\displaystyle F=G_1+G_2-G_3=4{,}8~\rm N.\)
Statisztika:
28 dolgozat érkezett. 5 pontot kapott: Bekes Barnabás, Bokor Endre, Dóra Márton, Horváth 999 Anikó, Kertész Balázs, Ludányi Levente, Mócza Tamás István, Páhán Anita Dalma, Szabados Noémi, Szabó 314 László, Téglás Panna, Toronyi András, Török 111 László, Varga Vázsony, Vass Bence, Viczián Anna. 4 pontot kapott: Bonifert Balázs, Fekete András Albert. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. márciusi fizika feladatai
