A P. 5223. feladat (2020. április)

P. 5223. Vízszintes asztallapon az ábrán látható módon elhelyeztünk négy egyforma, egyenként 30 N súlyú golyót egy keretben, amely egy szabályos háromszög alapú hasáb. Mekkora erők hatnak az egyes érintkezési pontokban, ha a háromszög oldala 15 cm, a golyók átmérője pedig 5 cm? (A súrlódástól eltekinthetünk.)

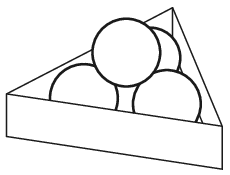
Közli: Németh László, Fonyód

(5 pont)

A beküldési határidő 2020. május 11-én LEJÁRT.

Megoldás. Tisztázzuk először a geometriai viszonyokat. Az 1. ábrán a négy golyó és a tartókeret felülnézeti képe látható.

1. ábra

Erről a nézetről leolvashatjuk, hogy a számunkra fontos távolságok (centiméter egységekben számolva) a következők: a háromszög oldalai \(\displaystyle AB=BC=CA=15;\) a háromszög magassága \(\displaystyle CD=AC\cdot \cos 30^\circ=12{,}99\); \(\displaystyle OC=\tfrac23 CD=8{,}66.\) Másrészt \(\displaystyle PC=5\) cm (ez a \(\displaystyle 30^\circ\)-os derékszögű háromszög megfelelő oldalainak arányából kapható meg), így \(\displaystyle OP=OC-PC=3{,}66\).

Nézzük most azt a vízszintes irányú, a \(\displaystyle CD\) egyenesre merőleges nézetet, amelyen a felső golyó és az egyik alsó golyó vetületi köre érinti egymást (2. ábra).

2. ábra

Ezen az ábrán feltüntettük a felső golyó és az egyik alsó golyó között ható, \(\displaystyle F_1\) nagyságú erőket, valamint a talaj által az alsó golyóra kifejtett \(\displaystyle F_2\) erőt is. A korábban kiszámított \(\displaystyle OP=3{,}66\)-ból és az egymást érintő gömbök középpontjának \(\displaystyle OO'=5\) távolságából megkapjuk, hogy az ábrán látható szög:

\(\displaystyle \alpha=\arccos \frac{3{,}66}{5{,}0}=42{,}9^\circ.\)

A felső golyó súlya és a három alsó golyó által kifejtett erők függőleges komponense egyensúlyt tart, tehát

\(\displaystyle 3F_1\sin\alpha=G=30~\rm N,\)

ahonnan \(\displaystyle F_1=14{,}7~\rm N.\)

Az egész rendszerre ható függőleges irányú eredője

\(\displaystyle 3F_2-4G=0,\)

vagyis \(\displaystyle F_2=40~\rm N\).

A 3. ábra ismét a függőleges irányú nézetet mutatja. A keret két oldala \(\displaystyle F_3\) nagyságú, vízszintes irányú erőt fejt ki a velük érintkező golyóra. Ezen erők eredője egyensúlyt tart az \(\displaystyle F_1\) erő vízszintes összetevőjével:

\(\displaystyle 2F_3\,\sin30^\circ=F_3=F_1\cos\alpha,\)

ahonnan \(\displaystyle F_3=10{,}7~\)N.

3. ábra

Statisztika:

20 dolgozat érkezett.
5 pontot kapott:	Bonifert Balázs, Fekete Levente, Kertész Balázs, Nguyễn Đức Anh Quân, Somlán Gellért, Szabó 314 László, Toronyi András, Tóth Ábel, Vakaris Klyvis, Varga Vázsony, Vass Bence, Viczián Anna.
4 pontot kapott:	Fekete András Albert, Páhán Anita Dalma, Sas 202 Mór, Téglás Panna.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.

A KöMaL 2020. áprilisi fizika feladatai