 |
A P. 5248. feladat (2020. szeptember) |
P. 5248. Egy \(\displaystyle 4\ell\) hosszúságú ellenálláshuzalt a két negyedelőpontjában derékszögben meghajlítottunk. Hol kell ehhez hozzákötni a \(\displaystyle 2\ell\) hosszúságú, ugyanebből a huzalból levágott vezetőt, ha azt akarjuk, hogy a huzalvégek között kialakuló eredő ellenállás megegyezzen egyetlen \(\displaystyle 2\ell\) hosszúságú vezető ellenállásával?
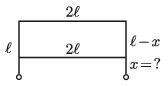
Példatári feladat nyomán
(4 pont)
A beküldési határidő 2020. október 15-én LEJÁRT.
Megoldás. Mindegyik vezetődarab ellenállása arányos a hosszával; az arányossági tényező legyen \(\displaystyle \varrho\). A sorosan és párhuzamosan kapcsolt ellenállások eredője a kapcsolás két végpontja között
\(\displaystyle \left(\frac{1}{4\ell\varrho -2x\varrho}+\frac{1}{2\ell\varrho}\right)^{-1}+2x\varrho=2\ell\varrho.\)
Innen algebrai átalakítások után az
\(\displaystyle x^2-3x\ell+\ell^2=0\)
másodfokú egyenletet kapjuk, amelynek a fizikailag értelmes (\(\displaystyle x<\ell\)) megoldása:
\(\displaystyle x=\left(1{,}5-\sqrt{1{,}25}\right)\ell\approx 0{,}38\,\ell.\)
Statisztika:
72 dolgozat érkezett. 4 pontot kapott: Antalóczy Szabolcs, Bognár 171 András Károly, Bonifert Balázs, Bubics Gergely Dániel, Csonka Illés, Dobre Zsombor, Domján Dorina, Dóra Márton, Dózsa Levente, Gurzó József, Hauber Henrik, Horváth 221 Zsóka, Horváth 999 Anikó, Jánosik Máté, Juhász Márk Hunor, Kertész Balázs, Koleszár Benedek, Koszta Benedek, Kovács Kinga, Kozaróczy Csaba, Ludányi Levente, Mihalik Bálint, Mócza Tamás István, Molnár 129 Anna, Mozolai Bende Bruno, Nemeskéri Dániel, Páhán Anita Dalma, Perényi Barnabás, Pogány Balázs, Puskás Attila, Sas 202 Mór, Schäffer Bálint, Schmercz Blanka, Somlán Gellért, Strinyi Péter, Surányi Blanka, Szoboszlai Szilveszter, Takács Bendegúz, Téglás Panna, Tóth Ábel, Varga Vázsony, Viczián Máté. 3 pontot kapott: 17 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. szeptemberi fizika feladatai
