A P. 5269. feladat (2020. november)

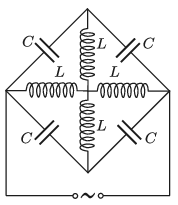
P. 5269. Mekkora frekvenciájú szinuszos váltóárammal szemben képvisel az ábrán látható összeállítás végtelen nagy ellenállást?

Példatári feladat nyomán

(5 pont)

A beküldési határidő 2020. december 15-én LEJÁRT.

Megoldás. A kapcsolás ,,függőleges'' szimmetriatengelyén fekvő három pont minden időpillanatban ekvipotenciális, hiszen a generátorhoz kapcsolódó pontoktól ,,egyforma távolságra'' helyezkednek el. (Ha mondjuk a bal oldali csomópontot földeltnek tekintjük, és a jobb oldali csomópont feszültsége \(\displaystyle U(t)\), akkor a három közbenső pont mindegyikén \(\displaystyle \tfrac12 U(t)\) feszültség lesz.) Az ekvipotenciális pontok közötti tekercsek eltávolíthatók a kapcsolásból (hiszen rajtuk úgysem folyik áram), a felső és alsó csomópont pedig összerköthető (hiszen közöttük nincs feszültség, emiatt úgysem fog áram folyni.)

Az átalakított kapcsolásban a párhuzamosan kapcsolt kondenzátorok eredője \(\displaystyle 2C\), a sorosan kapcsoltaké pedig \(\displaystyle \tfrac12\cdot 2C=C\). A két sorosan kapcsolt tekercs eredő önindukciós együtthatója \(\displaystyle 2L\). (Ez csak akkor igaz, ha a tekercsek nincsenek nagyon közel egymáshoz, és emiatt a kölcsönös indukció elhanyagolható.) A kapcsolás akkor képvisel ,,végtelen nagy'' váltóáramú ellenállást, amikor a körfrekvencia (a Thomson-képlet szerint)

\(\displaystyle \omega=2\pi f=\sqrt{\frac{1}{2L\cdot C}},\)

vagyis a rezonanciafrekvencia

\(\displaystyle f_\text{rez.}=\frac{1}{\pi}\sqrt{\frac{1}{8L\, C}}.\)

Statisztika:

14 dolgozat érkezett.
5 pontot kapott:	Bonifert Balázs, Gurzó József, Kertész Balázs, Sas 202 Mór, Schmercz Blanka, Selmi Bálint, Toronyi András.
4 pontot kapott:	Fekete András Albert, Varga Vázsony.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2020. novemberi fizika feladatai