 |
A P. 5314. feladat (2021. március) |
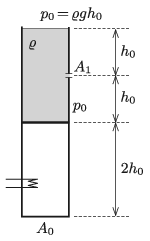
P. 5314. Egy függőleges, jól hőszigetelt, felül nyitott, \(\displaystyle A_0\) keresztmetszetű hengert két részre oszt egy szintén hőszigetelő anyagból készült, elhanyagolható vastagságú és tömegű dugattyú. A dugattyú alatti \(\displaystyle 2h_0\) magasságú térrészben levegő, míg felette \(\displaystyle 2h_0\) magasságban \(\displaystyle \varrho\) sűrűségű folyadék található. A dugattyú felett \(\displaystyle h_0\) magasságban a folyamat kezdetén megnyitunk egy apró, \(\displaystyle A_1\) keresztmetszetű nyílást, melyen a folyadék elkezd kifolyni a hengerből. A számítások során a légköri nyomás értékét vegyük \(\displaystyle p_0=\varrho gh_0\)-nak.
\(\displaystyle a)\) Hogyan változtassuk az elzárt levegőt melegítő fűtőszál teljesítményét az idő függvényében, hogy a folyadék állandó sebességgel folyjon ki a nyíláson?
\(\displaystyle b)\) Mennyi ideig tudjuk biztosítani a folyadék állandó sebességű kiáramlását, és ezen időpont után ez már miért nem oldható meg a fűtőszállal?
Közli: Olosz Balázs, Budapest
(6 pont)
A beküldési határidő 2021. április 15-én LEJÁRT.
Megoldás. A folyadék kiáramlási sebessége a lyuk feletti folyadékoszlop magasságától függ. Mivel a lyuk mérete kellően kicsi a henger alapterületéhez képest, kezdetben ez a kiáramlási sebesség:
\(\displaystyle v_0=\sqrt{2gh_0}.\)
A feladat szövege szerint úgy szeretnénk üzemeltetni a fűtőszálat, hogy ez a kiáramlási sebesség állandó értékű maradjon. Ez csak úgy lehetséges, ha a folyamat során nem változik a folyadékszint magassága a hengerben, vagyis a dugattyú annyival emeli meg a folyadékszintet, mint amennyivel az a kiáramlás miatt lesüllyedne. Ezt kihasználva fel lehet írni az elzárt levegő térfogat–idő függvényét. Egy rövid \(\displaystyle \Delta t\) idő alatt a kiáramló folyadék mennyisége:
\(\displaystyle \Delta V=A_1v_0\Delta t=A_1\sqrt{2gh_0}\Delta t.\)
Ha a folyadékszint magassága nem változik, akkor az elzárt levegőnek éppen ezzel az értékkel nő a térfogata. Mivel a térfogatváltozás állandó ütemű, így felírható a hengerben lévő levegő pillanatnyi térfogatának időbeli változása is:
\(\displaystyle V(t)=2h_0A_0+A_1\sqrt{2gh_0}t=A_0h_0\left(2+\frac{A_1}{A_0}\sqrt{\frac{2g}{h_0}}\,t\right).\)
Célszerű bevezetni a
\(\displaystyle V_0=A_0h_0\qquad \text{és} \qquad \frac{1}{t_0}=\frac{A_1}{A_0}\sqrt{\frac{2g}{h_0}}\)
jelöléseket. Ezekkel kifejezve a levegő térfogatának időbeli változását:
| \(\displaystyle (1)\) | \(\displaystyle V(t)=V_0\left(2+\frac{t}{t_0}\right).\) |
Ezek szemléletes jelentése:
\(\displaystyle V_0\) a kifolyónyílás feletti folyadékrész térfogata,
\(\displaystyle t_0\) az az idő, amennyi alatt az emelkedő dugattyú egyenletes mozgással elérné a kifolyónyílás szintjét.
A következő meghatározandó állapotjelző a levegő nyomása, annak időbeli változása. Mivel a dugattyú tömege elhanyagolható, így az egyensúlyának feltétele az, hogy a bezárt levegő nyomásából származó erő a felette elhelyezkedő folyadék hidrosztatikai nyomásával tartson egyensúlyt:
\(\displaystyle p(t)=p_0+\varrho g h(t),\)
ahol \(\displaystyle h(t)\) a folyadékoszlop pillanatnyi magassága. Ez a magasság a gáz térfogatának ismeretében így számolható:
\(\displaystyle h(t)=4h_0- \frac{{V(t)}}{A_0}.\)
A nyomás tehát
| \(\displaystyle (2) \) | \(\displaystyle p(t)=p_0\left(3-\frac{t}{t_0}\right).\) |
Megjegyzés. Ezt az eredményt úgy is megkaphatjuk, hogy meggondoljuk: kezdetben a gáz nyomása a külső légnyomás (\(\displaystyle p_0\)) és a \(\displaystyle 2h_0\) magas folyadékoszlop \(\displaystyle 2p_0\) hidrosztatikai nyomásának összege, tehát \(\displaystyle 3p_0\), továbbá az időben egyenletesen változó hidrosztatikai nyomás \(\displaystyle t_0\) idő alatt csökkenne \(\displaystyle p_0\)-lal.
\(\displaystyle a)\) Kicsiny \(\displaystyle \Delta t\) idő alatt a levegővel (melyre \(\displaystyle f=5\)) közlendő hő a hőtan első főtétele szerint:
\(\displaystyle \Delta Q=\frac{f}{2}\Delta (pV)+p\Delta V=\frac{7}{2}p\Delta V+\frac{5}{2}V\Delta p.\)
Az (1) és (2) összefüggések felhasználásával \(\displaystyle \Delta V=(V_0/t_0)\Delta t\), illetve \(\displaystyle \Delta p=-(p_0/t_0)\Delta t\). Ezek szerint a fűtőszál teljesítménye
\(\displaystyle P(t)=\frac{\Delta Q}{\Delta t}=\frac{p_0V_0}{2t_0}\left(11-12\frac{t}{t_0}\right).\)
Látjuk, hogy a fűtőszál teljesítményét időben egyenletesen csökkentenünk kell, ha az állandó kiáramlási sebességet fenn akarjuk tartani.
\(\displaystyle b)\) Azt is látjuk, hogy \(\displaystyle t^*=\frac{11}{12}t_0\) idő elteltével a teljesítmény már nullára csökken. A továbbiakban hűteni kellene a gázt, erre a fűtőszál nyilván nem képes, tehát a folyamat ,,megszalad''.
Megjegyzés. A továbbiakban a gáz állapotát a \(\displaystyle p-V\) diagramon szemléltető pont letér a lineáris szakaszról, és az adiabata mentén halad tovább. Anélkül, hogy hőt közölnénk a rendszerrel, a levegő térfogata nő, a nyomása és a hőmérséklete csökken. A nyomás csökkenése azonban nem olyan ütemű, mint amennyi a folyadékszint változatlan magasságban tartásához elegendő lenne, tehát a hengerben a folyadékszint ugrásszerűen emelkedni fog, a rendszer gejzírszerű viselkedésbe kezd.
Ellenőriznünk kell még, hogy \(\displaystyle t=t^*\) időpontig (vagy még előtte) nem éri-e el a dugattyú a kifolyónyílást. Mivel \(\displaystyle t^*<t_0\),
\(\displaystyle V(t^*)=\left(2+\frac{11}{12}\right)V_0\approx 2{,}92\,V_0<3\,V_0,\)
a dugattyú még éppen a kifolyónyílás alatt maradt. Érdekes, hogy a \(\displaystyle p(t)\cdot V(t)\)-vel arányos hőmérséklet a melegítés során a \(\displaystyle t=\tfrac12 t_0\) időpillanatban éri el a maximális értékét, ettől kezdve a levegő – jóllehet a fűtőszállal fűtjük – hűl!
Statisztika:
17 dolgozat érkezett. 6 pontot kapott: Kertész Balázs, Somlán Gellért, Téglás Panna, Toronyi András. 5 pontot kapott: Fekete András Albert, Gurzó József, Selmi Bálint. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. márciusi fizika feladatai
