A P. 5344. feladat (2021. szeptember)

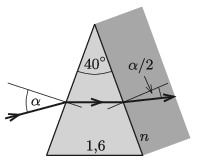
P. 5344. Egyenlő szárú háromszög keresztmetszetű prizma törőszöge \(\displaystyle 40^\circ\), anyagának törésmutatója 1,6. Mekkora \(\displaystyle \alpha\) beesési szöggel érkezik a fénysugár az egyik oldallaphoz, ha ez a fénysugár a prizmában az alappal párhuzamosan halad tovább? Mekkora \(\displaystyle n\) törésmutatója van annak az üvegnek, amiből készült hasábot a prizma másik oldalához illesztve a törési szög az ábra szerint \(\displaystyle \alpha/2\)?

Közli: Kobzos Ferenc, Dunaújváros

(4 pont)

A beküldési határidő 2021. október 15-én LEJÁRT.

Megoldás. A prizmába belépő fény törési szöge \(\displaystyle \beta=20^\circ\), így a beesési szög szinusza:

\(\displaystyle \sin\alpha=n_\text{prizma}\cdot \sin20^\circ=0{,}547, \qquad \alpha=33{,}2^\circ.\)

Ha a prizmából kilépő fény törési szöge \(\displaystyle 16{,}6^\circ\), akkor a prizma és a hozzá illesztett üveg relatív törésmutatója:

\(\displaystyle \frac{1{,}6}{n}=\frac{\sin 16{,}6^\circ}{\sin 20^\circ}=0{,}835,\)

azaz a keresett törésmutató:

\(\displaystyle n=\frac{1{,}6}{0{,}835}\approx1{,}92.\)

Statisztika:

55 dolgozat érkezett.
4 pontot kapott:	Bagu Bálint, Antalóczy Szabolcs, Beke Bálint, Bencz Benedek, Biebel Botond, Bogdán Benedek, Brezina Gergely, Csonka Illés, Dóra Márton, Elekes Dorottya, Füles Ferenc, Hegedűs Máté Miklós, Jirkovszky-Bari László, Katona Attila Zoltán, Kovács Kinga, Mihályi Gábor, Miruna Neacsu, Molnár Kristóf, Mozolai Bende Bruno, Papp Marcell Imre, Pethő Dorottya, Radvánszki Ferenc, Rahimkulov Margarita, Schneider Dávid, Somlán Gellért, Sulok Yahyaa, Szabó Márton, Szabó Milán Bogdán, Tárnok Ede , Tatár Ágoston, Téglás Panna, Török Dorka, Vágó Botond, Varga Mária Krisztina, Veszprémi Rebeka Barbara, Vig Zsófia, Vincze Farkas Csongor.
3 pontot kapott:	Boda Benedek János, Dobre Zsombor, Magyar Gábor Balázs, Marozsi Lenke Sára.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. szeptemberi fizika feladatai