 |
A P. 5403. feladat (2022. április) |
P. 5403. Valaki egy olyan mobilgát építését javasolta, ami egy vízszintes és hozzá \(\displaystyle 45^\circ\)-os szögben csatlakozó vaslapból áll. A két fémlapnak a közös élre merőleges mérete 1 méter, illetve \(\displaystyle \sqrt2\) méter, a fémlapok vastagsága 2 cm. ,,Ezt a szerkezetet nemcsak a vaslapok súlya, de még a víz nyomása is a talajhoz szorítja'' – érvelt a feltaláló.
\(\displaystyle a)\) Legalább mekkora (tapadási) súrlódási együtthatóra van szükség a mobilgát és a talaj között, hogy a védelem még a maximális vízmagasság esetén is biztonságos legyen?
\(\displaystyle b)\) Hol lehet az ilyen alakú mobilgátakon a talaj által kifejtett függőleges nyomóerő támadáspontja, ha 2 cm-nél vastagabb, vagy vékonyabb vaslapot alkalmazunk? Felborulhat-e a mobilgát a legmagasabb vízállásnál (vagyis amikor a víz éppen a ferde vaslap tetejéig ér)?
Vizsgáljuk meg a mobilgát elhelyezésének kétféle lehetőségét:
\(\displaystyle (i)\) a ferde felület a víz felé dől;
\(\displaystyle (ii)\) a ferde felület a védendő terület felé dől.
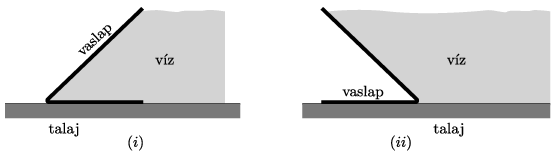
Közli: Simon Péter, Pécs
(5 pont)
A beküldési határidő 2022. május 16-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Jelöljük a mobilgát 1 méter hosszú szakaszának tömegét \(\displaystyle M\)-mel, a ferde rész alatti, illetve feletti víz tömegét pedig \(\displaystyle m\)-mel, a fémlap vastagságát \(\displaystyle d\)-vel, a vízszint legnagyobb magasságát \(\displaystyle \ell\)-lel (ami megegyezik a mobilgát talajon fekvő részének szélességével).
A megadott adatokból és az ismert anyagi állandókból kiszámíthatjuk, hogy
\(\displaystyle M=(1+\sqrt2)\ell d \varrho_\text{vas}\cdot \text{(1 méter)}=2{,}41\cdot 0{,}02\cdot 7860\ {\rm kg}\approx 380\ \rm kg,\)
\(\displaystyle m=\frac12 \ell^2\varrho_\text{víz}\cdot \text{(1 méter)}=500\ \rm kg.\)
Az ábrán a vaslemezre ható erőket ábrázoltuk, a talaj nyomóerejét \(\displaystyle N\)-nel, a súrlódási erőt pedig \(\displaystyle S\)-sel jelöltük.
\(\displaystyle (i)\) eset. A víz függőleges irányban összesen \(\displaystyle mg\) erőt fejt ki a mobilgátra. A vízszintes vaslapra ható, a víz nyomásából származó erő \(\displaystyle 2mg\) (hidrosztatikai paradoxon), tehát a ferde lapra a víz függőlegesen \(\displaystyle mg\) erőt kell, hogy kifejtsen. De mivel a ferde lapra ható eredő erő a \(\displaystyle 45^\circ\)-os szögben álló vaslapra merőleges, ennek az erőnek a vízszintes komponense is \(\displaystyle mg\). A vízszintes és a függőleges erők egyensúlyából következik, hogy
\(\displaystyle S=mg, \qquad \text{továbbá} \qquad N=Mg+mg.\)
Mivel \(\displaystyle S\le \mu N,\) a súrlódási együttható legkisebb értéke (ami mellett még nem csúszik meg a gát):
\(\displaystyle \mu_\text{min}=\frac{S}{N}=\frac{m}{m+M}\approx \frac{500}{500+380}=0{,}57.\)

\(\displaystyle (ii)\) eset. A víz most is ugyanolyan nyomással hat a ferde lapra, viszont a víz nyomásából származó erő nem ,,emeli'', hanem ,,leszorítja'' a ferde lapot. A lapra merőleges nyomóerőnek mind a függőleges, mind a vízszintes összetevője \(\displaystyle mg\), a vízszintes lemezre viszont nem hat a hidrosztatikai nyomás, hiszen közvetlenül felette nincs is víz. Most is igaz, hogy \(\displaystyle S=mg\) és \(\displaystyle N=Mg+mg.\) A súrlódási együttható legkisebb értéke ugyanakkora, mint az előző esetben: \(\displaystyle \mu_\text{min}\approx 0{,}57.\)
Megjegyzés. Ilyen nagy súrlódás a nedves, felázott talaj és a vaslap között aligha létezik. A ténylegesen megépített, hasonló szerkezetű mobilgátaknál a vízszintes vaslapból függőleges ,,tüskék'' nyúlnak ki, és ezek a talajba mélyedve megakadályozzák a gát elcsúszását.
\(\displaystyle b)\) Számítsuk ki az \(\displaystyle N\) erő hatásvonalának a vaslapok törésvonalától mért \(\displaystyle x\) távolságát. Felhasználjuk, hogy a folyadék hidrosztatikai nyomásából származó eredő erő támadáspontja a folyadék alsó egyharmadánál van.
A mobilgátra ható erők forgatónyomatékának egyensúlyából megkaphatjuk \(\displaystyle x\) értékét. A gát feldőlés szempontjából akkor stabil, ha \(\displaystyle 0<x<\ell\).
Az \(\displaystyle (i)\) esetben fennáll, hogy
\(\displaystyle x(mg+Mg) +\frac{\ell}3mg +\frac{\ell}3mg=\frac{\ell}2(2m+M)g,\)
vagyis
\(\displaystyle x=\frac{\frac12 +\frac{m}{3M}}{1+\frac{m}{M} }\ell\approx 0{,}4\ \rm m.\)
Ez a távolság más vastagságú vaslemez (tehát más \(\displaystyle M\) tömeg, vagyis más \(\displaystyle \frac{m}{M}\) arány) esetén biztosan \(\displaystyle \frac13\ell\) és \(\displaystyle \frac12\ell\) közé esik, tehát a gát nem borulhat fel.
A \(\displaystyle (ii)\) esetben felírhatjuk, hogy
\(\displaystyle x(mg+Mg) -\frac{\ell}3mg -\frac{\ell}3mg=\frac{\ell}2Mg,\)
ahonnan
\(\displaystyle x=\frac{\frac12 +\frac{2m}{3M}}{1+\frac{m}{M} }\ell\approx 0{,}6\ \rm m.\)
Tetszőleges tömegarány mellett érvényes, hogy
\(\displaystyle \frac12\ell<x<\frac23\ell,\)
tehát a gát ebben az esetben sem borulhat fel.
Statisztika:
12 dolgozat érkezett. 5 pontot kapott: Gábriel Tamás, Kertész Balázs, Téglás Panna, Toronyi András, Vig Zsófia, Waldhauser Miklós. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2022. áprilisi fizika feladatai
