 |
A P. 5408. feladat (2022. április) |
P. 5408. A vízszintes felületen lévő, tartóoszloppal rendelkező, \(\displaystyle M = 3m\) tömegű kiskocsira egy fonálingát szerelünk. Az inga hossza \(\displaystyle L = 50\) cm, a végén lévő, pontszerűnek tekinthető golyó tömege \(\displaystyle m = 0{,}15\) kg. Kezdetben a testek nyugalomban vannak. Az ingát a fonál feszes állapotában vízszintes helyzetéig kitérítjük, és kezdősebesség nélkül elengedjük. A súrlódás mindenhol elhanyagolható.
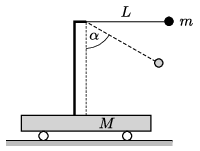
\(\displaystyle a)\) Mekkora a kocsi sebessége, amikor a fonál \(\displaystyle \alpha = 60^\circ\)-os szöget zár be a függőleges iránnyal?
\(\displaystyle b)\) Mekkora erő feszíti ekkor a fonalat?
Közli: Kotek László, Pécs
(6 pont)
A beküldési határidő 2022. május 16-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Legyen az \(\displaystyle m\) tömegű golyó talajhoz viszonyított sebességének vízszintes komponense a kérdéses pillanatban \(\displaystyle v_1\), függőleges komponense pedig \(\displaystyle v_2\) (1. ábra). Haladjon ugyanekkor a kocsi \(\displaystyle u\) sebességgel.

1. ábra
A rendszerre nem hat vízszintes irányú külső erő, ezért a vízszintes irányú lendület mindvégig nulla marad. Eszerint
| \(\displaystyle (1)\) | \(\displaystyle 3mu=mv_1, \qquad \text{azaz}\qquad v_1=3u.\) |
A mechanikai energia megmaradásásak törvénye szerint
\(\displaystyle mgL\cos\alpha=\frac12 m\left(v_1^2+v_2^2\right)+\frac12\,(3m)\,u^2,\)
vagyis (1) felhasználásával
| \(\displaystyle (2)\) | \(\displaystyle gL=v_2^2+12 u^2.\) |
Az \(\displaystyle m\) tömegű golyó az \(\displaystyle u\) sebességgel mozgó kiskocsihoz képest körpályán mozog. A fonál hosszának állandóságát kifejező kényszerfeltétel miatt:
\(\displaystyle \frac{v_2}{v_1+u}=\frac{v_2}{4u}={\rm tg}\,\alpha=\sqrt{3},\)
vagyis
| \(\displaystyle (3)\) | \(\displaystyle v_2=4\sqrt{3}\,u.\) |
Ezt (2)-be helyettesítve kapjuk, hogy a kiskocsi sebessége
\(\displaystyle u=\sqrt{\frac{gL}{60}}=0{,}28\ \frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) Legyen a fonalat feszítő erő \(\displaystyle K\), a kiskocsi gyorsulása pedig \(\displaystyle a\) (2. ábra). A kiskocsi mozgásegyenlete:
\(\displaystyle K\sin\alpha=Ma=3m\,a,\qquad \text{vagyis}\qquad ma=\frac{1}{3}K\sin\alpha. \)

2. ábra
A golyónak a kiskocsihoz viszonyított sebessége az energiatétel szerint (az első rész megoldásánál használt jelöléseket követve):
\(\displaystyle v_\text{rel}=\sqrt{(u+v_1)^2+v_2^2}=\sqrt{(4u)^2+\left(4\sqrt{3}u\right)^2}=8u=\sqrt{\frac{16}{15}\,gL}.\)
Ezen relatív sebesség miatt a golyónak
\(\displaystyle a_\text{cp}=\frac{v_\text{rel}^2}{L}= \frac{16}{15}\,g\)
nagyságú, fonál irányú centripetális gyorsulása van. Ehhez járul még a kiskocsi \(\displaystyle a\) nagyságú, vízszintes irányú gyorsulásának fonál irányú komponense, ami \(\displaystyle -a\sin\alpha\). A fonál irányú mozgásegyenlet:
\(\displaystyle K-mg\cos\alpha=m\left(a_\text{cp}-a\sin\alpha\right),\)
amiből az \(\displaystyle a\)-ra és \(\displaystyle a_\text{cp}\)-ra vonatkozó összefüggések behelyettesítése után megkapjuk a fonalat feszítő erőt:
\(\displaystyle K=\frac{mg\cos\alpha+\frac{16}{15}\,mg}{1+\frac{1}{3}\sin^2\alpha}=\frac{94}{75}\,mg=1{,}84\ \rm N.\)
Statisztika:
22 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Dóra Márton, Gábriel Tamás, Kürti Gergely, Molnár Kristóf, Somlán Gellért, Toronyi András. 5 pontot kapott: Horváth 221 Zsóka, Kertész Balázs, Nagy 456 Imre. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. áprilisi fizika feladatai
