A P. 5420. feladat (2022. szeptember)

P. 5420. \(\displaystyle a)\) Milyen \(\displaystyle \alpha\) szög esetén van egyensúlyban az ábrán látható rendszer, ha a lejtőn nincs súrlódás?

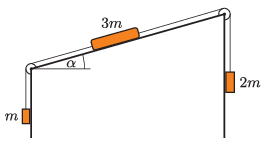
\(\displaystyle b)\) Milyen \(\displaystyle \alpha\) szögek esetén vannak egyensúlyban a testek, ha a lejtőn a súrlódási együttható \(\displaystyle \mu = 0{,}2\)?

\(\displaystyle c)\) Mekkora gyorsulással és merre mozognak a testek, ha \(\displaystyle \alpha=35^\circ\) és a súrlódási együttható \(\displaystyle \mu= 0{,}15\)? Mekkora ebben az esetben a két kötélerő aránya?

Közli: Siposs András, Budapest

(5 pont)

A beküldési határidő 2022. október 17-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Egyensúly esetén a kötelekben \(\displaystyle mg\), illetve \(\displaystyle 2mg\) erő hat, a lejtőn fekvő testre pedig lejtőirányban lefelé \(\displaystyle 3mg\,\sin\alpha \). A rendszer akkor van egyensúlyban, ha

\(\displaystyle mg+3mg\sin \alpha = 2mg,\)

vagyis \(\displaystyle \sin\alpha=\frac13\), tehát \(\displaystyle \alpha\approx 19{,}5^\circ\).

\(\displaystyle b)\) Az imént kapottnál nagyobb szög esetén (tehát ha \(\displaystyle \sin\alpha>\frac13\)) a lejtőn lévő test balra fog lecsúszni, vagy nyugalomban marad. Ha pedig \(\displaystyle \sin\alpha<\frac13\), akkor jobbra fog mozogni a \(\displaystyle 3m\) tömegű test, vagy nyugalomban marad. A nyugalom feltétele az, hogy a testet mozgatni akaró erő abszolút értéke kisebb legyen, mint a súrlódási erő maximális értéke, ami \(\displaystyle 3mg\mu\cos\alpha\):

\(\displaystyle \vert mg(3\sin\alpha- 1 )\vert< 3\cdot 0{,}2\,mg\cos\alpha.\)

Négyzetre emelés és rendezés után \(\displaystyle \sin\alpha\)-re egy másodfokú egyenlőtlenséget kapunk:

\(\displaystyle 9{,}36\sin^2\alpha - 6\sin\alpha +0{,}64 < 0,\)

aminek megoldása:

\(\displaystyle 0{,}135 < \sin\alpha < 0{,}506, \qquad \text{azaz}\qquad 7{,}8^\circ<\alpha<30{,}4^\circ.\)

\(\displaystyle c)\) Ekkora szögnél és ekkora súrlódás esetén a \(\displaystyle 3m\) tömegű test biztosan balra fog mozogni, hiszen – mint a \(\displaystyle b)\) kérdésre adott válasznál láttuk – még nagyobb (\(\displaystyle \mu=0{,}2\)-es) súrlódási együttható esetén is \(\displaystyle 30{,}4^\circ\)-nál meredekebb lejtőn nem maradhat egyensúlyban a rendszer.

Jelöljük a bal oldali kötelet feszítő erőt \(\displaystyle K_1\)-gyel, a másik kötélben ébredő erőt pedig \(\displaystyle K_2\)-vel. A mozgásegyenletek:

\(\displaystyle mg-K_1 = ma,\)

\(\displaystyle K_2-2mg = 2ma,\)

\(\displaystyle K_1+3mg(\sin\alpha -\mu \cos\alpha )-K_2 = 3ma.\)

A három egyenlet összegéből kapjuk, hogy

\(\displaystyle a=\left(\frac12\sin 35^\circ - \frac12\,0{,}15\cos 35^\circ -\frac{1}{6}\right)g=0{,}059\,g= 0{,}58~\frac{\rm m}{\rm s^2}.\)

A köteleket feszítő erők az \(\displaystyle m\) és a \(\displaystyle 2m\) tömegű test mozgásegyenlete szerint:

\(\displaystyle K_1=m(g-a)=0{,}94\,mg \qquad \text{és}\qquad K_2=2m(g+a)=2{,}12\,mg, \)

az arányuk pedig

\(\displaystyle \frac{K_2}{K_1}\approx 2{,}25.\)

Statisztika:

96 dolgozat érkezett.
5 pontot kapott:	Fórizs Borbála, Kismárton Gábor, Seprődi Barnabás Bendegúz, Vágó Botond, Vincze Farkas Csongor.
4 pontot kapott:	Arnold Lőrinc, Baranyi Bartal, Beke Bálint, Beke Botond, Bencz Benedek, Benes András, Bocor Gergely, Bodré Zalán, Bunford Luca, Chrobák Gergő, Csernyik Péter, Csiszár András, Csonka Illés, Elekes Dorottya, Fitos Gergő, Görcsös Ákos Attila, Halász Henrik, Hegedűs Máté Miklós, Katona Attila Zoltán, Klement Tamás, Kondor Botond Dávid, Márfai Dóra, Masa Barnabás, Molnár Kristóf, Nagy 456 Imre, Nemeskéri Dániel, Osváth Emese, Petró Péter, Richlik Márton, Schmercz Blanka, Szabó Márton, Tárnok Ede , Tatár Ágoston, Waldhauser Miklós, Wodala Gréta Klára.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	17 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2022. szeptemberi fizika feladatai