 |
A P. 5422. feladat (2022. szeptember) |
P. 5422. Egy zárt, henger alakú, \(\displaystyle L=40\) cm hosszúságú, hővezető falú tartályt egy vékony dugattyú oszt két részre, amelyekben ideálisnak tekinthető gáz található. Kezdetben a tartály tengelye függőleges, a dugattyú pedig egyensúlyi állapotában éppen a tartály felénél helyezkedik el. Ezután a tartály szimmetriatengelyét \(\displaystyle 90^\circ\)-kal lassan elforgatjuk, melynek eredményeképp a dugattyú \(\displaystyle 10\) cm távolsággal mozdul el. Mennyivel mozdult volna el a dugattyú, ha \(\displaystyle 90^\circ\) helyett \(\displaystyle 180^\circ\)-kal forgattuk volna el a tartályt? A hőmérséklet mindvégig állandó.
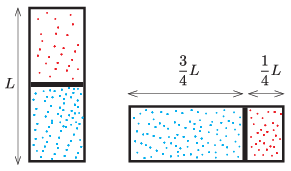
Példatári feladat nyomán
(4 pont)
A beküldési határidő 2022. október 17-én LEJÁRT.
Megoldás. Jelöljük a dugattyúra ható nehézségi erőt \(\displaystyle G\)-vel, a dugattyú keresztmetszetét \(\displaystyle A\)-val, a közös hőmérsékletet pedig \(\displaystyle T\)-vel. Legyen a kezdetben felül lévő gáz mólszáma \(\displaystyle n_1\), az alsó részben lévő gáz mólszáma \(\displaystyle n_2\). A \(\displaystyle pV=nRT\) gáztörvény szerint a dugattyú mechanikai egyensúlyának feltétele a kezdeti helyzetben:
| \(\displaystyle (1)\) | \(\displaystyle n_2\frac{RT}{\frac12LA}=n_1\frac{RT}{\frac12LA}+\frac{G}{A},\) |
a \(\displaystyle 90^\circ\)-kal elforgatott helyzetben pedig
| \(\displaystyle (2)\) | \(\displaystyle n_2\frac{RT}{\frac34LA}=n_1\frac{RT}{\frac14LA},\qquad \text{ahonnan}\qquad n_2=3n_1.\) |
Végül pedig a \(\displaystyle 180^\circ\)-kal elforgatott helyzetben (ha a dugattyú elmozdulását \(\displaystyle xL\)-lel jelöljük):
| \(\displaystyle (3)\) | \(\displaystyle n_1\frac{RT}{\left(\frac12-x\right)LA}=n_2\frac{RT}{\left(\frac12+x\right)LA}+\frac{G}{A}.\) |
(2)-t (1)-be és (3)-ba helyettesítve, majd a két egyenletet kivonva egymásból az
\(\displaystyle \frac1{\frac12-x}=\frac3{\frac12+x}+4\)
egyenletet kapjuk, amelyből a
\(\displaystyle 2x^2+2x-1=0\)
másodfokú egyenlet következik. Ennek nemnegatív gyöke:
\(\displaystyle x=\frac{\sqrt{3}-1}{2}\approx 0{,}37,\)
a dugattyú elmozdulása tehát \(\displaystyle xL=14{,}6~\rm cm.\)
Statisztika:
65 dolgozat érkezett. 4 pontot kapott: Arnold Lőrinc, Beke Bálint, Bernhardt Dávid, Bogdán Benedek, Brezina Gergely, Bunford Luca, Chrobák Gergő, Csonka Illés, Fajszi Karsa, Fehérvári Donát, Flóring Balázs, Fórizs Borbála, Glaser Dávid, Hegedűs Máté Miklós, Katona Attila Zoltán, Klement Tamás, Kovács Barnabás, Kozma Bertalan, Lévai Dominik Márk, Lincoln Liu, Mészáros Ádám, Molnár Kristóf, Molnár Zétény, Nagy 456 Imre, Osváth Emese, Péntek Domonkos, Schmercz Blanka, Seprődi Barnabás Bendegúz, Seprődi Lili Borbála, Tóth Kolos Barnabás, Török Hanga, Vig Zsófia, Waldhauser Miklós. 3 pontot kapott: Beke Botond, Csóka Péter, Elekes Dorottya, Görcsös Ákos Attila, Nemeskéri Dániel, Richlik Márton, Tomesz László Gergő. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2022. szeptemberi fizika feladatai
