 |
A P. 5423. feladat (2022. szeptember) |
P. 5423. Egy hosszú, egyenes vezetőre merőleges síkban egy téglalap alakú drótkeretet helyezünk el. A vezetőhöz legközelebb, \(\displaystyle d\) távolságra a keret egyik élének középpontja található. Vonzza vagy taszítja egymást a két vezeték, ha az egyenes vezetőben \(\displaystyle I_1\), a vezető keretben pedig \(\displaystyle I_2\) erősségű áram folyik?
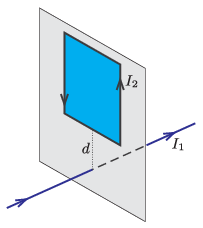
Példatári feladat nyomán
(4 pont)
A beküldési határidő 2022. október 17-én LEJÁRT.
I. megoldás. Forgassuk körbe – gondolatban – a drótkeretet az egyenes vezetőre merőleges felezővonala körül. Abban a helyzetben, amikor a drótkeret alsó oldala párhuzamos az egyenes vezetővel és a közelebb folyó áramok egyirányúak, akkor (az Ampère-törvény és a Lorentz-erő képlete szerint) vonzóerő, ehhez képest \(\displaystyle 180^\circ\)-kal elforgatott helyzetben viszont taszítóerő lép fel. Az elfordulás szögét folyamatosan változtatva lesz egy olyan helyzet, amikor az erő nulla, és az elrendezés szimmetriája miatt ez éppen a feladatban szereplő ,,merőleges'' helyzetben következik be.
II. megoldás. A hosszú egyenes vezető mágneses tere hengerszimmetrikus, a vezető keret alakja pedig tükörszimmetrikus a téglalap azon felezővonalára nézve, amely merőleges az egyenes vezetőre. A vezető keret egyes kis darabjaira ható erő a Lorentz-féle \(\displaystyle \Delta F=BI\cdot \Delta \ell\) összefüggés és a jobbkéz-szabály alapján számítható, az eredő erő pedig ezek vektori összegeként áll elő.
A fentiek szerint a drótkeret két-két, egymással tükörszimmetrikusan elhelyezkedő kis darabkájára ható erők ugyanakkora nagyságúak, de ellentétes irányúak, összegük tehát páronként nulla, emiatt a teljes drótkeretre számított eredő erő is eltűnik. Az egész drótkeret és az egyenes vezető tehát se nem vonzza, se nem taszítja egymást.
Statisztika:
12 dolgozat érkezett. 3 pontot kapott: Ferencz Kamilla, Hüvös Gergely, Lincoln Liu. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2022. szeptemberi fizika feladatai
