 |
A P. 5427. feladat (2022. október) |
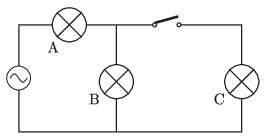
P. 5427. Az ábrán látható áramkörben található 230 V névleges feszültségű volfrámszálas izzólámpák egyformák, melyeknek áram–feszültség karakterisztikáját az alábbi grafikon mutatja. Az áramkörben található feszültségforrás 230 V-os.
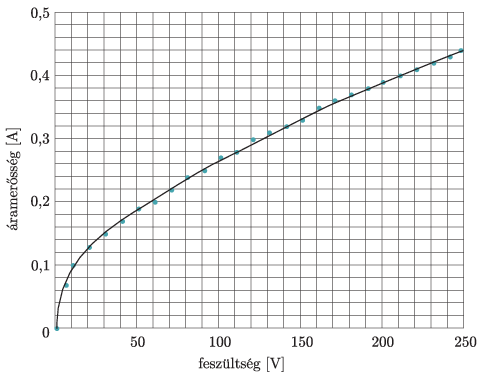
100 W-os villanykörte áram–feszültség karakterisztikája
\(\displaystyle a)\) Mekkora egy ilyen izzólámpa elektromos ellenállása a névleges feszültségen?
\(\displaystyle b)\) Mekkora ellenállású az A és a B lámpa izzószála a kapcsoló nyitott állásában?
\(\displaystyle c)\) Mekkora ellenállásúak az izzószálak a kapcsoló zárása után?
\(\displaystyle d)\) Mekkora teljesítményt adnak le az izzólámpák a fenti esetekben?
Közli: Honyek Gyula, Veresegyház
(5 pont)
A beküldési határidő 2022. november 15-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A grafikonról leolvashatjuk, hogy 230 V feszültségnél az áramerősség 0,42 A, az izzó ellenállása tehát
\(\displaystyle R=\frac{230~\rm V}{0{,}42~\rm A}=548~\Omega.\)
\(\displaystyle b)\) Nyitott kapcsolóállásnál az A és a B izzó feszültsége azonos, mivel azonos erősségű áram folyik rajtuk keresztül, így
\(\displaystyle U_{\rm A}^{\rm (ny)}=U_{\rm B}^{\rm (ny )}=115~V.\)
Az áramerősség tehát (lásd a grafikont)
\(\displaystyle I_{\rm A}^{\rm (ny)}=B_{\rm B}^{\rm (ny )}=0{,}285~\rm A,\)
így az ellenállásuk:
\(\displaystyle R_{\rm A}^{\rm (ny)}=R_{\rm B}^{\rm (ny)}=\frac{115~\rm V}{0{,}285~\rm A}\approx 404~\Omega.\)
\(\displaystyle c)\) Ha zárt kapcsolóállásnál a B, illetve a C izzón \(\displaystyle I\), az A izzón pedig \(\displaystyle 2I\) erősségű áram folyik, akkor a grafikusan megadott \(\displaystyle U(I)\) karakterisztika szerint fennáll:
\(\displaystyle U(I)+U(2I)=230~\rm V.\)
Ezt az egyenletet próbálgatással, különböző \(\displaystyle I\) értékek behelyettesítésével oldhatjuk meg. Azt kapjuk, hogy \(\displaystyle I\approx 0{,}37~\rm A\), vagyis
\(\displaystyle I_{\rm A}^{\rm (z)} =2I=0{,}185~{\rm A}, \qquad I_{\rm B}^{\text(z)}=I_{\rm C}^{\rm (z)}=I=0{,}185~{\rm A},\)
és az izzókra jutó feszültség:
\(\displaystyle U_{\rm A}^{\rm (z)}=U(2I)\approx 183~{\rm V}, \qquad U_{\rm B}^{\rm (z)}=U_{\rm C}{\rm (z)}=U(I)\approx 47~\rm V.\)
Természetesen teljesül, hogy \(\displaystyle U_{\rm A}^{\rm (z)}+U_{\rm B}^{\rm (z)}=230~\rm V.\)
\(\displaystyle d)\) Az izzók teljesítménye a megfelelő feszültség és áramerősség szorzata.
– Egyetlen, 230V-ra kapcsolt villanykörte teljesítménye:
\(\displaystyle P=(230~{\rm V})\cdot (0{,}42~{\rm A})\approx 97~\rm W,\)
ami egy kicsit kisebb a megadott ,,névleges'' teljesítménynél.
– Hasonlóan kapjuk, hogy nyitott kapcsolóállásnál
\(\displaystyle P_{\rm A}^{\rm (ny)}=P_{\rm B}^{\rm (ny)}\approx 33~\rm W.\)
– Ha zárjuk a kapcsolót, az izzók teljesítménye:
\(\displaystyle P_{\rm A}^\text{(z)}=U_{\rm A}^{\rm (z)}\cdot I_{\rm A}^{\rm (z)}\approx 67~{\rm W}, \qquad P_{\rm B}^{\rm (z)}=P_{\rm C}^{\rm (z)}==U_{\rm B}^{\rm (z)}\cdot I_{\rm BA}^{\rm (z)}\approx9~\rm W.\)
Látható, hogy a kapcsoló zárásával az A izzó fényesebben világít, B teljesítménye pedig olyan erősen lecsökken, hogy gyakorlatilag nem is fog világítani. Ezek a változások ugyanolyan jellegűek, de lényegesen nagyobb mértékűek, mint a hőfokfüggetlen ellenállású fogyasztóknál (lásd a G. 792. gyakorlat megoldását). Az izzók feszültség-áram karakterisztikájának nemlinearitását az ellenállás hőfokfüggése okozza.
Statisztika:
44 dolgozat érkezett. 5 pontot kapott: Bencz Benedek, Bernhardt Dávid, Csiszár András, Dancsák Dénes, Dér Levente, Flóring Balázs, Halász Sámuel, Klement Tamás, Kovács Kristóf , Lévai Dominik Márk, Márfai Dóra, Molnár Kristóf, Nemeskéri Dániel, Novák Péter, Osváth Emese, Schmercz Blanka, Sipeki Árpád, Szabó Imre Bence, Tomesz László Gergő, Tóth Kolos Barnabás, Vincze Farkas Csongor. 4 pontot kapott: Chrobák Gergő, Dercsényi Bence, Harkai Barnabás, Nagy 333 Zalán, Sándor Dominik, Szatmári András Gábor, Tárnok Ede , Vágó Botond, Varga 451 Erik, Vásárhelyi István Péter. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2022. októberi fizika feladatai
