 |
A P. 5433. feladat (2022. október) |
P. 5433. Egy vízzel töltött, téglatest alakú, elhanyagolható falvastagságú akvárium három függőleges oldala a vízből rájuk eső fényt visszaveri. Az akvárium szélessége \(\displaystyle d = 50\) cm, hossza \(\displaystyle L=120\) cm. Az akvárium rövidebb oldalához vízszintes síkban valamekkora beesési szögben lézersugár érkezik. Az ábra felülnézetet mutat. (A víz törésmutatója: \(\displaystyle n=4/3\).)
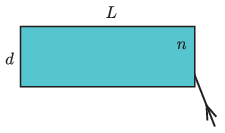
A kilépő fénysugár – többszöri tükröződés után – éppen a beeső fénysugárral párhuzamosan haladva hagyja el az akváriumot. Legfeljebb hány tükröződés történhetett?
Zsigri Ferenc (Budapest) feladata nyomán
(5 pont)
A beküldési határidő 2022. november 15-én LEJÁRT.
Megoldás. A fény \(\displaystyle \alpha\) beesési szög esetén
\(\displaystyle \beta=\arcsin\frac{\sin\alpha}{n}\)
szögtben halad tovább a vízben. Mivel \(\displaystyle \sin\alpha<1,\)
\(\displaystyle \beta<\arcsin\frac34=48{,}6^\circ.\)
A törés után a fénysugár többször tükröződhet az akvárium hosszabb oldalfalain és egyszer a rövidebben. Ha tükrözzük az akvárium felülnézeti ábráját az oldalfalakra és a hátsó falára, a fénysugár útja egyenessé válik (lásd az ábrát).

Tegyük fel, hogy mire a fénysugár visszaérkezik az akvárium tükrözésmentes falához (az ábrán a bal szélső egyeneshez), a hosszabb oldalakon \(\displaystyle k\)-szor verődik vissza. Amennyiben \(\displaystyle k\) páratlan szám, a másodszor is megtörő fénysugár az eredetivel párhuzamosan halad a levegőben. Ez a feltétel akkor teljesül, ha a fény az ábrán halványszürkén jelölt sávok valamelyikében éri el a bal szélső vonalat. A geometriai viszonyokból adódik, hogy
\(\displaystyle (k-1)d< 2L\tg\beta<2L\cdot \tg48{,}6^\circ=272{,}2\ \rm cm,\)
vagyis
\(\displaystyle k< 6{,}4.\)
Figyelembe véve, hogy \(\displaystyle k\) páratlan, \(\displaystyle k_\text{max}=5,\) vagyis (a rövidebb oldalon történő egyetlen visszaverődéssel együtt) a fénysugár legfeljebb 6-szor verődhet vissza.
Statisztika:
28 dolgozat érkezett. 5 pontot kapott: Arnold Lőrinc, Beke Bálint, Bunford Luca, Chrobák Gergő, Fajszi Karsa, Fehérvári Donát, Fórizs Borbála, Halász Henrik, Hegedűs Máté Miklós, Molnár Kristóf, Seprődi Barnabás Bendegúz, Szatmári András Gábor, Tomesz László Gergő. 4 pontot kapott: Bálint Máté, Schmercz Blanka. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2022. októberi fizika feladatai
