A P. 5434. feladat (2022. október)

P. 5434. Az ábrán szereplő feszültségforrás elektromotoros ereje bekapcsolás után időben lineárisan növekszik fel a kezdeti 0 voltos értékről; \(\displaystyle U(t)=U_0\frac{t}{t_0}\). A \(\displaystyle K\) kapcsoló segítségével bármelyik pillanatban rákapcsolható a feszültségforrás az áramkörre. A feszültségforrás bekapcsolása után mennyi idővel kell zárni a kapcsolót, hogy ezután az ellenálláson átfolyó áram erőssége időben lineárison nőjön? Milyen ütemben nő ekkor az áramerősség?

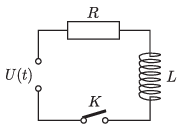
Közli: Széchenyi Gábor, Budapest

(5 pont)

A beküldési határidő 2022. november 15-én LEJÁRT.

Megoldás. Az áramerősség a kapcsoló zárásának \(\displaystyle T\) időpontjában nulla, hiszen a tekercs önindukciója miatt nem tud hirtelen megindulni az áram. Emiatt (ha az áramerősség időben lineárisan változik)

\(\displaystyle I(t)=\lambda(t-T) \qquad (t>T),\)

ahol \(\displaystyle \lambda\) (az egyik kérdezett mennyiség) az áramerősség növekedési üteme.

Az ohmos ellenállásra jutó feszültség

\(\displaystyle U_1=RI(t)=R\lambda (t-T),\)

a tekercsben indukálódott feszültség pedig

\(\displaystyle U_2=L\frac{\Delta I(t)}{\Delta t}=L\lambda.\)

Fennáll, hogy

\(\displaystyle U(t)=U_1+U_2,\)

vagyis

\(\displaystyle U_0\frac{t}{t_0}=R\lambda (t-T)+L\lambda.\)

Ennek az összefüggésnek minden időpillanatban fenn kell állnia, például \(\displaystyle t=0\) pillanatban

\(\displaystyle L\lambda-R\lambda T=0,\qquad \text{vagyis}\qquad T=\frac{L}{R},\)

továbbá \(\displaystyle t\) együtthatója az összefüggés bal és jobb oldalán ugyanakkora kell legyen, azaz

\(\displaystyle \frac{U_0}{t_0}=R\lambda, \qquad \text{tehát}\qquad \lambda=\frac{U_0}{Rt_0}.\)

Statisztika:

10 dolgozat érkezett.
5 pontot kapott:	Arnold Lőrinc, Bencz Benedek, Halász Henrik, Kollmann Áron Alfréd, Nemeskéri Dániel, Papp Marcell Imre, Tóth Kolos Barnabás, Vágó Botond.
4 pontot kapott:	Klement Tamás, Vincze Farkas Csongor.

A KöMaL 2022. októberi fizika feladatai