 |
A P. 5492. feladat (2023. május) |
P. 5492. Két egyforma, egyenként \(\displaystyle m\) tömegű testet egy elhanyagolható tömegű állócsigán átvetett rugalmas gumiszál köt össze. A testeket az ábrán látható helyzetben tartjuk – ekkor a gumiszál éppen nyújtatlan –, majd a \(\displaystyle B\) testet kezdősebesség nélkül elengedjük. Az \(\displaystyle A\) test az indítás után \(\displaystyle t_0\) idővel válik el az asztaltól.
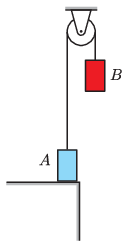
\(\displaystyle a)\) Mekkora a \(\displaystyle B\) test elmozdulása a \(\displaystyle t=t_0\) időpillanatban?
\(\displaystyle b)\) Az indítástól számítva mennyi idő múlva lesz a \(\displaystyle B\) test sebessége először nulla?
\(\displaystyle c)\) Mekkora a gumiszálat feszítő legnagyobb erő a mozgás során?
Közli: Vigh Máté, Biatorbágy
(5 pont)
A beküldési határidő 2023. június 15-én LEJÁRT.
I. megoldás. Feltételezzük, hogy a gumiszál követi a Hooke-törvényt, vagyis a benne ébredő \(\displaystyle F\) erő arányos az \(\displaystyle x\) megnyúlással. Az arányossági tényezőt (a gumiszál ,,rugóállandóját'') jelöljük a szokásos módon \(\displaystyle D\)-vel.
\(\displaystyle a)\) A rendszer mozgása két szakaszra bontható. Az I. szakaszban az \(\displaystyle A\) test mozdulatlan, a \(\displaystyle B\) test pedig \(\displaystyle t_0\) ideig harmonikus rezgőmozgást végez. Ez a szakasz addig tart, amíg a gumiszálban ébredő erő kisebb, mint \(\displaystyle mg\), vagyis a \(\displaystyle B\) test elmozdulása
| \(\displaystyle (1)\) | \(\displaystyle x<\frac{mg}{D}=x_0.\) |
A \(\displaystyle B\) test sebessége kezdetben nulla, \(\displaystyle t_0\) idő elteltével pedig a gyorsulása válik nullává, mert ekkor a gumiszál által kifejtett erő éppen az \(\displaystyle mg\) nehézségi erő \(\displaystyle (-1)\)-szerese, tehát a testre ható eredő erő nulla (1. ábra).

1. ábra
A harmonikus rezgőmozgás során a nulla sebességű és a nulla gyorsulású állapot között egy negyed periódusnyi idő telik el, vagyis
\(\displaystyle t_0=\frac{T}{4}=\frac{\pi}{2\omega}=\frac{\pi}{2}\sqrt{\frac{m}{D}},\)
és így
| \(\displaystyle (2)\) | \(\displaystyle \omega=\frac{\pi}{2t_0}\) |
Ezt (1)-gyel összevetve látjuk, hogy
| \(\displaystyle (3)\) | \(\displaystyle x_0=\frac{g}{\omega^2}=\frac4{\pi^2}gt_0^2,\) |
ekkora a \(\displaystyle B\) test elmozdulása a \(\displaystyle t_0\) idejű mozgás után.
A továbbiak szempontjából lényeges, hogy a \(\displaystyle B\) test sebessége a \(\displaystyle t_0\) idejű mozgás után
| \(\displaystyle (4)\) | \(\displaystyle v_0=x_0\omega=\frac{2}{\pi}gt_0.\) |
\(\displaystyle b)\) A mozgás második szakaszában mindkét test mozog. Tekintsük azt a helyzetet, amikor a \(\displaystyle B\) test elmozdulása \(\displaystyle x_0+x\), az \(\displaystyle A\) test az asztal fölött \(\displaystyle y\) magasságban van és az indulástól számítva \(\displaystyle t_0+t\), vagyis az \(\displaystyle A\) test megemelkedésének pillanatától mérve \(\displaystyle t\) idő telt el. A gumiszál megnyúlása ekkor \(\displaystyle x_0+x-y\), a szálat feszítő erő tehát
\(\displaystyle F=D(x_0+x-y).\)
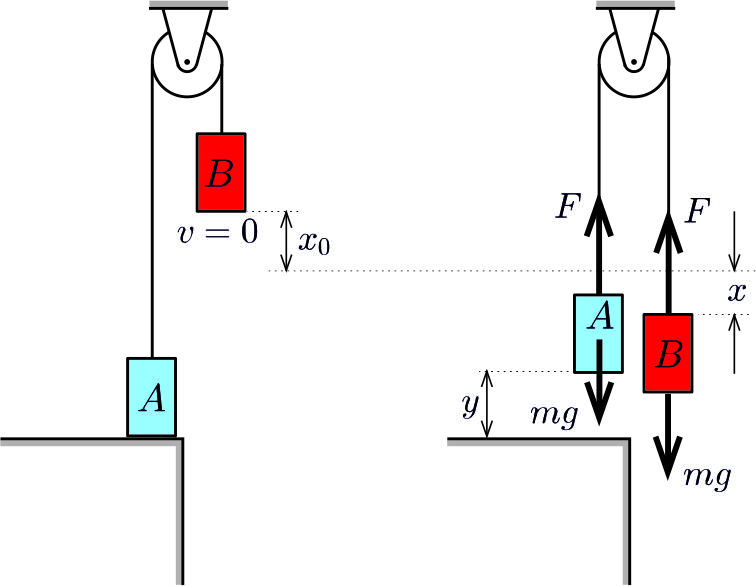
2. ábra
A testek mozgásegyenlete:
\(\displaystyle ma_x=mg-F=D(y-x), \qquad \text{illetve}\qquad ma_y=F-mg=D(x-y),\)
amiket így is felírhatunk:
| \(\displaystyle (5)\) | \(\displaystyle a_x=\omega^2(y-x)\) |
és
| \(\displaystyle (6)\) | \(\displaystyle a_y=\omega^2(x-y),\) |
és a kezdeti feltételek \(\displaystyle t=0\) pillanatban:
| \(\displaystyle (7)\) | \(\displaystyle x(0)=y(0)=0,\qquad v_x(0)=v_0, \qquad v_y(0)=0.\) |
(5) és (6) összegéből látszik, hogy az \(\displaystyle x(t)+y(t)\) mennyiség gyorsulása nulla, vagyis
| \(\displaystyle (8)\) | \(\displaystyle x(t)+y(t)=v_0\cdot t.\) |
Ez összhangban van a (7)-ben szereplő kezdeti feltételekkel.
(5) és (6) különbségét képezve:
\(\displaystyle a_{(x-y)}=-2\omega^2 (x-y),\)
ami egy \(\displaystyle \sqrt2\,\omega\) körfrekvenciájú harmonikus rezgőmozgás egyenlete. A kezdeti feltételeknek is eleget tevő megoldás:
| \(\displaystyle (9) \) | \(\displaystyle x(t)-y(t)=\frac{v_0}{\sqrt2\,\omega}\sin\left(\sqrt2\,\omega t\right).\) |
A \(\displaystyle B\) test mozgását leíró függvény (8) és (9) összegéből:
\(\displaystyle x(t)=\frac{v_0}{2}\left(t+\frac1{\sqrt2\,\omega}\sin (\sqrt2\,\omega t) \right),\)
és ennek megfelelően a \(\displaystyle B\) test sebessége:
\(\displaystyle v_x(t)=\frac{v_0}{2}\left(1+ \cos (\sqrt2\,\omega t) \right).\)
Ez a sebesség akkor válik nullává, amikor \(\displaystyle \sqrt2\,\omega t =\pi,\) vagyis
\(\displaystyle t=t_1=\frac{\pi}{\sqrt2\,\omega}=\sqrt2\,t_0.\)
Ennek megfelelően a \(\displaystyle B\) test sebessége az indulásától számítva
\(\displaystyle t_0+t_1=\left(1+\sqrt2\right)t_0\approx 2{,}41\,t_0\)
idő elteltével válik ismét nullává.
\(\displaystyle c)\) A gumiszálat feszítő erő akkor a legnagyobb, amikor az
\(\displaystyle x(t)-y(t)=\frac{v_0}{\sqrt2\,\omega}\sin\left(\sqrt2\,\omega t\right)\)
függvény maximális, nevezetesen
\(\displaystyle (x-y)_\text{max}=\frac{v_0}{\sqrt2\,\omega}=\frac1{\sqrt2}x_0\)
nagyságú. A gumiszálat feszítő erő ekkor
\(\displaystyle F_\text{max}=D\left(x_0+\frac1{\sqrt2}x_0\right)=\left(1+\frac1{\sqrt2}\right)mg\approx 1{,}71\ mg.\)
II. megoldás. Az állócsiga, mivel a tömege elhanyagolható, a gumiszálban ható erőnek csak az irányát változtatja meg, a nagyságát nem. Emiatt megtehetjük, hogy a gumiszálat (gondolatban) kiegyenesítjük, és a két test mozgását egy vízszintes, súrlódásmentes lapon vizsgáljuk. Az állócsigán lógó testekre ható nehézségi erőt ebben a ,,kiegyenesített'' elrendezésben egy-egy vízszintesen, \(\displaystyle mg\) nagyságú, ellentétes irányú külső erővel vehetjük figyelembe. Az eredeti asztal szerepét egy függőleges támaszték veszi át, amely egy ideig (amíg a gumiszálat feszítő erő kisebb, mint \(\displaystyle mg\)) megakadályozza az \(\displaystyle A\) test elmozdulását (3. ábra).

3. ábra
\(\displaystyle a)\) A mozgás kezdeti szakaszában az \(\displaystyle A\) test mozdulatlan, gyorsulása nulla. A gumiszálban ébredő \(\displaystyle F\) erő és az \(\displaystyle mg\) külső erő különbségét a függőleges támaszték által kifejtett \(\displaystyle K=mg-F\) nagyságú nyomóerő ,,egyensúlyozza ki''. Mivel \(\displaystyle K\ge0,\) ez a helyzet csak addig állhat fenn, amíg \(\displaystyle B\) test elmozdulása nem lépi túl a kritikus
\(\displaystyle x_0=\frac{mg}{D}\)
értéket. (Itt és a továbbiakban az I. megoldás jelöléseit használjuk.)
A \(\displaystyle B\) test eközben az elmozdulásával arányosan csökkenő gyorsulással, tehát \(\displaystyle \omega=\sqrt{D/m}\) körfrekvenciájú harmonikus rezgőmozgásnak megfelelő mozgást végez. A rezgőmozgás ,,egyensúlyi helyzete'' éppen az \(\displaystyle x_0\) elmozdulásnál lesz, itt válik a \(\displaystyle B\) test gyorsulása nullává. Kezdetben a \(\displaystyle B\) test sebessége nulla, tehát \(\displaystyle x_0\) elmozdulásáig éppen egy negyed periódus telik.
\(\displaystyle t_0=\frac14T=\frac14\cdot \frac{2\pi}{\omega},\)
vagyis
| \(\displaystyle (10)\) | \(\displaystyle \omega=\frac{\pi}{2t_0},\) |
és így
| \(\displaystyle (11)\) | \(\displaystyle x_0=\frac{mg}{D}=\frac{g}{\omega^2}=\frac{4gt_0^2}{\pi^2}.\) |
Az \(\displaystyle A\) test megmozdulásának pillanatában (4. ábra) a \(\displaystyle B\) test valamekkora \(\displaystyle v_0\) sebességgel rendelkezik. Ennek nagyságát a munkatétel alkalmazásával határozhatjuk meg:
\(\displaystyle mgx_0=\frac12Dx_0^2+\frac12mv_0^2,\)
ahonnan (10) és (11) felhasználásával:
| \(\displaystyle (12)\) | \(\displaystyle v_0=\sqrt{2gx_0-\omega^2x_0^2}=\frac{g}{\omega}=\frac2{\pi}gt_0.\) |
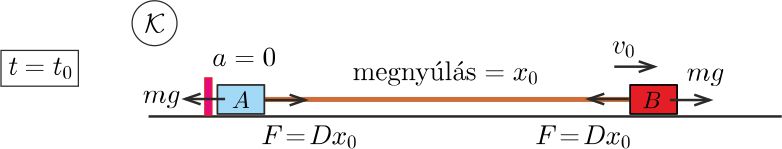
4. ábra
\(\displaystyle b)\) A mozgás további részében a külső erők (\(\displaystyle mg\) és \(\displaystyle -mg\)) eredője nulla, tehát a két testből álló rendszer lendülete időben állandó, a kezdeti \(\displaystyle mv_0\)-lal egyezik meg.
Térjünk át az asztal \(\displaystyle \cal K\) koordináta-rendszeréről a tömegközépponti, \(\displaystyle \cal K\)-hoz képest \(\displaystyle v_0/2\) sebességgel mozgó \(\displaystyle \cal K'\) vonatkoztatási rendszerre. Ebben a rendszerben a gumiszál \(\displaystyle S\) középpontja áll, az rögzítettnek is tekinthető.
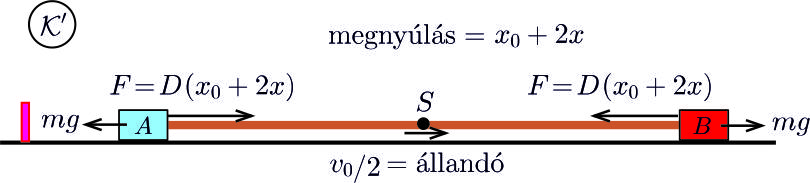
5. ábra
A fél gumiszál rugóállandója \(\displaystyle 2D\), hiszen adott feszítőerő hatására a gumi fele csak feleannyit nyúlik meg, mint a gumiszál egésze. A testek kezdősebessége a tömegközépponti rendszereben:
\(\displaystyle v'_A=0-\frac{v_0}{2}=-\frac{v_0}{2}, \qquad \text{illetve}\qquad v'_B=v_0-\frac{v_0}{2}=+\frac{v_0}{2}.\)
Amikor a fél gumiszál hossza \(\displaystyle \frac12x_0+x\), akkor a \(\displaystyle B\) testre ható erő:
\(\displaystyle F(x)=-2D\left(\frac12x_0+x\right)+mg=-2Dx,\)
a \(\displaystyle B\) test tehát
\(\displaystyle \omega'=\sqrt{\frac{2D}{m}}=\sqrt2\,\omega\)
körfrekvenciájú rezgésbe kezd.
Amikor a \(\displaystyle B\) test sebessége a \(\displaystyle \cal K\) rendszerben nulla, akkor a tömegközépponti \(\displaystyle \cal K'\) rendszerben a sebessége \(\displaystyle -v_0/2\), vagyis a kezdeti érték \(\displaystyle (-1)\)-szerese. Ezt a sebességet az \(\displaystyle A\) test megindulásától számítva éppen egy fél periódusnyi idő alatt éri el, ami
\(\displaystyle t_1=\frac{T'}{2}=\frac{\pi}{\omega'}=\frac{\pi}{\sqrt2\omega }=\sqrt2\,t_0.\)
A \(\displaystyle B\) test elindulásától számítva az első megállásáig tehát
\(\displaystyle t_0+t_1=\left(1+\sqrt{2}\right)t_0\)
idő telik el.
\(\displaystyle c)\) A gumiszálat feszítő erőt a gumiszál legnagyobb megnyúlása határozza meg. Ez legkönnyebben a \(\displaystyle \cal K'\) rendszerben kaphatjuk meg. Ha az egyes testek rezgési amplitúdója \(\displaystyle A\), akkor a legnagyobb megnyúlás \(\displaystyle x_0+2A\), és így
\(\displaystyle F_\text{max}=D\left(x_0+2A\right).\)
Az \(\displaystyle A\) amplitúdót a munkatételből határozhatjuk meg:
\(\displaystyle \cfrac{m}{2}\left(\frac{v_0}{2}\right)^2=\frac12(2D)A^2,\)
ahonnan
\(\displaystyle A=\sqrt{\cfrac{m}{8D}}v_0=\frac{1}{\sqrt8}x_0,\)
vagyis
\(\displaystyle F_\text{max}=\left(1+\frac{1}{\sqrt{2}} \right) mg.\)
Statisztika:
13 dolgozat érkezett. 5 pontot kapott: Halász Henrik, Kis Márton Tamás. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2023. májusi fizika feladatai
