 |
A P. 5494. feladat (2023. május) |
P. 5494. Az ábrán látható ,,kettős jojó'' két egyforma, homogén tömegeloszlású korongból és a rájuk tekert fonalakból áll.
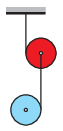
A két testet a fonalak függőleges helyzetéből kezdősebesség nélkül indítjuk el. Mennyi idő alatt tekeredik le az alsó korongról a rajta lévő 80 cm hosszúságú fonál?
Példatári feladat nyomán
(5 pont)
A beküldési határidő 2023. június 15-én LEJÁRT.
Megoldás. Legyen a korongok tömege \(\displaystyle m\), sugaruk \(\displaystyle R\), és így a tehetetlenségi nyomatékuk \(\displaystyle \tfrac12mR^2\). Jelöljük a felső korong tömegközéppontjának gyorsulását \(\displaystyle a_1\)-gyel, az alsó korongét \(\displaystyle a_2\)-vel, a felső fonalat feszítő erőt \(\displaystyle F_1\)-gyel, az alsó fonalét pedig \(\displaystyle F_2\)-vel (lásd az ábrát).
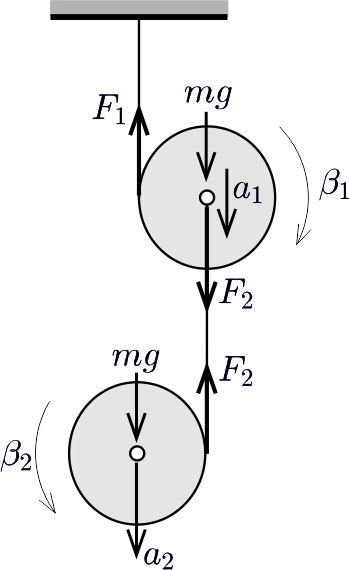
A korongok szöggyorsulása (a fonalak nyújthatatlansága miatt)
| \(\displaystyle (1)\) | \(\displaystyle \beta_1=\frac{a_1}{R}\) |
és
| \(\displaystyle (2)\) | \(\displaystyle \beta_2=\frac{a_2-a_1}{R}.\) |
A korongok tömegközéppontjainak mozgásegyenlete:
| \(\displaystyle (3)\) | \(\displaystyle mg+F_2-F_1=ma_1,\) |
| \(\displaystyle (4)\) | \(\displaystyle mg-F_2=ma_2,\) |
a forgómozgások egyenletei pedig
| \(\displaystyle (5) \) | \(\displaystyle F_1R=\frac12mR^2\,\beta_1\) |
és
| \(\displaystyle (6) \) | \(\displaystyle F_2R=\frac12mR^2\,\beta_2.\) |
Az (1)-(6) lineáris egyenletrendszer megoldása:
\(\displaystyle a_1=\cfrac{8}{11}\,g, \qquad a_2=\cfrac{10}{11}\,g,\)
\(\displaystyle F_1= \cfrac{4}{11}\,mg, \qquad F_2= \cfrac{1}{11}\,mg.\)
\(\displaystyle \beta_1=\cfrac{8}{11}\cfrac{g}{R}\qquad \text{és}\qquad \beta_2=\cfrac{2}{11}\cfrac{g}{R}.\)
Ha az alsó korongról az \(\displaystyle s=0{,}8\ \)m hosszúságú fonál \(\displaystyle t\) idő alatt tekeredik le, akkor fennáll:
\(\displaystyle s=\frac{R\beta_2}{2}t^2,\)
ahonnan
\(\displaystyle t=\sqrt{\frac{11s}{g}}=0{,}95\ \rm s.\)
Statisztika:
13 dolgozat érkezett. 5 pontot kapott: Csiszár András, Fehérvári Donát, Kis Márton Tamás, Tárnok Ede , Vágó Botond. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2023. májusi fizika feladatai
