A P. 5496. feladat (2023. május)

P. 5496. Az ábrán látható módon egy 10 cm átmérőjű, tükrözödő felületű hengert egy 5 mm átmerőjű lézersugárral világítunk meg. A visszaverődő lézersugárra merőlegesen egy ernyőt helyezünk el úgy, hogy a visszaverődési pont és az ernyő között a távolság 20 cm. Milyen alakú és méretű fényfolt keletkezik az ernyőn?

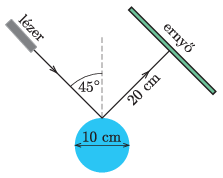
Közli: Széchenyi Gábor, Budapest

(5 pont)

A beküldési határidő 2023. június 15-én LEJÁRT.

Megoldás. Jelöljük a lézerfénynyaláb átmérőjét \(\displaystyle d\)-vel, a henger sugarát \(\displaystyle R\)-rel, továbbá a fénysugár tükröződési pontja és az ernyő közötti távolságot \(\displaystyle D\)-vel. (A feladat szövege szerint \(\displaystyle d=0{,}5\ \rm cm\), \(\displaystyle R=5\ \rm cm\) és \(\displaystyle D=20\ \rm cm\).) A továbbiakban kihasználjuk, hogy \(\displaystyle \frac{d}{R}=\frac{1}{10}\ll 1.\)

1. ábra

A lézernyaláb tengelyében haladó fénysugár a \(\displaystyle C\) pontban éri el a henger felületét (1. ábra). Vizsgáljuk meg, merre verődik vissza az a fénysugár, amelyik az ábra síkjában halad, és a középső fénysugártól mért (előjeles) távolsága \(\displaystyle x\). (Nyilván \(\displaystyle \vert x\vert\le d/2\).) Ez a fénysugár a hengerfelületet olyan \(\displaystyle P\) pontban éri el, amelyre \(\displaystyle PC\approx\sqrt2\,x\). (Kihasználtuk, hogy \(\displaystyle \vert x\vert\ll R\), és emiatt a \(\displaystyle PQC\triangle\) jó közelítéssel egyenlő szárú derékszögű háromszög. Mivel a \(\displaystyle P\) pontbeli érintősík a \(\displaystyle C\) ponthoz tartozó érintősíkkal

\(\displaystyle POC\angle\equiv \varphi\approx \frac{\sqrt2\,x}{R}\)

szöget zár be, a \(\displaystyle P\) pontból és a \(\displaystyle C\) pontból visszaverődő fénysugarak egymással bezárt szöge \(\displaystyle 2\varphi.\) Ennek a két fénysugárnak a kezdeti távolsága \(\displaystyle x\), de mire elérik a \(\displaystyle D\) távol lévő ernyőt, a távolságuk

\(\displaystyle C'P'\approx x+2D\,\varphi= \left(1+2D\frac{\sqrt2 }{R}\right)x\equiv \lambda\cdot x\)

lesz. (Itt ismét kihasználtuk, hogy \(\displaystyle \varphi\ll 1\).)

Látható, hogy az ernyőhöz érkező lézerfénynyaláb az ábra síkjában az eredeti méretének \(\displaystyle \lambda\)-szorosára szélesedik, tehát a teljes szélessége

\(\displaystyle 2\left(C'P'\right)_\text{max}=\left(1+2D\frac{\sqrt2 }{R}\right)d\approx 6{,}7\ \rm cm\)

lesz.

A fénynyaláb a henger tengelyének irányban egyáltalán nem szélesedik ki, hiszen az ugyanakkora \(\displaystyle x\) értékhez tartozó, de egymás ,,mögött'' haladó fénysugarak beesési szöge ugyanakkora, tehát a visszaverődési szögük sem tér el egymástól. Ezen sugarak távolsága az ernyőn az eredeti \(\displaystyle d=0{,}5\ \rm cm\) nagyságú marad.

Összefoglalva: az ernyőre érkező fénynyaláb szélessége az egyik irányban jelentősen megnyúlik, a másik (az előbbire merőleges) irányban változatlan marad, tehát az ernyőn a fényfolt (jó közelítéssel) egy \(\displaystyle a=6{,}1\ \rm cm\) nagytengelyű, \(\displaystyle b=0{,}5\ \rm cm\) kistengelyű ellipszis lesz (2. ábra).

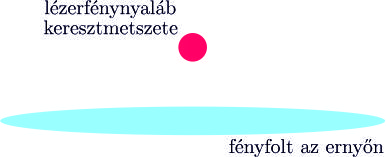
2. ábra

Statisztika:

5 dolgozat érkezett.
5 pontot kapott:	Tomesz László Gergő, Waldhauser Miklós.
4 pontot kapott:	Fajszi Karsa, Tárnok Ede .

A KöMaL 2023. májusi fizika feladatai