 |
A P. 5563. feladat (2024. április) |
P. 5563. Az \(\displaystyle M\) és \(\displaystyle m\) tömegű, kis méretű testeket \(\displaystyle \ell\) hosszúságú fonállal kötjük össze. A \(\displaystyle M\) tömegű testhez egy másik fonalat is erősítünk, és annak felső végét kicsiny amplitúdóval, \(\displaystyle T\) periódusidejű harmonikus rezgőmozgással vízszintesen mozgatjuk. Mekkora \(\displaystyle \ell\) hossz esetén maradhat a rezgetett fonál mindvégig függőleges?
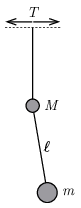
Kvant
(5 pont)
A beküldési határidő 2024. május 15-én LEJÁRT.
Megoldás. Az \(\displaystyle M\) és \(\displaystyle m\) tömegű testekből álló rendszerre ható külső erőknek (a függőleges fonál által kifejtett erőnek és a nehézségi erőknek) nincs vízszintes összetevője, emiatt a rendszer tömegközéppontja, amely az alsó testtől \(\displaystyle \ell'=\frac{M}{M+m}\ell\) távolságra van, vízszintes irányba nem mozdul el. (A tömegközéppont függőleges elmozdulása ugyancsak nullának tekinthető, hiszen a lengés amplitúdója kicsi, a függőleges elmozdulás pedig másodrendűen kicsi.) A tömegközéppontnál a fonalat akár rögzíthetjük is, hiszen úgysem mozdul el. Így egy \(\displaystyle \ell'\) hosszúságú matematikai ingát kapunk, amelynek lengésideje
\(\displaystyle T=2\pi\sqrt{\frac{\ell'}{g}}=2\pi\sqrt{\frac{\ell M}{(M+m)g}}.\)
Ezek szerint
\(\displaystyle \ell=g\left(1+\frac{m}{M}\right)\left(\frac{T}{2\pi}\right)^2.\)
Statisztika:
15 dolgozat érkezett. 5 pontot kapott: Csapó András, Csiszár András, Czirják Márton Pál, Dobos Anita, Hegedüs Márk, Seprődi Barnabás Bendegúz, Szabó Donát, Tóth Kolos Barnabás. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző.
A KöMaL 2024. áprilisi fizika feladatai
