 |
A P. 5566. feladat (2024. április) |
P. 5566. Vízszintes, nem teljesen sima asztallapon egymást majdnem érintve nyugszik egy \(\displaystyle 2r\) és egy \(\displaystyle r\) sugarú korong. A síkon egy harmadik, \(\displaystyle 3r\) sugarú korong forgásmentesen csúszik úgy, hogy a sebességvektora a három korong közös érintőjével párhuzamos (lásd a felülnézeti ábrát). Mindhárom korong ugyanabból az anyagból készült és a magasságuk is ugyanakkora.
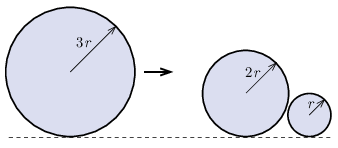
A rugalmasnak tekinthető ütközés után a \(\displaystyle 3r\) sugarú korong a súrlódás miatt lelassul és \(\displaystyle d=5~\mathrm{cm}\) út megtétele után megáll. Milyen irányban és milyen messzire jutnak el a kisebb korongok az asztalon? A korongok közötti súrlódás elhanyagolható.
Útmutatás: Lásd a P. 5555. feladatot lapunk 2024. márciusi számában és a Komplex számok a fizikában I. cikket a jelen számban.
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2024. május 15-én LEJÁRT.
I. megoldás. Az ütközés nagyon rövid ideje alatt a külső erők (az asztallap és a korongok közötti súrlódás) hatása figyelmen kívül hagyható, vagyis a három korongból álló rendszer zártnak tekinthető. Az ütközések során a teljes mozgásmennyiség (impulzus) vektora állandó marad. Az ütközés rugalmas, így az ütköző korongok összes mozgási energiája sem változik meg. A korongok közötti súrlódás elhanyagolható, emiatt a korongok nem jöhetnek forgásba, vagyis a mozgási energia tisztán a transzlációs mozgásból származik.
A korongok tömege az alapterületükkel, vagyis a sugaruk négyzetével arányos: \(\displaystyle 9m\), \(\displaystyle 4m\), \(\displaystyle m\).
Vizsgáljuk először a \(\displaystyle 9m\) és a \(\displaystyle 4m\) tömegű korong ütközését. Jelöljük a nagyobb korong ütközés előtti sebességvektorát \(\displaystyle \boldsymbol{v}_0\)-lal. Az ütközés pillanatában (lásd az 1. ábrát) a korongok \(\displaystyle P\) és \(\displaystyle Q\) középpontjára illeszkedő egyenesnek a nagyobb korong kezdeti mozgásirányával bezárt szöge:
| \(\displaystyle (1)\) | \(\displaystyle \varphi=\arcsin\frac{1}{5}=11{,}54^\circ.\) |
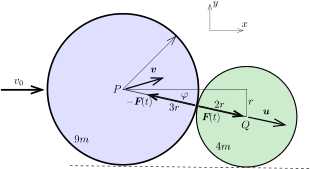
1. ábra
Az ütközés során a két korong között egy nagyon rövid ideig tartó, nagyon nagy \(\displaystyle \boldsymbol{F}(t)\) erő lép fel, ami a kezdetben álló kisebb korongot \(\displaystyle \overrightarrow{PQ}\) irányba valamekkora \(\displaystyle \boldsymbol{u}\) sebességgel meglöki. Eközben a nagyobb korong sebessége \(\displaystyle \boldsymbol{v}\)-re változik. A kisebb korong az ütközés előtt állt, így \(\displaystyle \boldsymbol{u}\) iránya nyilván megegyezik \(\displaystyle \boldsymbol{F}\) irányával.
Az ábrán látható koordináta-rendszerben az impulzusmegmaradás törvénye szerint
\(\displaystyle (9m)v_0=(9m)v_x+(4m)u\cos\varphi,\)
\(\displaystyle 0=(9m)v_y-(4m)u\sin\varphi,\)
vagyis
| \(\displaystyle (2)\) | \(\displaystyle v_x=v_0-\frac{4}{9}{u\cos\varphi},\) |
| \(\displaystyle (3)\) | \(\displaystyle v_y= \frac{4}{9}{u\sin\varphi}.\) |
Az energiamegmaradás törvényét alkalmazva felírhatjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \frac{1}{2}(9m)v_0^2=\frac{1}{2}(9m)\left(v_x^2+v_y^2\right)+\frac{1}{2}(4m)u^2.\) |
(2)-t és (3)-t (4)-be helyettesítve az \(\displaystyle u\) sebességnagyságra egy hiányos másodfokú egyenletet kapunk, aminek az egyik (számunkra érdektelen) megoldása \(\displaystyle u=0\), a másik gyöke pedig
| \(\displaystyle (5)\) | \(\displaystyle u=\frac{18}{13}v_0\cos\varphi=\frac{18\sqrt{24}}{65}v_0\approx 1{,}36\,v_0.\) |
(2), (3) és (5) felhasználásával a korongok sebességkomponensei:
\(\displaystyle u_x=u\cos\varphi=1{,}33\,v_0,\)
\(\displaystyle u_y=-u\sin\varphi=-0{,}27\,v_0,\)
\(\displaystyle v_x=0{,}41\,v_0,\)
\(\displaystyle v_y=0{,}12\,v_0.\)
A \(\displaystyle 4m\) tömegű korong ezután ütközik az \(\displaystyle m\) tömegű álló koronggal, és a sebességük az ütközés után \(\displaystyle \boldsymbol{w}\)-re és \(\displaystyle \boldsymbol{z}\)-re változik (2. ábra). Az ütközés ferdeségére jellemző szög a második ütközésnél
\(\displaystyle \psi=\arcsin\frac{1}{3}\approx 19{,}47^\circ.\)
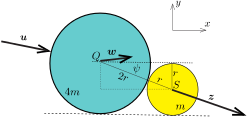
2. ábra
A legkisebb korong ütközés utáni sebessége az erőlökéssel párhuzamos, vagyis \(\displaystyle \overrightarrow{QS}\) irányú, derékszögű komponensei tehát \(\displaystyle z_x=z\cos\psi\) és \(\displaystyle z_y=-z\sin\psi\).
Erre az ütközésre is felírhatjuk a megmaradási törvényeket:
| \(\displaystyle (6)\) | \(\displaystyle (4m)u_x=(4m)w_x+m\,z_x,\) |
| \(\displaystyle (7)\) | \(\displaystyle (4m)u_y=(4m)w_y+m\,z_y,\) |
| \(\displaystyle (8)\) | \(\displaystyle \frac{1}{2}(4m)\left(u_x^2+u_y^2\right)=\frac{1}{2}(4m)\left(w_x^2+w_y^2\right)+\frac{1}{2}m\,z^2.\) |
(6) és (7)-ből kifejezve \(\displaystyle w_x\) és \(\displaystyle w_y\)-t, és ezeket (8)-ba helyettesítve \(\displaystyle z\)-re hiányos másodfokú egyenletet kapunk, aminek nullától különböző megoldása:
\(\displaystyle z=\frac{8}{5}\left(u_x\cos\psi-u_y\sin\psi\right)\approx 2{,}15\,v_0.\)
Ennek megfelelően a középső korong sebessége a második ütközés után
\(\displaystyle \boldsymbol{w}=(0{,}82;\,-0{,}09)\,v_0,\)
a legkisebb korongé
\(\displaystyle \boldsymbol{z}=(2{,}03;\,-0{,}72)\,v_0.\)
A legnagyobb korong végsebessége, mint azt korábban láttuk
\(\displaystyle \boldsymbol{v}=(0{,}41; \, 0{,}12)\,v_0.\)
Megjegyzés. Elképzelhető lenne, hogy a középső korong a második ütközés után még egyszer ütközik a legnagyobb méretű koronggal. Ez azonban a jelen esetben nem következik be, hiszen a \(\displaystyle \boldsymbol{w}-\boldsymbol{v}\) relatív sebességvektor és a korongok középpontját összekötő \(\displaystyle \overrightarrow{PQ}=(\sqrt{24};-1)\) vektor skalárszorzata pozitív, vagyis ezen két korong középpontjai a második ütközés után távolodnak egymástól.
A legnagyobb korong az eredeti mozgásirányához képes
\(\displaystyle \alpha_3=\arctg\frac{v_y}{v_x}=16{,}3^\circ\)
szögben ,,balra'' (az óramutató járásával ellentétesen) térül el, a középső korong elmozdulásának iránya
\(\displaystyle \alpha_2=\arctg\frac{\vert w_y\vert}{w_x}=6{,}3^\circ,\)
míg a legkisebb korong
\(\displaystyle \alpha_2=\arctg\frac{\vert z_y\vert}{z_x}=-19{,}5^\circ\)
szögben ,,jobbra'' (az óramutató járásával megegyező irányba) térül el.
Az asztallapon csúszó korongok az asztallal való súrlódásuk miatt ugyanolyan ütemben (\(\displaystyle a=-\mu g\) ,,gyorsulással'') egyenletesen lassulva mozognak, a megállásukig megtett útjuk a kezdősebességük négyzetével arányos. Mivel
\(\displaystyle v^2:w^2:z^2=0{,}18:0{,}68:4{,}62\approx 5\,\mathrm{cm}:19\,\mathrm{cm}:128\,\mathrm{cm},\)
ha a legnagyobb korong \(\displaystyle d=5\,\mathrm{cm}\) út megtétele után áll meg, akkor a középső kb. \(\displaystyle 19\,\mathrm{cm}\)-re jut el, a legkisebb pedig majdnem \(\displaystyle 1{,}3\,\mathrm{m}\) utat tesz meg a megállásáig.
II. megoldás. A feladat a hivatkozott cikk összefüggései segítségével is megoldható. Az I. megoldás jelöléseit követjük, és a síkbeli vektoroknak komplex számokat feleltetünk meg. Így pl. \(\displaystyle \boldsymbol{v}=(v_x,v_y)\) komplex megfelelője a \(\displaystyle v=v_x+iv_y,\) és hasonlóan a többi vektornál is. (Figyelem: Az I. megoldásban \(\displaystyle v\) a \(\displaystyle \boldsymbol{v}\) vektor nagyságát jelölte, itt viszont a teljes \(\displaystyle \boldsymbol{v}\) vektornak megfeleltetett komplex számmal egyezik meg.)
Ha egy nagyobb korong \(\displaystyle \boldsymbol{v}_0\) sebességgel nekiütközik a nála \(\displaystyle k\)-szor kisebb tömegű álló korongnak, akkor az idézett cikk képleteinek megfelelően az ütközés után a nagyobb korong sebessége
\(\displaystyle v=\frac{kv_0+\mathrm{e}^{2i\alpha}\,\overline{v_0}}{k+1},\)
a kisebb korongé pedig
\(\displaystyle u=\frac{k}{k+1}(v_0-\mathrm{e}^{2i\alpha}\,\overline{v_0}).\)
A fenti képletekben \(\displaystyle \alpha\) a korongok közös érintőjének a Gauss-számsík valós tengelyével bezárt szöge.
Az első ütközésnél \(\displaystyle k=\frac{9}{4}=2{,}25\), valamint
\(\displaystyle \alpha=\frac{\pi}{2}-\varphi=\arccos\frac{1}{5}=78{,}46^\circ=1{,}369\,\mathrm{rad},\)
és ennek megfelelően
\(\displaystyle \mathrm{e}^{2i\alpha}=-0{,}921+0{,}392\,i.\)
(A továbbiakban ezt a komplex számot \(\displaystyle q\)-val fogjuk jelölni.)
Válasszuk a legnagyobb korong ütközés előtti sebességének \(\displaystyle \vert\boldsymbol{v}_0\vert\) nagyságát 1-nek. Ekkor a legnagyobb korong kezdeti sebessége \(\displaystyle v_0=1+0\cdot i=1\) valós szám, aminek a komplex konjugáltja is ugyanekkora.
Az ütközés utáni sebességek
\(\displaystyle v=\frac{2{,}25+q}{3{,}25}=0{,}409+0{,}121\,i,\qquad\textrm{valamint}\qquad u=\frac{2{,}25}{3{,}25}(1-q)=1{,}329-0{,}271\,i.\)
Megjegyzés. A komplex számok közötti algebrai műveleteket akár ,,kézzel'', egy zsebszámológéppel is elvégezhetjük, de a GeoGebra vagy a WolframAlpha program segítségével sokkal gyorsabban és kényelmesebben célhoz érhetünk.
A második ütközésnél a tömegarány \(\displaystyle k'=4\), valamint
\(\displaystyle \alpha'=\frac{\pi}{2}-\psi=\arccos\frac{1}{3},\)
és ennek megfelelően
\(\displaystyle q'=\mathrm{e}^{2i\alpha'}=-0{,}778+0{,}629\,i.\)
A középső (\(\displaystyle 2r\) sugarú) korong ütközés előtti sebességét az első ütközésnél kiszámított \(\displaystyle u\) komplex számmal adhatjuk meg.
A második ütközés utáni sebességek:
\(\displaystyle w=\frac{4u+q'\overline{u}}{5}=0{,}823-0{,}092\,i,\qquad\textrm{illetve}\qquad z=\frac{4}{5}(u-q\overline{u} )=2{,}027-0{,}717\,i.\)
A korongok ütközések utáni sebességnégyzeteinek aránya
\(\displaystyle v\overline{v}:w\overline{w}:z\overline{z}=0{,}18:0{,}68:4{,}62,\)
és ugyanilyen arányban állnak a megállásukig megtett utak is.
Statisztika:
19 dolgozat érkezett. 5 pontot kapott: Czirják Márton Pál, Dobos Anita, Fehérvári Donát, Szabó Donát. 4 pontot kapott: Bélteki Teó, Hornok Máté, Kiss 131 Adorján Timon. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2024. áprilisi fizika feladatai
