 |
A P. 5568. feladat (2024. április) |
P. 5568. Egymástól \(\displaystyle d\) távolságra lévő \(\displaystyle R\) sugarú (\(\displaystyle d>2R\)) kör alakú tartományban (két fekete kör) a homogén térben a mágneses indukció nagysága \(\displaystyle B\), és az ábra síkjára merőlegesen, azonos irányba mutat. A \(\displaystyle Q\) töltésű, \(\displaystyle m\) tömegű, pontszerű részecske \(\displaystyle v\) sebességgel az ábrán látható periodikus pályán mozog (piros görbe). Mennyi idő alatt tesz meg egy periódust a részecske? Mekkora lehet a mágneses indukció legkisebb értéke, hogy még kialakuljon periodikus pálya?
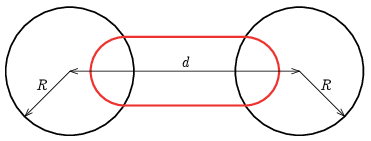
Közli: Cserti József, Budapest
(4 pont)
A beküldési határidő 2024. május 15-én LEJÁRT.
Megoldás. A mágneses térben a töltés a Lorentz-erő hatására \(\displaystyle \omega_\mathrm{c}=v/r_\mathrm{c}\) szögsebességgel \(\displaystyle r_\mathrm{c}\) sugarú körpályán mozog:
\(\displaystyle QB\omega_\mathrm{c}r_\mathrm{c}=m\omega_\mathrm{c}^2r_\mathrm{c},\)
amiből:
\(\displaystyle \omega_\mathrm{c}=\frac{QB}{m},\quad r_\mathrm{c}=\frac{v}{\omega_\mathrm{c}}=\frac{mv}{QB}.\)
Megjegyzés. A c index a ciklotronra utal lásd: https://hu.wikipedia.org/wiki/Ciklotron
A periódusidő két részből áll: egy teljes kör (két félkör) befutása a körpályán és a két egyenes szakasz megtétele:
$$\begin{align*} T &=t_1+t_2,\quad\textrm{ahol}\\ t_1 &=\frac{2\pi}{\omega_\mathrm{c}},\quad t_2=\frac{2\left(d-2\sqrt{R^2-r_\mathrm{c}^2}\right)}{v},\quad\textrm{amiből}\\ T &=\frac{2\pi m}{QB}+\frac{2d}{v}-4\sqrt{\left(\frac{R}{v}\right)^2-\left(\frac{m}{QB}\right)^2}. \end{align*}$$A geometria miatt \(\displaystyle r_\mathrm{c}\leq R\), vagyis a minimális mágneses indukció értéke:
\(\displaystyle B_\mathrm{min}=\frac{mv}{QR},\)
periodikus pálya csak \(\displaystyle B\geq B_\mathrm{min}\) esetén alakul ki.
Statisztika:
32 dolgozat érkezett. 4 pontot kapott: Bélteki Teó, Bencze Mátyás, Bogdán Benedek, Csapó András, Csernyik Péter, Csiszár András, Csóka Péter, Czirják Márton Pál, Debreceni Dániel, Erős Fanni, Fehérvári Donát, Fekete Lúcia, Gerendás Roland, Gyenes Károly, Klement Tamás, Kovács Kristóf , Magyar Zsófia, Masa Barnabás, Rózsa Laura Enikő , Szabó Donát, Tárnok Ede . 3 pontot kapott: Dobos Anita, Kiss 131 Adorján Timon. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2024. áprilisi fizika feladatai
