A P. 5571. feladat (2024. május)

P. 5571. Egy $\displaystyle h$ magasságú asztal sarka felett ugyancsak $\displaystyle h$ magasságból egy kicsiny golyót ejtünk el. Az asztal sarkától legfeljebb milyen távol érkezhet a golyó a talajra? Az ütközést tekintsük tökéletesen rugalmasnak.

Közli: Simon Péter, Pécs

(5 pont)

A beküldési határidő 2024. június 17-én LEJÁRT.

I. megoldás. A mozgás első szakaszában a golyó szabadeséssel megtesz $\displaystyle h$ utat, majd $\displaystyle v=\sqrt{2gh}$ sebességgel az asztal sarkához érkezik. Innen ugyanakkora sebességgel ismeretlen szögben elpattan (ferde hajítás), és szintén $\displaystyle h$ távolsággal mélyebben talajt ér. A ferde hajítások következő tulajdonságát fogjuk kihasználni: a $\displaystyle v$ sebességgel elhajított test $\displaystyle t$ idő múlva $\displaystyle vt$ távolságra lesz az ugyanakkor, ugyanonnan álló helyzetből induló, szabadeséssel gyorsuló képzeletbeli ponttól. Ez a pont $\displaystyle t$ időpontban a talajtól $\displaystyle h-\tfrac{1}{2}gt^2$ magasságban lesz. A két távolságból Pitagorasz tétellel kapjuk meg a hajítás $\displaystyle d$ vízszintes távolságát a $\displaystyle t$ ideig repülő golyóra:

$\displaystyle d^2=(vt)^2-\left(h-\frac{1}{2}gt^2\right)^2=-\frac{1}{4}g^2t^4+3hgt^2-h^2,$

ahol a második lépésben behelyettesítettük $\displaystyle v$ ismert értékét. A jobb oldali kifejezés az időnek negyedfokú, $\displaystyle t^2$-nek másodfokú polinomja, és csak egy bizonyos időtartományban pozitív – amikor talajt érhet a golyó. Hogy megtaláljuk az idő szerinti maximumát, alakítsuk teljes négyzetté:

$\displaystyle d^2=-\left(\frac{1}{2}gt^2-3h\right)^2+8h^2.$

Ezen már látszik, hogy akkor van maximuma, amikor a zárójelen belüli kifejezés zérus, azaz amikor $\displaystyle t=\sqrt{\tfrac{6h}{g}}$ ideig tart a ferde hajítás. A maximum értéke $\displaystyle d_\mathrm{max}^2=8h^2$, vagyis a vízszintes távolság maximuma

$\displaystyle d_\mathrm{max}=2\sqrt2h.$

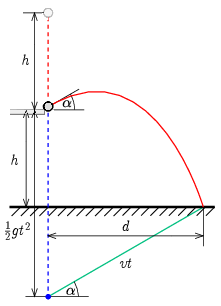
II. megoldás. A golyó az asztal sarkától a vízszintessel $\displaystyle \alpha$ szöget bezáró, $\displaystyle v=\sqrt{2gh}$ nagyságú sebességgel pattan el. A pályához tartozó vízszintes és függőleges elmozdulás:

$$\begin{align*} d&=\sqrt{2gh}\cos\alpha\,t\\ h&=\frac{1}{2}gt^2-\sqrt{2gh}\sin\alpha\,t, \end{align*}$$

ahol $\displaystyle t$ a repülési idő. A fenti két egyenletből álló egyenletrendszerben $\displaystyle t$-t és $\displaystyle \alpha$-t tekintjük ismeretlennek, és a maximális $\displaystyle d$-t keressük, ami mellett létezik rájuk megoldás. A két ismeretlen közül $\displaystyle \alpha$-t ejtsük ki először a következőképpen: fejezzük ki az első egyenletből $\displaystyle \cos\alpha$-t, a másodikból $\displaystyle \sin\alpha$-t:

$$\begin{align*} \cos\alpha&=\frac{d}{\sqrt{2gh}t},\\ \sin\alpha&=\frac{\frac{1}{2}gt^2-h}{\sqrt{2gh}t}. \end{align*}$$

Ezután a $\displaystyle \sin^2\alpha+\cos^2\alpha=1$ azonosságot alkalmazva kiküszöböljük az $\displaystyle \alpha$ ismeretlent:

$\displaystyle \left(\frac{\frac{1}{2}gt^2-h}{\sqrt{2gh}t}\right)^2+\left(\frac{d}{\sqrt{2gh}t}\right)^2=1,$

amit kicsit átrendezve az I. megoldás induló egyenletéhez jutunk.

Statisztika:

A P. 5571. feladat értékelése még nem fejeződött be.

A KöMaL 2024. májusi fizika feladatai

Már regisztráltál?
Új vendég vagy?