 |
Az S. 110. feladat (2016. október) |
S. 110. Peti pénztárcájában \(\displaystyle N\) darab pénzérme van, az \(\displaystyle i\)-ediknek az értéke \(\displaystyle e[i]\). Peti szeretne venni egy gombóc fagyit, de nem emlékszik rá, hogy pontosan mennyibe kerül, csak arra, hogy \(\displaystyle K\) krajcárnál biztosan nem lehet drágább (és az ára krajcárban kifejezve pozitív egész szám). Szeretné tudni, hogy pontosan (visszajáró nélkül) ki tud-e fizetni egy gombóc fagyit, ha csak az első \(\displaystyle R\) darab pénzérmét használja fel, akármennyi is legyen a fagyi ára. Segítsünk Petinek.
A standard bemenet első sora a kérdések \(\displaystyle Q\) számát és a pénzérmék \(\displaystyle N\) számát tartalmazza. A második sor \(\displaystyle N\) egész számot tartalmaz, a pénztárca tartalmát, az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik pénzérme \(\displaystyle e[i]\) értéke. Ezután következik a \(\displaystyle Q\) kérdés leírása, minden kérdés külön sorban: a kérdéses \(\displaystyle K\) maximális összeg, és az \(\displaystyle R\) szám.
A standard kimenet \(\displaystyle s\)-edik sora az \(\displaystyle s\)-edik kérdésre adott válasz: ha minden \(\displaystyle K\)-nál nem drágább fagyi pontosan kifizethető az első \(\displaystyle R\) darab érme fölhasználásával, akkor IGEN, egyébként a NEM szó kerüljön a sorba.
Korlátok: \(\displaystyle 1\le Q\le 10^5\), \(\displaystyle 1\le N\le 10^5\), \(\displaystyle 1\le K\le 10^{18}\), \(\displaystyle 1\le R\le N\), \(\displaystyle 1\le e[i]\le 10^9\), időlimit: 1 mp, memórialimit: 256 MB.
Pontozás: Az első 2 tesztesetben \(\displaystyle N\le 1000\) és \(\displaystyle K\le 1000\) (2 pontért);
A következő 3 tesztesetben az összes kérdésben \(\displaystyle R=N\) (további 3 pontért).
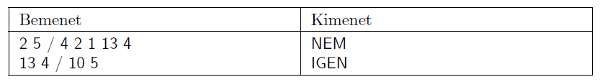
Magyarázat.
Első kérdés: például 12 krajcárt sehogyan sem lehet kifizetni az első négy pénzérmével.
Második kérdés: \(\displaystyle \mathbf{1}=1\), \(\displaystyle \mathbf{2}=2\), \(\displaystyle \mathbf{3}=2+1\), \(\displaystyle \mathbf{4}=4\), \(\displaystyle \mathbf{5}=4+1\), \(\displaystyle \mathbf{6}=4+2\), \(\displaystyle \mathbf{7}=2+1+4\), \(\displaystyle \mathbf{8}=4+4\), \(\displaystyle \mathbf{9}=4+1+4\), \(\displaystyle \mathbf{10}=4+2+4\).
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített s110.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2016. november 10-én LEJÁRT.
Az első 2 pont megszerezhető a klasszikus pénzváltás probléma megoldásával (dinamikus programozás, \(\displaystyle O(N\cdot K)\)).
A következő 3 pont megszerzéséhez a következő megfigyelésre van szükségünk:
Ha növekvő sorrendbe rendezzük a pénzérméket, akkor ha \(\displaystyle k\) pénzérme után a legkisebb (pontosan) nem kifizethető összeg \(\displaystyle m_k\), és minden ennél nagyobb összeg kifizethető, akkor
ha \(\displaystyle e[k+1] > m_k\), akkor \(\displaystyle m_{k+1} = m_k\) továbbra is a legkisebb nem kifizethető érték, és ezután minden \(\displaystyle l>k\)-ra \(\displaystyle e[l] > m_k\), vagyis \(\displaystyle m_k\) továbbra sem kifizethető, így \(\displaystyle m_l = m_k\), vagyis az összes érmével nem kifizethető legkisebb összeg \(\displaystyle m_n = m_k\).
különben \(\displaystyle e[k+1] \leq m_k\), és mivel minden \(\displaystyle m_k\)-nál kisebb \(\displaystyle o\) összeg kifizethető az első \(\displaystyle k\) érmével, \(\displaystyle o+e[k+1]\) kifizethető az első \(\displaystyle k+1\) érmével, így minden \(\displaystyle m_k+e[k+1]\)-nél kisebb összeg kifizethető lesz. De mivel az előző pontban leírtak alapján az összes eddigi érmével ugyanez volt a helyzet, \(\displaystyle e[1] + e[2] + \ldots + e[k] + e[k+1] = m_k-1 + e[k+1] = m_{k+1} - 1\), ahol \(\displaystyle m_{k+1} = m_k + e[k+1]\) (ezt teljes indukcióval bizonyíthatjuk). Viszont akkor \(\displaystyle m_{k+1}\) tényleg nem fizethető ki (mivel az összes eddigi érme összege kisebb, így egyszerűen nincs ennyi pénzünk).
A fenti feltételeket figyelembevéve kiszámíthatjuk \(\displaystyle m_n \)-t, és így minden \(\displaystyle m_n\)-nél nagyobb vagy egyenlő összegre NEM a válasz, minden \(\displaystyle m_n\)-nél kisebb összegre IGEN a válasz.
A mintamegoldás \(\displaystyle m_n - 1\)-et számolja ki.
A teljes pontszámért az előző módszert kell általánosítanunk. Itt nem rendezhetjük az érméket. Ehelyett szintén ki fogjuk számolni \(\displaystyle m_k\)-t minden \(\displaystyle k\)-ra, viszont a fel nem használt érméket (amelyek túl nagyok voltak), ``félrarakjuk", amíg túl nagyok. Erre a célra egy olyan adatszerkezet kell, amibe beilleszthetünk elemeket, illetve kivehetjük a legkisebbet hatékonyan. Ilyen adatszerkezet a kupac és a bináris keresőfa (implementációk: heap, set, priorityqueue; viszont kupacot magunk is implementálhatunk). Mivel minden érmét maximum egyszer adunk az adatszerkezethez, illetve maximum egyszer törlünk, összesen \(\displaystyle 2\cdot N\) műveletet végzünk az adatszerkezeten, így kellően hatékony implementációt használva \(\displaystyle O(N\cdot log(N))\) futási idő, és \(\displaystyle O(N)\) memóriahasználat elérhető.
Statisztika:
15 dolgozat érkezett. 10 pontot kapott: Busa 423 Máté, Csenger Géza, Kiss Gergely, Németh 123 Balázs, Noszály Áron. 7 pontot kapott: 1 versenyző. 6 pontot kapott: 2 versenyző. 5 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2016. októberi informatika feladatai
