 |
Az S. 111. feladat (2016. november) |
S. 111. Egy vasútállomáson különböző befogadóképességű személyvagonokból állítanak össze egy szerelvényt. Egy csapat katona az éppen rendezés alatt álló vonatra szeretne felszállni, ezért figyelik, ahogy a vagonokat tologatják. Megfigyelték, hogy a rendező mozdony egyszerre mindig csak egy kocsit mozgat, azaz a fő szerelvény egy helyben áll, és ennek a végére kapcsolhatnak egy vagont, illetve néha meggondolják magukat, ekkor le is kapcsolhatnak egy kocsit a szerelvény végéről vagy az elejéről. Továbbá minden vagonra rá van írva, hogy hány utas fér el benne (egy pozitív egész szám 1 és \(\displaystyle 10^9\) között). Egy tiszt figyeli a vonat összeállítását, és minden mozgatás után szeretné tudni, hogy mekkora osztagokat hozzon létre, ha minden osztag ugyanannyi katonából áll, és úgy kell felszállniuk a vonatra, hogy minden kocsi tele legyen, és az egyes osztagok tagjai ugyanabban a kocsiban utazzanak, továbbá minél kevesebb osztagba szeretné szervezni a katonákat. Mivel az állomáson rengeteg vagon van, ezért lapunk segítségét kérte, hogy ki tudja adni a helyes parancsokat.
A standard bemenet első sorában a mozgatások \(\displaystyle N\) száma van, a következő \(\displaystyle N\) sor mindegyike egy-egy mozgatást ír le:
\(\displaystyle \bullet\) 0 x \(\displaystyle \to\) új vagont kapcsolnak a szerelvény végére, aminek a kapacitása \(\displaystyle x\);
\(\displaystyle \bullet\) 1 \(\displaystyle \to\) lekapcsolják az utolsó vagont;
\(\displaystyle \bullet\) 2 \(\displaystyle \to\) lekapcsolják az első vagont. A standard kimenet \(\displaystyle N\) sort tartalmazzon, minden mozgatás után az osztagok méretét. Amennyiben a szerelvény az egyik mozgatás után üres lenne, akkor sajnos nem lehet létrehozni semekkora csapatokat sem, ezt a 0 szám kiírásával jelezzük. A mozgatások helyesek, vagyis üres szerelvényről sohasem kapcsolnak le kocsit. A szerelvény kezdetben üres.
Pontozás: az első két tesztesetben (2 pont) csak ,,0'' és ,,1'' típusú mozgatások vannak, vagyis a vonat elejét sosem kapcsolják le.
Korlátok: \(\displaystyle 1\le N\le 10^{5}\), időkorlát 1 mp, memórialimit: 256 MB.
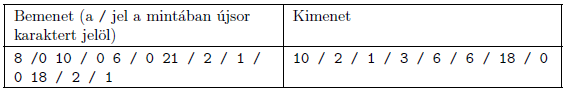
Magyarázat: a szerelvény az egyes műveletek után: (10); \(\displaystyle (10,6)\); \(\displaystyle (10,6,21)\); \(\displaystyle (6,21)\); (6); \(\displaystyle (6,18)\); (18); ().
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített s111.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2016. december 12-én LEJÁRT.
A feladat szövegét értelmezve kiderül, hogy valójában mi a feladat: minden szerelvényre meg kell adni a vagonok kapacitásának legnagyobb közös osztóját.
A legnagyobb közös osztót (lnko) az euklidészi algoritmus segítségével \(\displaystyle O(log(N))\) időben számolhatjuk (lásd a minta kódot).
Az első 2 pont megszerezhető, ha megfigyeljük, hogy \(\displaystyle lnko(a_1,...,a_{k-1},a_k) = lnko(lnko(a_1,...,a_{k-1}),a_k))\) a legnagyobb közös osztó asszociatív (csoportosítható) tulajdonsága miatt, illetve azt, hogy a vonat ebben az esetben veremként működik (hiszen csak az egyik végéhez kapcsolunk, illetve csak onnan kapcsolunk le vagonokat, egyesével). Így az ötlet az, hogy tároljuk egy veremben a legnagyobb közös osztókat. Ha jön egy új vagon, akkor annak a kapacitásának és a verem tetejének legnagyobb közös osztóját beszúrjuk a verem tetejére. Ha egy vagont lekapcsolnak, akkor eltávolítjuk a verem tetejét. így a válasz mindig a verem tetején lesz. Ha ügyesek vagyunk, rájöhetünk, hogy azt az esetet, amikor a vonat üres (a verem üres) könnyen kezelhetjük, ha eredetileg egy egyetlen 0 értéket tartalmazó veremmel indulunk (így az üres verem helyett mindig egy 0-t tartalmazó vermet kapunk, egyébként nem módosítja a választ).
A további 8 pont megszerzéséhez másképp kell hozzáállni a feladathoz. Először is vegyük észre, hogy ha egy vagon kapacitását 0-ra átírjuk, az olyan, mintha lekapcsoltuk volna (nem befolyásolja a legnagyobb közös osztót). A második fontos megfigyelés az, hogy maximum \(\displaystyle N\)-szer kapcsolunk a szerelvényhez új vagont, így az összhossz maximum \(\displaystyle N\) a lekapcsolt vagonokkal együtt.
Ezeket kihasználva ha egy csupa nullát tartalmazó tömbbel indulunk és mindig meg tudjuk találni a lekapcsolandó vagon indexét, akkor a feladat a következő lesz: Van egy tömbünk, ebben átírhatunk egy tetszőleges elemet, illetve lekérdezhetjük az egész tömb legnagyobb közös osztóját. Ez a szegmensfa klasszikus alkalmazása (ahol a szegmensfa művelete nyilvánvalóan a legnagyobb közös osztó).
Ennek tudatában az első részfeladat megoldását kiterjeszthetjük: Egy kétvégű sort (deque) kell fenntartani a tömbben, illetve egy szegmensfát építeni rá. Ezt könnyen megtehetjük két mutatóval (indexxel), amik a szerelvény első és utolsó vagonjára mutatnak.
A pontos megvalósításhoz lásd a mintamegoldást:
Minta 10 pontért (szegmensfa pointer-ekkel)
Statisztika:
17 dolgozat érkezett. 10 pontot kapott: Csenger Géza, Csertán András, Dóczi András, Gáspár Attila, Horváth Botond István, Janzer Orsolya Lili, Kiss Gergely, Nagy Nándor, Németh 123 Balázs, Noszály Áron, Vári-Kakas Andor. 9 pontot kapott: Tóth 827 Balázs. 8 pontot kapott: 1 versenyző. 6 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2016. novemberi informatika feladatai
