Az S. 112. feladat (2016. december)

S. 112. Egy város úthálózata párhuzamos sugárutakból és ezekre merőleges, egymással párhuzamos utcákból áll. A szomszédos utcák távolsága 100 méter, ahogyan a szomszédos sugárutaké is. Az egyszerűség kedvéért az utcákat sorban 1-től \(\displaystyle N\)-ig, míg a sugárutakat szintén sorban 1-től \(\displaystyle M\)-ig megszámozták. A városban nagy problémát jelent, hogy nincs tűzoltóság, így a városvezetés elhatározta, hogy épít egy tűzoltó központot. A központ épületének tervei már el is készültek, így tudjuk, hogy a tűzoltóautók az egyik útkereszteződésnél fognak kihajtani. A városban a tűzoltást tűzcsapok segítik, melyeket \(\displaystyle K\) darab kijelölt kereszteződésbe el is helyeztek. Minden tűzcsapnak tudjuk a helyét, illetve azt, hogy mennyire gyakori az, hogy a közelében tűz üt ki (\(\displaystyle p_{i}\) egész szám a tűz gyakoriságát jelöli az \(\displaystyle i\)-edik kereszteződés közelében). Ha tűz üt ki valahol, akkor a tűzoltóautók állandó sebességgel rögtön elindulnak a megfelelő tűzcsaphoz, csak utcákat és sugárutakat használva, a lehető legrövidebb úton. Úgy szeretnék kiválasztani a központ helyét, hogy a tűzesetekre való kiérkezési idő várható értéke minimális legyen. Ez akkor teljesül, ha \(\displaystyle \sum_1^K p_{i}\cdot d_{i}\) minimális, ahol \(\displaystyle d_{i}\) az \(\displaystyle i\)-edik tűzcsap és a központ távolsága. Készítsünk programot, amely megadja a legkedvezőbb útkereszteződés helyét.

A standard bemenet első sora az utcák \(\displaystyle N\) számát és a sugárutak \(\displaystyle M\) számát, illetve a tűzcsapok \(\displaystyle K\) számát tartalmazza. Az ezután következő \(\displaystyle K\) sor egy-egy tűzcsap pozícióját, illetve a tűz gyakoriságát írja le; minden sor három egész számot tartalmaz: az első az utca, a második a sugárút száma, a harmadik a gyakoriság.

A standard kimenet első és egyetlen sorába a tűzoltóság tervezett helye kerüljön, vagyis két egész szám jelölje a kihajtó helyét: az első az utca, a második a sugárút sorszámát. Több megoldás esetén bármelyik megadható.

Korlátok: \(\displaystyle 1\le N,M\le 10^{9}\), \(\displaystyle 1\le K\le 10^{5}\), \(\displaystyle 1\le p_{i}\le 100\). Időlimit: 0,1 mp. Memórialimit: 256 MB. A verem (stack) méretére nincs külön korlát, de a teljes memórialimitbe számít bele.

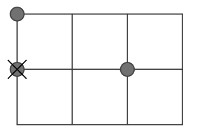
Az ábra a mintát tartalmazza, a körök a tűzcsapok, az \(\displaystyle X\) a tűzoltóság optimális helye.

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.

Beküldendő egy tömörített s112.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2017. január 10-én LEJÁRT.

A sugárutak egymásra merőlegesek, az egész várost elhelyezhetjük egy koordinátarendszerben és tekinthetünk rá úgy, mint pontok halmazára. A tűzoltóautó a városban a sugárutak mentén tud haladni, így az összes ponttól vett súlyozott Manhattan-távolságot szeretnénk minimalizálni. (Két pont Manhattan-távolsága a megfelelő koordinátáik különbségének összege: \(\displaystyle M=|x1-x2|+|y1-y2|\) ).

A képletből látszik, hogy a minimumszámolást megtehetjük külön-külön az \(\displaystyle x\) és az \(\displaystyle y\) koordinátákra. A tűzoltóállomás oszlopában és sorában is kell lennie tűzcsapnak, különben a sor/oszlop mozgatásával csökkenthető lenne a minimum, azaz csak az előforduló \(\displaystyle x\) illetve \(\displaystyle y\) koordinátákra kell kiszámolni a koordináták súlyozott mediánját.

Az algoritmusunk komplexitása \(\displaystyle O(K*log(K))\) a rendezés miatt, memóriaigénye O(K).

Megoldás: Busa Máté kódja main.cpp

Statisztika:

16 dolgozat érkezett.
10 pontot kapott:	Busa 423 Máté, Csenger Géza, Gáspár Attila, Janzer Orsolya Lili, Kiss Gergely, Molnár Bálint, Németh 123 Balázs.
9 pontot kapott:	Tóth 827 Balázs.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. decemberi informatika feladatai