Az S. 113. feladat (2017. január)

S. 113. Egy állatkertben egy hosszú, egyirányú sétálóutca egyik oldalán található sorban mind az \(\displaystyle N\) állat kifutója. Az állatkert a világon előforduló összes állatfajt egy 1 és \(\displaystyle 10^9\) közötti egyedi (egész) számmal azonosítja. Tudjuk, hogy sorban az \(\displaystyle N\) kifutó közül melyikben milyen állat van. Az állatkert speciális túrákat tart. Minden túra résztvevői két tetszőleges kifutó között megtekinthetik az összes állatot. A túra során elengedhetetlen, hogy a látogatók minden, az állatkertben megtalálható állatfajnak legalább egy egyedét láthassák. Az állatkert vezetése kíváncsi, hogy hányféle különböző túrát lehet az állatkertben vezetni ennek a feltételnek a betartásával. Két túra különböző, ha a kezdőpontjuk vagy a végpontjuk különböző. A sétálóutca egyirányú, tehát a résztvevők nem sétálhatnak visszafelé. Készítsünk programot, amely megadja a feltételnek eleget tevő túrák számát.

A standard bemenet első sorában a kifutók \(\displaystyle N\) száma van, a következő sor tartalmazza a kifutók ,,lakóinak'' azonosítóját sorrendben.

A standard kimenet egyetlen egész számot tartalmazzon: a különböző túrák számát.

Pontozás: Az első két tesztesetben \(\displaystyle N\le 100\), a harmadik tesztesetben \(\displaystyle N\le 5000\).

Korlátok: \(\displaystyle 1\le N\le 2\cdot 10^5\), minden állatfaj azonosítója 1 és \(\displaystyle 10^9\) közötti egész, az időkorlát 1 mp.

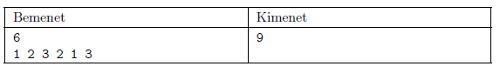
Magyarázat: a helyes túrák (kezdőponttal és végponttal megadva): (1,3), (1,4), (1,5), (1,6), (2,5), (2,6), (3,5), (3,6), (4,6).

(10 pont)

A beküldési határidő 2017. február 10-én LEJÁRT.

Megállapíthatjuk, hogy ha egy túra kezdő- és végpontja közt megtalálható az összes állat, akkor az összes olyan túra is jó, aminek a kezdőpontja ugyanaz, a végpontja pedig nagyobb. Azaz keressük meg az első elemtől induló túrához az első, feltételeknek megfelelő végpontot. Ha a kezdőpont helyét növeljük, akkor az első lehetséges végpont helye biztosan nem csökken, hiszen

-ha a kezdet növelésével a talált túra során van még ugyanolyan állat, akkor marad a végpont,

-ha nincs, akkor csak továbblépegetve találhatjuk meg az elejéről kieső állatot. Ha elérjük az állatkert végét, akkor nincs több megoldás.

Minden állatfajról tároljuk el, hogy milyen indexű helyeken fordul elő (\(\displaystyle VECTOR\)). Minden állatfajtánál az első indexet a fajtával együtt tegyük be egy \(\displaystyle SET\)-be, ami hely szerint rendez. Ekkor a túrák száma (\(\displaystyle N-az~utolsó~előforduló~index+1\)). Majd vegyük ki a \(\displaystyle SET\) első elemét és az így kieső állatfajt a következő előfordulási helyével tegyük vissza. Az eljárás akkor ér véget, ha a kivett állatfajnak már nincs további előfordulása.

Az algoritmus futásideje \(\displaystyle O(N*log(N))\).

Statisztika:

16 dolgozat érkezett.
10 pontot kapott:	Busa 423 Máté, Csenger Géza, Csertán András, Dóczi András, Gáspár Attila, Horváth Botond István, Janzer Orsolya Lili, Kiss Gergely, Molnár Bálint, Nagy Nándor, Németh 123 Balázs, Szakály Marcell, Vári-Kakas Andor.
8 pontot kapott:	1 versenyző.
7 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2017. januári informatika feladatai