Az S. 115. feladat (2017. március)

S. 115. A Piripócsi Általános Iskola diákjai egy vetélkedőn vesznek részt. A vetélkedő nagyon sok állomást tartalmaz, minden állomásnak van egy egyedi (pozitív egész) azonosítója. Minden állomáson a szervezők meg tudják mondani, hogy merre van a következő állomás. A diákok összesen legföljebb az állomások számának ötszöröse alkalommal kérdezhetnek rá a következő állomás számára. A gyerekeknél van egy térkép, ami alapján bármely állomásról bármely másik állomásra el tudnak jutni, az állomások távolsága nem fontos (nem is ismerjük). Minden állomáson van egy feladat, amit akkor oldanak meg, amikor először járnak az állomáson. A vetélkedő pályája az 1-es sorszámú állomásról indul, és egy adott \(\displaystyle j\) állomást akkor és csak akkor tartalmaz, ha \(\displaystyle j=1\), vagy van olyan \(\displaystyle i\) állomás a pályán, hogy \(\displaystyle i\) után \(\displaystyle j\) következik. A vetélkedőt akkor teljesítik sikeresen, ha minden, a pályán lévő állomáson megoldották a feladatot, viszont összesen az állomások számának ötszörösénél nem több kérdést tettek fel, illetve nem látogattak meg egyetlen, a pályán kívül lévő állomást sem. Természetesen megjegyezhetnek bizonyos válaszokat (de nem sokat), így nem kell mindig a következő állomásra menniük (lásd a példát).

Bemenet és kimenet: ez egy interaktív feladat. A program az értékelő környezettel a standard bemeneten és kimeneten keresztül kommunikálhat. A kommunikáció úgy zajlik, hogy a program feltesz egy kérdést, amire az értékelő válaszol: írjunk ki egyetlen pozitív egész számot, majd beolvashatjuk az arra az állomásra következő állomás sorszámát. Ha úgy gondoljuk, hogy teljesítettük a vetélkedőt, akkor írjunk ki egyetlen 0-t. Ezután azonnal fejezzük be a program végrehajtását, mást már ne írjunk ki. Fontos, hogy minden kiírás végén legyen sortörés.

Pontozás: 3 pontért a memórialimit 256 MB. A maradék 6 pontért a memórialimit 2 MB.

A memórialimitbe csak a feladathoz kapcsolódó adatok tárolására ténylegesen felhasznált memória számít bele.

Korlátok: A pályán maximum \(\displaystyle 10^7\) állomás van, az azonosítók 1 és \(\displaystyle 10^{18}\) közötti egész számok. Az időlimit 10 mp.

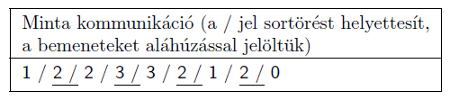
Magyarázat: a pálya \(\displaystyle \mathsf{1} \to \mathsf{2} \to \mathsf{3} \to \mathsf{2} \to \mathsf{3} \to \ldots,\) a megadott kérdések után minden állomáson jártak.

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.

Beküldendő egy tömörített s115.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2017. április 10-én LEJÁRT.

Statisztika:

9 dolgozat érkezett.
10 pontot kapott:	Busa 423 Máté, Gáspár Attila, Janzer Orsolya Lili, Kiss Gergely, Molnár Bálint, Noszály Áron, Tóth 827 Balázs, Vári-Kakas Andor.
9 pontot kapott:	Nagy Nándor.

A KöMaL 2017. márciusi informatika feladatai