 |
Az S. 116. feladat (2017. április) |
S. 116. Egy ország úthálózata kétirányú, egyenes autópályákból áll, melyek egy-egy várospárt kötnek össze. Minden útnak ismerjük a két végpontját, illetve a megtételéhez szükséges időt. Az országban két város (A és B) gyors fejlődésnek indult, így az ország vezetői minimalizálni szeretnék a két város közötti út megtételének idejét. Sajnos földrajzi okokból nem tudnak újabb autópályákat építeni. Kifejlesztettek egy közlekedési eszközt, egyenes számára kiépített speciális pályán elhanyagolható idő alatt (0) juttatja el a rakományát, vagy utasait a pálya két végpontja között. Mivel ez az új jármű nagyon drága, csak egyetlen darabot tudnak belőle megépíteni. A jármű vonalát csak egy már meglévő autópályával párhuzamosan lehet kiépíteni.
Írjunk programot, ami segít az ország vezetőinek megmondani, hogy melyik két város közötti autópálya mellé építsék ki a kifejlesztett közlekedési eszköz vonalát, illetve megmondja, hogy mennyivel csökken az utazási idő A és B között. A városokat 1 és \(\displaystyle N\) közötti sorszámokkal azonosítjuk.
A standard bemenet első sora a városok \(\displaystyle N\) számát és az autópályák \(\displaystyle M\) számát, illetve \(\displaystyle A\) és \(\displaystyle B\) sorszámát tartalmazza. A következő \(\displaystyle M\) sor egy-egy autópályát ír le, vagyis három egész számot tartalmaz szóközzel elválasztva: a két végpont sorszámát \(\displaystyle (x_{i},y_{i})\), illetve az adott autópálya megtételéhez szükséges időt (\(\displaystyle z_{i}\)-t) tartalmazza. Az A városból a B városba mindenképp el lehet jutni egy vagy több autópályán végighaladva. A standard kimenet első sorába írjuk ki, hogy maximum mennyivel csökkenthető az utazási idő A és B között, a második sorba pedig annak a két városnak sorszámát, amelyek között az új vonalat építeni kell.
| Bemenet (a / jel sortörést jelöl) | Kimenet |
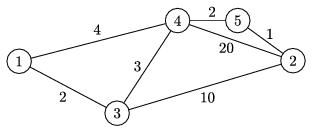
| 5 7 1 2 / 1 3 2 / 1 4 4 / 3 4 3 / 3 2 10 / 4 2 20 / 2 5 1 / 5 4 2 | 5 / 3 2 |
Magyarázat: az ábráról látszik, hogy a 3-as és 2-es pont közé építve a vonalat az utazási idő 7-ről 2-re csökken.
Korlátok: \(\displaystyle 2 \le N \le 100\,000\), \(\displaystyle 1 \le M \le 1\,000\,000\), \(\displaystyle 1 \le A\ne B \le N\), \(\displaystyle 1 \le x_{i}\ne y_{i} \le N\), \(\displaystyle 0 \le z_{i} \le 10\,000\). Az időlimit 1 mp, a memórialimit 256 MB. Az első két tesztesetben az előbbi korlátokon kívül teljesül, hogy \(\displaystyle M \le 1000\).
Pontozás: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített s116.zip állományban a program forráskódja (az .exe és más, a fordító által generált állományok nélkül), valamint a program rövid dokumentációja, amely leírja a megoldás menetét és megadja, hogy a forrás mely fejlesztői környezetben fordítható. Az utolsó két tesztesetre maximális pont csak akkor érhető el, ha a dokumentáció fent leírt bizonyítást tartalmazza.
(10 pont)
A beküldési határidő 2017. május 10-én LEJÁRT.
Futtassunk le egy-egy Dijkstra algoritmust \(\displaystyle A\) és \(\displaystyle B\) kezdőponttal. legyen \(\displaystyle d_A[p]\) a \(\displaystyle p\) pont távolsága \(\displaystyle A\)-tól, illetve \(\displaystyle d_B[p]\) hasonlóan a távolság \(\displaystyle B\)-től.
Ezután minden \(\displaystyle p-q\) autópályára, ha oda építjük az új vonalat, akkor az A-B utat háromféleképpen tehetjük meg:
1) Az új vonal használata nélkül, a távolság \(\displaystyle d_A[B]\).
2) \(\displaystyle A\)-ból \(\displaystyle p\)-be autópályákon, majd az új vonalon \(\displaystyle q\)-ba, majd onnan \(\displaystyle B\)-be autópályákon, ekkor a távolság \(\displaystyle d_A[p]+d_B[q]\).
3) \(\displaystyle A\)-ból \(\displaystyle q\)-ba autópályákon, majd az új vonalon \(\displaystyle p\)-be, majd onnan \(\displaystyle B\)-be autópályákon, ekkor a távolság \(\displaystyle d_A[q]+d_B[p]\).
Az összes élre megnézve mindhárom lehetőséget, könnyen kiválaszthatjuk az optimálisat, megjegyezve a (egy) élet, ami optimalizálja a távolságot. A kódolás során ügyeljünk arra, hogy ha a távolság nem rövidíthető (1. eset az optimális), akkor is helyes eredményt adjon a program.
A csatolt program minden optimális élet kilistáz a kitűzött feladattal ellentétben.
Alternatív megoldás, hogy minden várost két pontként tárolunk a gráfban: az elsőben akkor vagyunk, ha még nem használtuk az új eszközt, a másodikban pedig akkor, ha már igen. Ha ezt a modellt választjuk, akkor a feladat csak a Dijkstra algoritmus triviális alkalmazása.
Statisztika:
9 dolgozat érkezett. 10 pontot kapott: Busa 423 Máté, Kiss Gergely, Noszály Áron. 9 pontot kapott: Vári-Kakas Andor. 8 pontot kapott: 4 versenyző. 5 pontot kapott: 1 versenyző.
A KöMaL 2017. áprilisi informatika feladatai
