Az S. 119. feladat (2017. október)

S. 119. Ifjú hercegünk egy hegyi ösvényen készül átkelni. Az ösvény mentén manók állnak lesben, akikkel semmiképp nem jó találkozni. Szerencsére a manók mindegyike olyan, hogy egy bizonyos színt nem lát. Hercegünk ezért varratott magának mindegyik színből egy-egy köpenyt, így ha a megfelelő manó előtt elhaladva azt viseli, akkor a manó nem veszi észre. A köpenyek mindegyike karra terítve is könnyen vihető, és emellett tetszőleges számú köpeny – akár az összes – egymásra fölvéve hordható. Ha a herceg már visel egy vagy több köpenyt, akkor a következőt azok fölé tudja venni. Vetkőzéskor mindig a legfelső köpenyt tudja levenni, tehát ha szüksége van egy most nem legfelül viselt köpenyre, akkor az összes fölötte lévőt le kell vennie.

A herceg azt is megtudta, hogy milyen sorrendben következnek az egyes manók az ösvény mentén. Mivel nem szeretne sokszor öltözni, ezért szeretné tudni, hogy hogyan juthat túl a lehető legkevesebb számú öltözéssel az ösvényen. Az út megkezdése előtt nem viseli egyik köpenyt sem, és az ösvény után sem, tehát leveszi, ami még rajta van. Minden köpeny föl- vagy levétele egy öltözésnek számít.

A feladatot megoldó program olvassa be a standard bemenetről a manók \(\displaystyle N\) számát, illetve az általuk nem látott színek \(\displaystyle Z\) számát, majd a következő sorból \(\displaystyle N\) számú pozitív egészet: az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik manó által nem látott szín \(\displaystyle m_i\) sorszáma. A program írja a standard kimenetre az ösvényen való áthaladáshoz szükséges legkevesebb öltözések számát.

Példák:

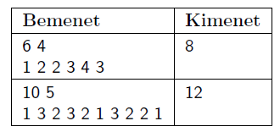
Korlátok: \(\displaystyle 1 \le Z \le N \le 30\), \(\displaystyle 1 \le m_i \le Z\).

Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb \(\displaystyle N\) értékek esetén ad helyes eredményt 1 másodpercen belül.

Beküldendő egy s119.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.

(10 pont)

A beküldési határidő 2017. november 10-én LEJÁRT.

A feladatra érkezett megoldások jelentős részében a versenyzők feltételezték, hogy valamely egyszerű szabályosság alapján következtetni lehet arra, hogy a következő köpeny felvétele előtt érdemes-e levenni a köpenyt, vagy sem. Sajnos – eddig – nem találtunk általános "képlet" arra, hogy egy adott helyzetben mit érdemes tenni. Így igazából az összes eset módszeres végigpróbálása maradt. Természetesen lehetett egyszerűsíteni helyzeteket, pl. ha egy köpeny színe még egyszer nem fordul elő, akkor nyilván levehető, vagy ha az egymást követő manók színei "palindom" helyzetűek, vagyis pl. 12321, akkor nyilván érdemes az 1 és 2 köpenyt nem levenni.

Nézzük az összes eset vizsgálatát. Mivel 30 manón kellett áthaladni, ezért – az utolsó kivételével – 29 helyen lehetett levenni vagy fölvenni a legfelső köpenyt. Így \(\displaystyle 2^{29}\) lehetőség adódik. (Nyilván lehetséges, hogy egy manó után több köpenyt vesz le a herceg, de az egyenértékű azzal, hogy a fölvétel után leveszi.) Ezek alapján egy \(\displaystyle 2^{29} \approx 1024^3 \approx 10^9\). Egy GHz-es processzorral dolgozó gépeken egy backtrack-es megoldás nem fut le 1s alatt, mert a köpenyek cserélgetését adminisztrálni kell a programban. Így a jó megoldáshoz részfeladatokra kellett bontani a teljes feladatot.

Mintamegoldásként Gáspár Attila miskolci (S119.cpp ), és Busa Máté (s119bm.cpp) nagykanizsai versenyző munkáját közöljük.

Tesztfájlok és helyes kimenetek: teszt.zip

Statisztika:

14 dolgozat érkezett.
10 pontot kapott:	Busa 423 Máté, Gáspár Attila.
7 pontot kapott:	4 versenyző.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	5 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.

A KöMaL 2017. októberi informatika feladatai