Az S. 126. feladat (2018. május)

S. 126. Általánosítsuk az idén februárban kitűzött C. 1466. feladatot. Egy bizottság összesen \(\displaystyle A\) alkalommal ülésezett. A tagok közül minden ülésen pontosan \(\displaystyle S\) személy vett részt, de bármely két tag legföljebb egyszer volt együtt jelen. Legalább hány tagból áll a bizottság?

A program a standard bemenet első sorából olvassa be az ülések \(\displaystyle A\) számát és az egy ülésen résztvevő személyek \(\displaystyle S\) számát. A program írja a standard kimenet első sorába, hogy legkevesebb hány tagból áll a bizottság.

Példa:

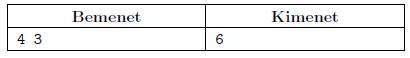
Korlátok: \(\displaystyle 3 \le S \le 10\), \(\displaystyle 3 \le A \le 12\).

Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb bemeneti értékek esetén ad helyes eredményt 1 másodpercen belül.

Beküldendő egy s126.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.

(10 pont)

A beküldési határidő 2018. június 11-én LEJÁRT.

Statisztika:

2 dolgozat érkezett.
4 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2018. májusi informatika feladatai