Az S. 130. feladat (2018. december)

S. 130. Az asztalon sorban előttünk van \(\displaystyle N\) darab kártya, mindegyiken egy egész számmal. Válasszuk ki a lehető legkevesebb egymás melletti számkártyát, amik közül a legnagyobb és a legkisebb különbsége legalább \(\displaystyle D\) (ilyen biztosan van).

Bemenet: az első sor a számkártyák \(\displaystyle N\) számát és a \(\displaystyle D\) számot tartalmazza. A következő sor a számkártyákon levő számokat tartalmazza sorban (a kártyákat 0-tól indexeljük). Több megoldás esetén a legkisebb kezdőindexű megoldást kell megadni.

Kimenet: egy sorba írjunk ki két számot: az első és az utolsó kiválasztott kártya indexét.

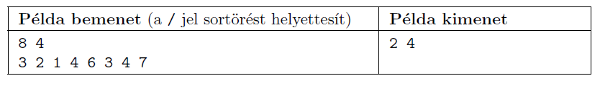
Korlátok: \(\displaystyle 0\le N\le 3\cdot {10}^{6}\), \(\displaystyle -{10}^{9}\le \text{számkártya számai}\le {10}^{9}\).

Időlimit: 0,5 mp, memórialimit: 100 MiB.

Értékelés: a pontok 20%-a kapható, hogyha \(\displaystyle N\le 100\); további 20% kapható, ha \(\displaystyle N\le 1000\); további 20% kapható, ha \(\displaystyle N\le {10}^{5}\); további 40% kapható az eredeti bemenetre.

Beküldendő egy s130.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy melyik fejlesztő környezetben futtatható.

Az I/S és S-jelű feladatok megoldását a http://mester.inf.elte.hu automatikus értékelő rendszer segítségével kipróbálhatod, tesztelheted (Téma: KöMaL - 2018/19).

(10 pont)

A beküldési határidő 2019. január 10-én LEJÁRT.

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:	Kiss Gergely, Molnár Bálint, Noszály Áron.
9 pontot kapott:	Csertán András, Gyimesi Péter, Szente Péter.
6 pontot kapott:	2 versenyző.

A KöMaL 2018. decemberi informatika feladatai