Az S. 134. feladat (2019. április)

S. 134. Szeretnénk új könyveket venni. Egy boltban \(\displaystyle N\) féle könyvet árusítanak, az \(\displaystyle i\)-ediket \(\displaystyle P_{i}\) forintért. Szerencsére rendelkezünk \(\displaystyle K\) darab kuponnal. Ha az \(\displaystyle i\)-edik könyv megvételekor elhasználunk egy kupont, akkor azt \(\displaystyle P_{i}\) helyett \(\displaystyle R_{i}\) forintért tudjuk megvásárolni. Egy könyvnél csak egy kupont tudunk elhasználni. Adjuk meg, hogy legföljebb hány könyvet tudunk megvásárolni \(\displaystyle M\) forintért.

A standard bemenet első sora tartalmazza az \(\displaystyle N\), \(\displaystyle K\), \(\displaystyle M\) számokat; a következő \(\displaystyle N\) darab sor tartalmazza a \(\displaystyle P_{i}\) és \(\displaystyle R_{i}\) számokat. A kimeneten adjuk meg, hogy legfeljebb hány könyvet tudunk megvenni.

Példa:

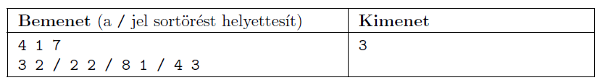
Korlátok: \(\displaystyle 1\le K\le N\le 50\,000\), \(\displaystyle 1\le M\le {10}^{14}\), \(\displaystyle 1\le R_{i}\le P_{i}\le {10}^{9}\). Időlimit: 0,5 mp.

Beküldendő egy s134.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztő környezetben futtatható.

(10 pont)

A beküldési határidő 2019. május 10-én LEJÁRT.

Statisztika:

3 dolgozat érkezett.
10 pontot kapott:	Noszály Áron.
6 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.

A KöMaL 2019. áprilisi informatika feladatai