 |
Az S. 143. feladat (2020. április) |
S. 143. Adott egy irányított gráf, amelynek \(\displaystyle N\) csúcsa és \(\displaystyle M\) éle van. Semelyik két csúcs közt sincs egynél több közvetlen él (iránytól függetlenül). Nevezzük körsétának a csúcsok egy olyan \(\displaystyle x_{1}, x_{2}, x_{n}\) sorozatát, ahol \(\displaystyle x_{1}=x_{n}\) és minden \(\displaystyle 1\le i\le n-1\) esetén létezik \(\displaystyle x_{i}\)-ből \(\displaystyle x_{i+1}\)-be mutató él, valamint a körséta során egy csúcson tetszőleges sokszor átmehetünk, de egy élen csak egyszer.
Legyen az ilyen körséták száma egy gráfban \(\displaystyle K\). Kérdés, hogy legföljebb hány irányított élt húzhatunk be a gráfba úgy, hogy a körséták száma továbbra is \(\displaystyle K\) legyen, és semelyik két csúcs között ne legyen egynél több közvetlen él (iránytól függetlenül). A csúcsokat 1-től indexeljük.
Bemenet: az első sor tartalmazza az \(\displaystyle N\) és \(\displaystyle M\) számot. A következő \(\displaystyle M\) sor mindegyike tartalmaz egy \(\displaystyle a_{i}\) és \(\displaystyle b_{i}\) számot, ami azt jelenti, hogy megy egy irányított él az \(\displaystyle a_{i}\) csúcsból a \(\displaystyle b_{i}\) csúcsba. Kimenet: adjuk meg a maximálisan behúzható élek számát.
Példa:
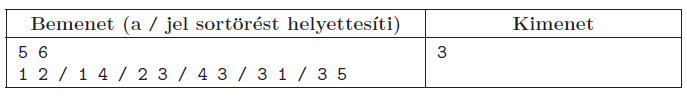
Korlátok: \(\displaystyle 1\le N,M\le {10}^{5}\). Időkorlát: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha \(\displaystyle N,M\le 100\).
Beküldendő egy s143.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Statisztika:
5 dolgozat érkezett. 10 pontot kapott: Horcsin Bálint, Noszály Áron, Szente Péter, Varga 256 Péter. 5 pontot kapott: 1 versenyző.
A KöMaL 2020. áprilisi informatika feladatai
