Az S. 169. feladat (2023. március)

S. 169. 2 egység magasságú egyenes hasáb alakú tárolóedényt szeretnénk készíteni. Az edény alapjának elkészítéséhez kiindulásként adott egy konvex sokszög, melynek csúcsai a koordináta-rendszer rácspontjaira esnek. Ennek a sokszögnek töröljük egy csúcsát és a csúcshoz kapcsolódó két élét, és összekötjük egy éllel a törölt élek megmaradt csúcspontjait. Az így kialakuló sokszöget tekintjük a tárolóedény alapjának.

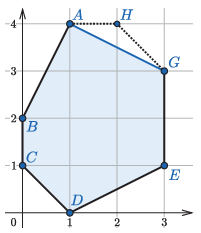
Feladatunk, hogy a feltételek szerint adott konvex sokszög esetén határozzuk meg, mekkora a belőle készíthető legnagyobb kapacitású edény kapacitása.

A bemenet első sorában a konvex sokszög csúcsainak \(\displaystyle N\) száma szerepel. A következő \(\displaystyle N\) sorban a csúcsok \(\displaystyle x\) és \(\displaystyle y\) koordinátája pozitív körüljárási irány szerint. A listában a szomszédos pontok a sokszöget alkotó szakaszok végpontjai. Az első és az utolsó csúcs is össze van kötve.

A kimenet első és egyetlen sorába a konvex sokszögből készíthető legnagyobb kapacitású edény kapacitása kerüljön.

Minta:

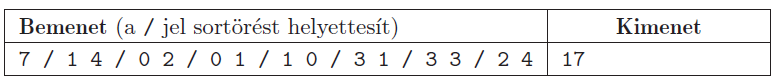
Magyarázat: az ábrán a \(\displaystyle H\) csúcsot törölve az edény kapacitása 17.

Korlátok: \(\displaystyle 1\le N \le 100\,000\), \(\displaystyle -10^8\le x,y \le 10^8\). Időkorlát: 1 mp.

Értékelés: A pontok 40%-a kapható, ha a program helyes kimenetet ad az \(\displaystyle {N\le 100}\) esetekben.

Beküldendő egy s169.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

A beküldési határidő 2023. április 17-én LEJÁRT.

Statisztika:

3 dolgozat érkezett.
10 pontot kapott:	Horváth Milán, Puppi Barna, Zádor-Nagy Zsombor.

A KöMaL 2023. márciusi informatika feladatai