Az S. 170. feladat (2023. április)

S. 170. Bergengóciában télen minden éjszaka leesik valamennyi hó, nappal viszont az összes meglévő hó fele elolvad. Ki szeretnénk számolni minden nap, hogy egy Bergengóciát átszelő egyenes út egy szakaszán mennyi hó található. Tudjuk, hogy kezdetben nincs hó az úton és ismerjük, hogy minden éjszaka mennyi hó esett. Bergengócia hófelhői éjszaka nem mozognak, így minden felhő egyenletesen terít be hóval egy útszakaszt. Tudjuk még, hogy minden éjszaka csak egy felhőből esett hó. Számítsuk ki, mennyi hó maradt egy-egy nap estéjére a kérdezett szakaszon, miután a reggel még meglévő hó fele elolvadt, de még nem esett új hó.

A bemenet első sorában a napok száma, \(\displaystyle N\) szerepel. A következő \(\displaystyle N\) sorban az egyes napok havazásainak adatai és a vizsgált intervallum adatai szerepelnek. Az úton a \(\displaystyle k\) kezdő és \(\displaystyle v\) végpont, melyek között hó esett, illetve a leesett hó \(\displaystyle h\) mennyisége (ennyivel nő a hótakaró vastagsága az intervallumon). A következő két szám \(\displaystyle q1\) és \(\displaystyle q2\) a kérdezett útszakasz határa, amelyen kíváncsiak vagyunk a hótakaró térfogatára.

A kimenet \(\displaystyle N\) sort tartalmazzon: az \(\displaystyle i\)-edik sorba az \(\displaystyle i\)-edik nap estéjén az úton maradt hó térfogatát kell írni, ha az út szélessége egységnyi. Figyelem! Habár a bemenetben egész számok szerepelnek, az eredmény lehet tört érték, így azt legalább két tizedesjegy pontossággal kell kiírni.

Minta (a / jel sortörést helyettesít):

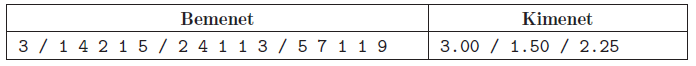
Magyarázat (a napok éjjel kezdődnek): első éjjel leesik \(\displaystyle 3\cdot 2=6\) egység hó, aminek a fele elolvad, így estére 3 egység hó lesz. A második éjszaka esik \(\displaystyle 2\cdot 1=2\) egység hó, így a második nap reggelére 5 egység hó marad, mely estére a felére olvad. A kérdezett intervallumba ebből csak 1,5 esik. A harmadik éjjelen \(\displaystyle 2\cdot 1=2\) egység hó esik, és marad még a korábbi hó fele, azaz 2,5 egység. A harmadik nap estéjére mindennek a fele marad, azaz 2,25 egység.

Korlátok: \(\displaystyle 1\le N \le 10\,000\), \(\displaystyle 0\le k, v, h, q1, q2 \le 108\). Időkorlát: 1 mp.

Értékelés: a pontok 40%-a kapható, ha a program helyes kimenetet ad az \(\displaystyle {N\le 100}\) esetekben.

Beküldendő egy s170.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

A beküldési határidő 2023. május 15-én LEJÁRT.

Statisztika:

3 dolgozat érkezett.
10 pontot kapott:	Horváth Milán, Szabó Imre Bence.
9 pontot kapott:	Volford Barnabás.

A KöMaL 2023. áprilisi informatika feladatai