 |
Az S. 49. feladat (2009. december) |
S. 49. Bergengócia környezettudatos ország. Azt tervezik, hogy a teherszállítást hidrogénnel hajtott járművekkel oldják meg. A hidrogént cseppfolyósítva lehet - a benzinhez hasonlóan - nagybiztonságú tárolótartályokból a teherautókba tölteni. Sajnos még kevés töltőállomás van. Hidrogén üzemanyagú teherszállítást ott lehet alkalmazni, ahol a hidrogénkutak legfeljebb \(\displaystyle K\) kilométer távolságban vannak egymástól.
A bergengócok pontosan nyilvántartják a hidrogénkutak koordinátáit. Két kút távolságán a koordináta-különbségek abszolút értékének összegét értik:
\(\displaystyle T= |x_1 -x_2|+ |y_1 -y_2|. \)
Segítsük a bergengóc teherszállítás tervezőit azzal, hogy a hidrogénkutakat csoportosítsuk. Két kutat egy csoportba teszünk, ha az egyiktől a másikig el lehet jutni a csoport kútjait érintve úgy, hogy az egymást követő kutak távolsága legfeljebb \(\displaystyle K\) kilométer.
Készítsünk programot, amely megadja, hogy a hidrogénkutak hány csoportot alkotnak és melyek tartoznak egy csoportba.
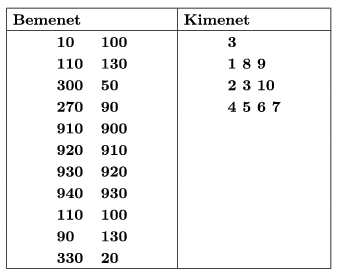
A program a parancssor első argumentumaként megadott bemeneti állomány első sorából beolvassa a hidrogénkutak \(\displaystyle N\) (\(\displaystyle 3\le N\le 200\)) számát, \(\displaystyle K\) (\(\displaystyle 100\le K\le 500\)) távolság értékét, majd a következő \(\displaystyle N\) sorból a kutak \(\displaystyle x\); \(\displaystyle y\) (\(\displaystyle 0\le x;y\le 1000)\) koordinátáit.
A parancssor második argumentumaként megadott kimeneti állomány első sorába írjuk a csoportok \(\displaystyle DB\) számát, majd a következő \(\displaystyle DB\) sorba az egy csoportba tartozó hidrogénkutak sorszámát szóközzel elválasztva.
Beküldendő egy tömörített állományban (s49.zip) a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét bemutató dokumentáció.
Forrásfájlok: S49teszt.zip
(10 pont)
A beküldési határidő 2010. január 11-én LEJÁRT.
Megoldásokról
Sok tökéletes megoldás érkezett a feladatra. A gráfok bejárását ismerőknek nem jelentett problémát a megoldás.
Mintamegoldás
Borsos Zalán (Marosvásárhely, Bolyai Farkas Elméleti Líceum, 11. osztály) megoldása alapján
A program kiszámítja minden kút pár közti távolságot (O(n2 ) ), majd a következő gondolatmenetet követi: legyen egy gráf, amelynek csúcspontjai az N darab töltőállomás. Él van az i és j töltőállomás között, ha köztük a távolság kisebb vagy egyenlő, mint k. A feladatunk így a gráf összefüggő komponenseinek a meghatározása, amelyet egy mélységi bejárással oldunk meg csúcs-szomszédsági mátrixból.
Statisztika:
19 dolgozat érkezett. 10 pontot kapott: Adrián Patrik, Borsos 607 Zalán, Éles András, Élő Dániel, Énekes Péter, Hunyady Márton, Iglói Gábor, Mokcsay 026 Ádám, Nagy 111 Miklós, Németh Bence, Ofella Norbert, Szabó 928 Attila, Weisz Ágoston, Weisz Gellért. 8 pontot kapott: 2 versenyző. 5 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2009. decemberi informatika feladatai
