 |
Az S. 60. feladat (2011. február) |
S. 60. Egy négyzet alakú földdarabból egy adott méretű, szintén négyzet alakú területet szeretnénk elkeríteni. A kerítéseknek párhuzamosaknak kell lenniük a földdarab oldalaival. Arra törekszünk, hogy minél több fa legyen az elkerített részben (a kerítés vonalára eső fákat úgy számoljuk, hogy belül vannak).
Írjunk programot, ami a standard bemenetről beolvassa a földdarab és az elkerítendő terület méretét, valamint a fák elhelyezkedését, és standard kimeneten megadja a kerítés egy optimális elhelyezését.
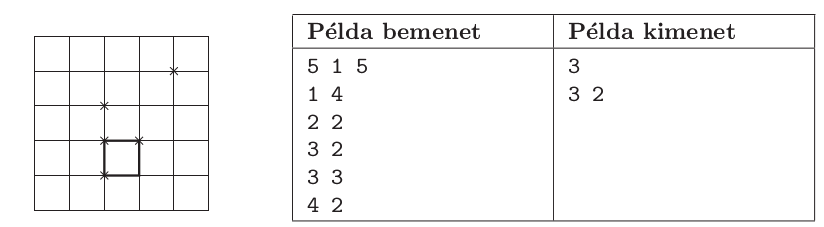
A bemenet szerkezete a következő: az első sorban három szóközzel elválasztott szám, a földdarab oldalhossza (\(\displaystyle 1 \le N \le 4000\)), az elkerítendő terület oldalhossza (\(\displaystyle 1 \le M \le N\)) és a fák száma (\(\displaystyle 1 \le K \le 1\;000\;000\)) található. A következő \(\displaystyle K\) sor mindegyikében szóközzel elválasztva egy-egy fa sor- és oszlopkoordinátái szerepelnek (\(\displaystyle 0 \le I, J \le N\)). Minden koordináta egész szám, és nincs két olyan fa, amelyeknek mindkét koordinátája megegyezik.
A standard kimenet első sorába írjuk ki az elkerített részbe kerülő fák számát, a második sorába pedig az elkerített négyzet bal felső sarkának sor- és oszlopkoordinátáit szóközzel elválasztva. Több megoldás esetén bármelyik megadható.
A futási időlimit tesztesetenként 10 másodperc.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció egy tömörített mappában.
(10 pont)
A beküldési határidő 2011. március 10-én LEJÁRT.
A feladatot dinamikus programozással lehetett megoldani. Mintamegoldásként Szabó Attila 10. osztályos pécsi tanuló megoldását közöljük. A kulcsgondolatot Borsos Zalán 12. osztályos marosvásárhelyi versenyző írta le a legvilágosabban (ábrát is mellékelve), így az ő dokumentációját is közzé tesszük.
Statisztika:
9 dolgozat érkezett. 10 pontot kapott: Nagy 111 Miklós, Nagy Róbert, Szabó 928 Attila. 9 pontot kapott: Borsos 607 Zalán. 5 pontot kapott: 2 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző.
A KöMaL 2011. februári informatika feladatai
