 |
Az S. 80. feladat (2013. április) |
S. 80. Gombóc Artúr sokat jár barátaihoz egy N lakosú városban. Az utcák egyirányúak a városban. Gombóc Artúr nem szeret sokat gyalogolni, így azon töprengett, hogy hány olyan utca van és melyek azok, amiken végigmehet úgy, hogy saját lakásától az egyik barátjához (N-1 barátja van, hiszen mindenki a barátja) sétál el az egyik legrövidebb úton. Miután ezen gondolkozott egy keveset, úgy döntött, ideje valami nehezebb munkába fogni, és a következő kérdést tette fel: ,,Hányféleképpen juthatok el a lakásomból az egyes barátaimhoz valamelyik legrövidebb úton?''
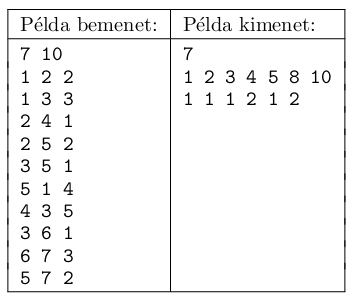
A program olvassa be a standard input első sorából N-et és M-et (): a lakások és az utcák számát, majd a következő M sorból a ki, vi, si szóközzel elválasztott egészeket: azaz a ki lakás kezdőpontú, vi lakás végpontú, si hosszú utcát. Gombóc Artúr lakása az 1. Írjuk a standard output első sorába az a egészet, ahol a db utca a válasz az első kérdésre, majd a következő sorba az a db utcát rendezve (a bemeneti állományban elfoglalt sorszámukkal azonosítva), növekvő sorrendben, szóközzel elválasztva. Az utolsó sorba pedig a második kérdésre válaszként minden barátjára ki kell írni, hogy hányféleképpen lehet oda valamely legrövidebb úton eljutni, illetve ennek a számnak az 1000007-es maradékát.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül. Kapható részpontszám a 9 pontból, ha a program csak kisebb tesztesetekre tud lefutni időben. A programra nem jár pont, ha az első részfeladatra a bemeneteknek legalább 20%-ánál nem ad helyes kimenetet.
Beküldendő egy tömörített s80.zip állományban a program forráskódja (s80.pas, s80.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s80.txt, s80.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2013. május 10-én LEJÁRT.
Megoldás
A Dijkstra algoritmussal megkeressük a kezdőpontból az összes minimális távolságot: d(v). Ezután definiáljuk pontos éleknek azokat az uv éleket, melyekre d(v)-d(u)=s(uv), ahol s(uv) az uv él hossza. Miért is jó ez, illetve mit is jelent ez? Azt jelenti, hogy ha ezen az élen végigmegyünk, akkor ha az u pontig egy minimális úton mentünk, akkor hozzátéve ezt az élet szintén minimális utat kapunk, mert a Dijkstra a minimális távolságokat adta meg, és az egyenlőség miatt pont ezt kapjuk az utunk hosszának. Tehát a pontos élek lesznek a megoldás az első kérdésre. Már csak a második kérdésre kell válaszolni. Vegyük a pontos élek részgráfját. Ugye ha nem pontos élen megyünk, akkor az egyenlőség nem teljesül, emiatt nem kaphatunk minimális utat. Így már csak azt kell eldönteni, hogy ebben a részgráfban a kezdőponttól az egyes pontokig hányféleképpen juthatunk el. Ezt többféleképp is megoldhatjuk: topologikusan rendezzük a csúcsokat (a gráf körmentes, mert ha lenne benne kör pontos élekből, akkor minden él súlya 0 kellene, hogy legyen), majd sorrendben végigmegyünk rajtuk. Ekkor könnyen frissíthetjük, hogy az aktuális csúcsba hányféleképp juthatunk el, hiszen csakis az őt megelőzőekből juthatunk el oda (topologikus rendezés miatt), azt meg már kiszámoltuk. Pontosabban az összes bele mutató él kezdőpontján kell összeadnunk a számokat.
Mi is az a topologikus rendezés? Van egy körmentes irányított gráfunk. Szeretnénk úgy sorba rendezni a csúcsokat, hogy csak jobbra mutassanak az élek. Erre a következő az algoritmus: mélységi bejárással elhagyási idő szerint (amikor már az összes leszármazottját bejártuk) rendezzük a csúcsokat. Ez pont jó lesz.
Mintamegoldás: main.cpp
Statisztika:
6 dolgozat érkezett. 10 pontot kapott: Szabó 928 Attila. 8 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2013. áprilisi informatika feladatai
