Az S. 87. feladat (2014. február)

S. 87. Az Újító Matematikusok Közössége egy új definíciót alkotott. Ezentúl egy természetes számokból álló véges sorozat Újított Legnagyobb Közös Osztóját, röviden ÚLNKO-ját a következőképpen határozzák meg: veszik a sorozat elemszámát, és megszorozzák a sorozat elemeinek régi, elavult típusú legnagyobb közös osztójával. Ez a szám lesz a sorozat ÚLNKO-ja. Rögtön kaptunk tőlük egy feladatot: adott egy (a₁,...,a_N) pozitív egészekből álló sorozat (). Adjuk meg az összes összefüggő (szomszédos elemekből álló) részsorozat ÚLNKO-jának maximumát.

A program olvassa be a standard input első sorából N-et, majd a következő sorból az a_i számokat (1a_i10¹¹). Írja a standard output első és egyetlen sorába azt a legnagyobb elérhető pozitív egészet, melyet egy összefüggő részsorozat ÚLNKO-jaként kapunk.

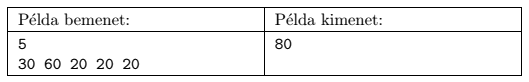
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül. Részpontszámok kaphatóak, ha a program N200-ra megoldást ad, illetve ha N5000-re megoldást ad.

Beküldendő egy tömörített s87.zip állományban a program forráskódja (s87.pas, s87.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s87.txt, s87.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2014. március 10-én LEJÁRT.

Mintamegoldásnak Somogyvári Kristóf megoldását tesszük közzé. A feladatnak ez az ismert leggyorsabb megoldása, intervallumfával - okosan lehet kicsit lassabbat, illetve nem olyan nagyon okosan kb 10-ed ilyen lassút. S87.zip

Statisztika:

15 dolgozat érkezett.
9 pontot kapott:	Weisz Ambrus.
7 pontot kapott:	1 versenyző.
5 pontot kapott:	4 versenyző.
4 pontot kapott:	3 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2014. februári informatika feladatai