Az S. 92. feladat (2014. október)

S. 92. Adott \(\displaystyle N\) (\(\displaystyle 1\le N\le 2\;000\;000\)) db nem feltétlenül különböző egész számunk egy sorozatban, melyek mindegyike 1 és 1000000000 között van. Válasszunk ki adott \(\displaystyle K\) számú (\(\displaystyle 1\le K\le N\)) különböző egészet a sorozatból úgy, hogy törölve a kiválasztott számokat és azok összes többi előfordulását, a lehető leghosszabb azonos számokból álló összefüggő részsorozat szerepeljen a megmaradt számokat tartalmazó sorozatban.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle K\)-t, majd a következő sorból a sorozat tagjait, majd írja a standard output első sorába a leghosszabb elérhető részsorozat hosszát.

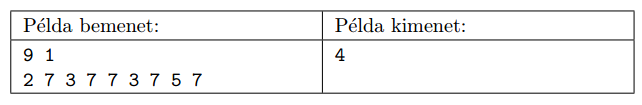
Magyarázat a példához: ha töröljük az összes 3-ast a sorozatból, akkor a következőt kapjuk: 2 7 7 7 7 5 7, itt nyilván 4 db egymás utáni 7-es a leghosszabb. Ha más számot törölnénk, akkor sem fordulna elő ennél hosszabb azonos számokból álló összefüggő részsorozat a visszamaradt sorozatban.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Beküldendő egy tömörített s92.zip állományban a program forráskódja (s92.pas, s92.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s92.txt, s92.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2014. november 10-én LEJÁRT.

Mintamegoldásként Németh Balázs megoldását közöljük: S92.zip

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Csenger Géza, Gáspár Attila, Németh 123 Balázs, Weisz Ambrus.
9 pontot kapott:	Zarándy Álmos.
6 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2014. októberi informatika feladatai