A KöMaL 2024. májusi matematika feladatai

K-jelű feladatok A beküldési határidő 2024. június 10-én LEJÁRT.

---

K. 814. Egy mezőn birkanyáj legelészik. A birkák egy részét megjelölték, a megjelölt és a jelöletlen birkák számának aránya \(\displaystyle \dfrac{3}{5}\).

A jelöletlen birkák közül csak \(\displaystyle 17\) van megnyírva, a megjelölt birkákat mind megnyírták, viszont a megnyírt és a meg nem nyírt birkák száma egyenlő. Hány birka legelészik a réten?

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

K. 815. Az \(\displaystyle ABC\) derékszögű háromszög \(\displaystyle BC\) befogóján úgy vettük fel a \(\displaystyle D\) pontot, hogy \(\displaystyle BC=4BD\), az \(\displaystyle AC\) befogón felvett \(\displaystyle E\) pontra pedig \(\displaystyle AC=8CE\) teljesül.
Határozzuk meg az \(\displaystyle AB\) átfogó hosszát, ha tudjuk, hogy \(\displaystyle AD=164\) és \(\displaystyle BE=52\).

vietnámi feladat

(5 pont)

megoldás, statisztika

---

K. 816. Adott az \(\displaystyle {E(x)=\dfrac{8x-12}{4x^2-12x+9}-\dfrac{5x}{2x^2+3x}-\dfrac{20x}{9-4x^2}}\) kifejezés. Határozzuk meg azon \(\displaystyle x\) egész számokat, amelyekre \(\displaystyle E(x)\) természetes szám.

Matlap (Kolozsvár)

(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2024. június 10-én LEJÁRT.

---

K/C. 817. Egy dobozban van négy papírcetli, amelyek mindegyikére egy-egy pozitív számot írtunk. Kihúzunk valahány cetlit, majd a rajtuk lévő számokat összeadjuk. (Ha egy cetlit húzunk ki, akkor azt a számot vesszük, amely a cetlin van.) Ezt az összes lehetséges módon megcsináljuk. Milyen számok vannak a cetlikre írva, ha az így kapott eredmények mind egymást követő egész számok?

(5 pont)

megoldás, statisztika

---

K/C. 818. Az \(\displaystyle ABC\) derékszögű háromszög befogóinak hossza \(\displaystyle BC=6\), \(\displaystyle CA=8\) egység. A \(\displaystyle BC\) befogó \(\displaystyle B\)-hez közelebb eső harmadolópontja \(\displaystyle P\), felezőpontja \(\displaystyle Q\), a \(\displaystyle CA\) befogó \(\displaystyle C\)-hez közelebbi harmadolópontja \(\displaystyle R\), felezőpontja \(\displaystyle S\), végül az \(\displaystyle AB\) átfogó \(\displaystyle A\)-hoz közelebbi harmadolópontja \(\displaystyle T\), felezőpontja \(\displaystyle U\). Tükrözzük a \(\displaystyle P\), \(\displaystyle R\), \(\displaystyle T\) harmadolópontokat az \(\displaystyle ABC\) háromszög hozzájuk legközelebb eső csúcspontjára, a \(\displaystyle Q\), \(\displaystyle S\), \(\displaystyle U\) felezőpontokat pedig a megfelelő háromszögoldal másik végpontjára az ábra szerint.

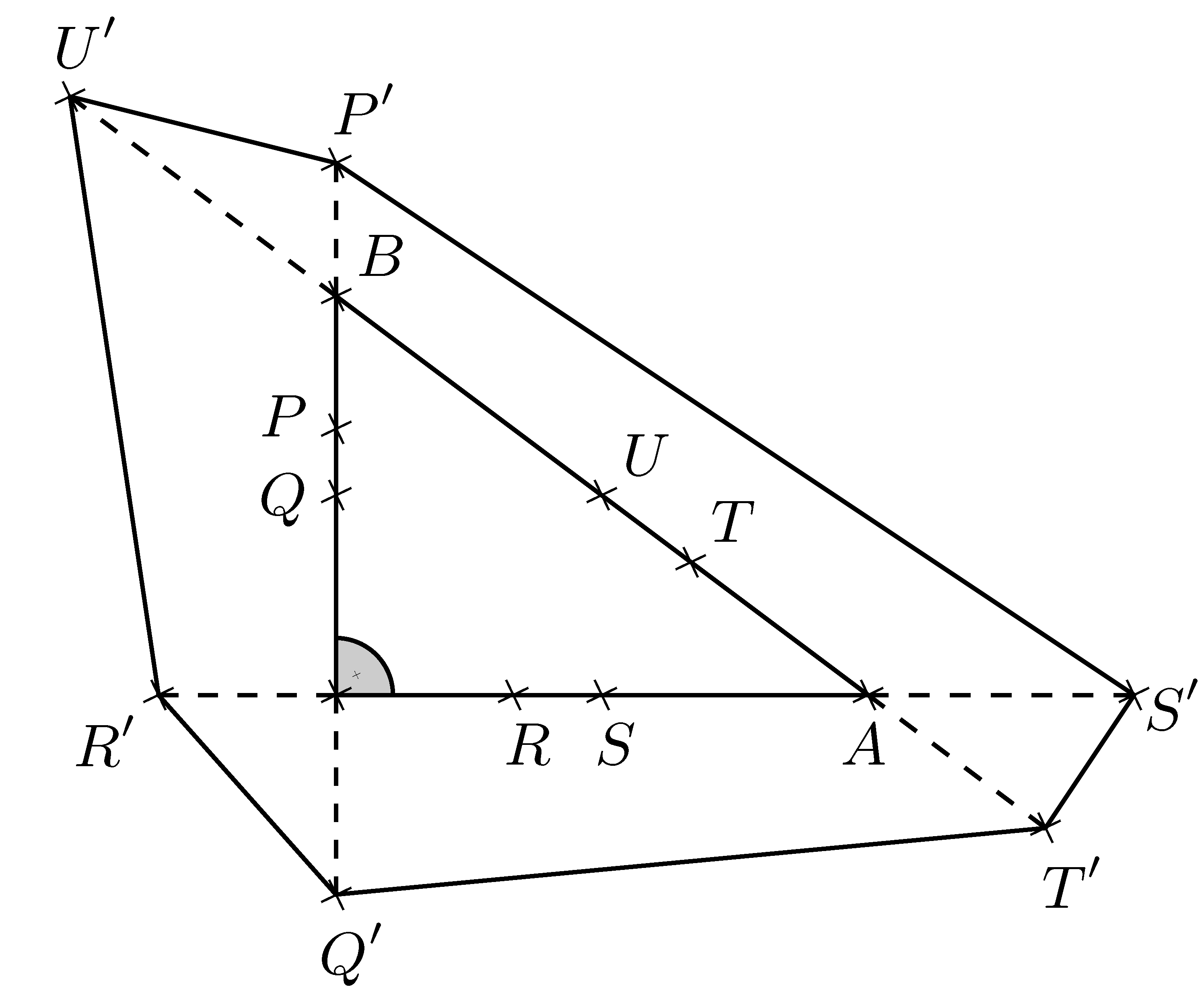
Határozzuk meg a \(\displaystyle P'U'R'Q'T'S'\) sokszög területét.

Javasolta: Bíró Bálint, (Eger)

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2024. június 10-én LEJÁRT.

---

C. 1813. Mutassuk meg, hogy nincsenek olyan \(\displaystyle m\), \(\displaystyle n\) pozitív egész számok, amelyekre

\(\displaystyle 3^{m}+3^{n}+1 \)

teljes négyzet.

amerikai versenyfeladat

(5 pont)

megoldás, statisztika

---

C. 1814. Milyen arányban osztja két részre az \(\displaystyle r\) sugarú kör területét az az egyenes, amelynek a kör középpontjától való távolsága \(\displaystyle \dfrac{r}{\sqrt{2}}\)?

Ringler András (Budapest)

(5 pont)

megoldás, statisztika

---

C. 1815. Oldjuk meg az

$$\begin{align*} x^2y-zu^2&=6,\\ x^2z+yu^2&=11 \end{align*}$$

egyenletrendszert, ha \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\), \(\displaystyle u\) természetes számok.

Katz Sándor (Bonyhád) ötlete alapján

(5 pont)

megoldás, statisztika

---

C. 1816. Az \(\displaystyle a=14\), \(\displaystyle b=13\), \(\displaystyle c=15\) hosszúságú oldalakkal rendelkező háromszög oldalai érintik az \(\displaystyle R=5\) sugarú gömböt. Határozzuk meg a gömb középpontja és a háromszög síkja közötti távolságot.

horvát versenyfeladat

(5 pont)

megoldás, statisztika

---

C. 1817. Elkezdtünk egy pénzérmét dobálni. A dobássorozat eredménye: egy fej, egy írás, egy fej, két írás, egy fej, három írás, egy fej és így tovább, azaz az írásokból álló megszakításmentes szériák hossza mindig 1-gyel növekszik, és azokat minden esetben egyetlen fej választja el egymástól. Ha ez a szabályosság megmarad, akkor hányadik dobás után hagyhatjuk abba a dobálást, hogy a fejek relatív gyakorisága pontosan \(\displaystyle \frac{1}{2023}\) legyen?

Barczy Mátyás, Nyul Gábor (Debrecen)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2024. június 10-én LEJÁRT.

---

B. 5390. Léteznek-e olyan \(\displaystyle a_0\), \(\displaystyle a_1\), \(\displaystyle \ldots\), \(\displaystyle a_{n-1}\) páros egész számok, amelyekre az \(\displaystyle x^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0\) polinom osztható az \(\displaystyle x^2+x+1\) polinommal?

Javasolta: Kós Géza (Budapest)

(3 pont)

megoldás, statisztika

---

B. 5391. Az egységnyi \(\displaystyle AB\) átmérőjű körvonalon kijelölünk egy \(\displaystyle C\) pontot. Ezután az \(\displaystyle AB\) szakaszon felvesszük a \(\displaystyle D\) és \(\displaystyle E\) pontokat úgy, hogy \(\displaystyle BD=BC\) és \(\displaystyle AE=AC\). Határozzuk meg \(\displaystyle AD^2+DE^2+EB^2\) lehetséges legkisebb értékét.

Javasolta: Szoldatics József (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5392. Tekintsünk egy olyan trapézt, amelynek területe egyenlő alapjainak szorzatával. Mutassuk meg, hogy ez a trapéz pontosan akkor érintőnégyszög, ha derékszögű.

Javasolta: Németh László (Fonyód)

(5 pont)

megoldás, statisztika

---

B. 5393. Legyen az \(\displaystyle f\) olyan valós-valós függvény, amelyre

\(\displaystyle \left|f(x+y+z)+\sin\,x+\sin\,y+\sin\,z \right|\le 3, \quad \text{minden } x, y, z\in \mathbb{R} \text{ esetén}. \)

Mutassuk meg, hogy \(\displaystyle |f(x)-\sin x|\le 1\) minden \(\displaystyle x\in \mathbb{R}\) esetén.

Javasolta: Bencze Mihály (Brassó)

(4 pont)

megoldás

---

B. 5394. Az \(\displaystyle ABCD\) négyzet középpontja \(\displaystyle O\), körülírt körének egy tetszőleges pontja \(\displaystyle X\). Jelölje \(\displaystyle T\) az \(\displaystyle X\) merőleges vetületét \(\displaystyle BC\)-n. Legyen az \(\displaystyle XB\) és \(\displaystyle AC\) egyenesek metszéspontja \(\displaystyle E\), az \(\displaystyle XC\) és \(\displaystyle BD\) egyeneseké pedig \(\displaystyle F\). Mutassuk meg, hogy \(\displaystyle EF\) merőleges \(\displaystyle TO\)-ra.

Javasolta: Vígh Viktor (Sándorfalva)

(4 pont)

megoldás, statisztika

---

B. 5395. Jelölje egy \(\displaystyle k\) pozitív egész pozitív osztóinak számát \(\displaystyle d(k)\), továbbá legyen \(\displaystyle 1<n\) egész szám. Melyik összeg a nagyobb, \(\displaystyle d(2)+d(4)+\dots+d(2n)\) vagy \(\displaystyle (d(1)+d(3)+\dots+d(2n-1))+(d(1)+d(2)+\dots+d(n))\)?

Javasolta: Pach Péter Pál (Budapest)

(5 pont)

megoldás, statisztika

---

B. 5396. Egy egyenlő oldalú térbeli (torz) ötszögnek négy derékszöge van. Mekkora lehet az ötödik szöge?

Javasolta: Dombi Péter (Pécs)

(6 pont)

megoldás

---

B. 5397. Egy gráfra (amely többszörös éleket is tartalmazhat) teljesül, hogy akárhogyan osztjuk szét a csúcsait \(\displaystyle t\) darab diszjunkt halmazba, legalább \(\displaystyle 2t-2\) él különböző halmazok között vezet. Bizonyítsuk be, hogy a gráf éleit ki lehet színezni pirosra vagy kékre úgy, hogy a kék és a piros élek is összefüggő (és minden csúcsot elérő) gráfot alkossanak.

Javasolta: Williams Kada (Cambridge, UK)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2024. június 10-én LEJÁRT.

---

A. 881. Egy királlyal bejárjuk egy (a szokásos módon színezett) \(\displaystyle n \times n\)-es sakktábla minden mezőjét pontosan egyszer. Határozzuk meg, hogy legkevesebb hányszor kellett színt váltanunk a séta során.

Javasolta: Pálvölgyi Dömötör (Budapest)

(7 pont)

megoldás, statisztika

---

A. 882. Legyen \(\displaystyle H_1\), \(\displaystyle H_2\), \(\displaystyle \ldots\), \(\displaystyle H_m\) a pozitív egész számok nemüres részhalmazai, legyen továbbá \(\displaystyle S\) ezen halmazok uniója. Bizonyítsuk be, hogy

\(\displaystyle \sum_{i=1}^m \sum_{a, b\in H_i} (a,b) \ge \frac{1}{m} \sum_{a, b\in S} (a, b), \)

ahol \(\displaystyle (a,b)\) az \(\displaystyle a\) és \(\displaystyle b\) legnagyobb közös osztóját jelöli.

(A \(\displaystyle \sum_{(a,b)\in X}\) azt jelöli, hogy a szumma az olyan \(\displaystyle (a, b)\) rendezett párokon fut végig, amikre \(\displaystyle a\in X\) és \(\displaystyle b\in X\).)

Javasolta: Matolcsi Dávid (Berkeley)

(7 pont)

megoldás, statisztika

---

A. 883. Legyenek \(\displaystyle J \subsetneq I \subseteq \mathbb{R}\) nemüres nyílt intervallumok, és legyenek \(\displaystyle f_1\), \(\displaystyle f_2\), \(\displaystyle \ldots\) olyan valós együtthatós polinomok, amelyekre a következők teljesülnek:

• \(\displaystyle f_i(x) \geq 0\) minden \(\displaystyle i \geq 1\) és \(\displaystyle x \in I\) esetén,
• \(\displaystyle \sum_{i=1}^\infty f_i(x)\) véges minden \(\displaystyle x \in I\) esetén,
• \(\displaystyle \sum_{i=1}^\infty f_i(x)=1\) minden \(\displaystyle x \in J\) esetén.

Következik-e ezekből, hogy \(\displaystyle \sum_{i=1}^\infty f_i(x)=1\) minden \(\displaystyle x \in I\) esetén is?

Javasolta: Imolay András (Budapest)

(7 pont)

megoldás, statisztika