|
| [1548] Fálesz Mihály | 2012-05-02 09:58:01 |
 Vannak speciális esetek, amikor egy sokadrendű görbe és egy kör metszéspontja véletlenül mégis szerkeszthető.
Jó lenne egy olyan esetet kipreparálni, amikor a megadott adatok "szépek", de az eredményben valami jól ismert, nem szerkeszthető mennyiség szerepel.
|
| Előzmény: [1547] BohnerGéza, 2012-05-02 02:11:52 |
|
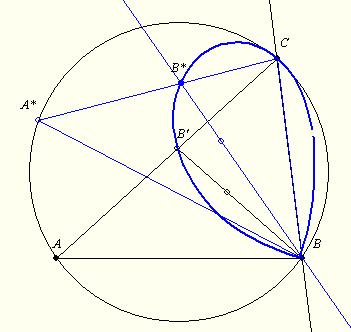
| [1547] BohnerGéza | 2012-05-02 02:11:52 |
 Egy példa, ahogyan a 178. feladat nem szerkeszthető:
(A BC oldal és a körülírt kör szerkeszthető.)
Tfh az ABC a szerkesztendő háromszög, ekkor a körülírt körén mozgó A* pont és a szerkesztőprogram segítségével kirajzolható az A*BC háromszög B* pontjainak nyomvonala. B* a B-ből induló szögfelező másik vége.
A B* nyomvonala nem másodrendű, így nem szerkeszthető.
A nyomvonal ismeretében B* számára meglenne a két szükséges vonal. (A másik a B kp-ú, az adott szögfelező sugarú kör.)
|
 |
| Előzmény: [1546] Konkoly Lászlóné, 2012-04-24 22:36:53 |
|
| [1546] Konkoly Lászlóné | 2012-04-24 22:36:53 |
 [1546] A 25. feladathoz hasonló szerkesztési feladat:
178.feladat: Szerkesszük meg a háromszöget (vagy mutassuk meg, hogy nem lehetséges), ha adott a háromszög egy oldala (a), a vele szemközti szög (alfa) és nem az alfához, mint a 25. feladatban, hanem egy másik szöghöz (pl. a bétá-hoz) tartozó szögfelező hossza.
|
|
| [1545] HoA | 2012-03-26 14:18:01 |
 "Úgy látom, leszoktunk a feladatok sorszámozása." (áról) Ne tegyük. A 174. volt szerintem az utolsó számozott. Legyen [1531] a 175. , [1537] a 176. és most jöjjön a
177. feladat: Az ABCD húrnégyszög csúcsai által meghatározott ABC, BCD, CDA, DAB háromszögek beírt köreinek középpontja legyen OD , OA , OB , OC . A CD oldalegyenest messe ODOA E-ben, OCOB F-ben . Bizonyítsuk be, hogy ABEF húrnégyszög.
|
| Előzmény: [1531] BohnerGéza, 2011-12-31 01:11:20 |
|
| [1542] Danesz | 2012-03-19 19:18:17 |
 Ja, a kötözködők kedvéért: A definícióban nincs szó síklapokról :P
|
|
| [1541] Danesz | 2012-03-19 19:12:04 |
 A tér a 3-dimenziós euklideszi tér. Ismétlem a definíciót kicsit másképpen: Az A halmaz átdarabolható a B halmazba, ha Az A halmaz felbontható véges sok olyan A1, A2, ..., An diszjunkt halmazra (vagyis az Ai halmazok uniói kiadják A-t), hogy ezeket az Ai halmazokat valamilyen (lehet, hogy minden i-re különböző) mozgással átvihetünk olyan Bi (természetesen szintén n darab) diszjunkt halmazba, hogy a Bi-k egyesítése kiadja B-t. Remélem elég részletes és pontos. Ja, és a mozgás az irányítástartó izometria (legjobb tudásom szerint)
|
| Előzmény: [1540] Fálesz Mihály, 2012-03-18 13:13:44 |
|
| [1540] Fálesz Mihály | 2012-03-18 13:13:44 |
 Nem egyértelmű, hogy mi a kérdés. Mit nevezel "átdarabolás relációnak"? Mi a "tér"? Hány darabra vághatunk? Csak véges sokra, vagy megszámlálható sokra? Csak síklapokkal vághatunk, vagy diszjunkt részhalmazokra bontunk?
Végtelen sok diszjunkt darab megengedése esetén elismételheted a Cantor-Bernstein-Schröder tétel valamelyik bizonyítását.
|
| Előzmény: [1536] Danesz, 2012-03-17 18:42:39 |
|
| [1539] Fálesz Mihály | 2012-03-18 13:05:06 |
 Az egy egyenesen levő szakaszok arányai között több összefüggést találhatsz akár közvetlenül, akár a Menelaosz-tétel felírásával.
Az ADC, BEC, APE, BPD egyeneseken a különböző szakaszok arányát kifejezheted a területekkel, például  . .
Ezekből összerakhatod a megoldást...
|
| Előzmény: [1537] Sudárné, 2012-03-18 09:32:48 |
|
|
| [1537] Sudárné | 2012-03-18 09:32:48 |
 A feladat a következő: Egy háromszög egy-egy oldalán vegyünk fel egy-egy tetszőleges pontot (jelöljük mondjuk D-vel és E-vel) Ezeket a pontokat kössük össze a velük szemközt lévő háromszög csúcsával. A háromszög így négy részre bomlott, három háromszögre és egy négyszögre, A három háromszög területét ismerem, kérdés a négyszög területe.
Az ábrán találhatóak a további adatok.
|
 |
|
| [1536] Danesz | 2012-03-17 18:42:39 |
 Üdv mindenkinek! Segítenétek egy feladat kidolgozásában? Bizonyítandó, hogy a tér részhalmazain értelmezett átdarabolás relációra igaz, hogy ha A átdarabolható B egy részhalmazába, és B átdarabolható A egy részhalmazába, akkor A átdarabolható B-be. (A átdarabolható B-be, ha létezik az A=U(A(i)) véges diszjunkt felbontás és B=U(B(i)) véges diszjunkt felbontás, hogy A(i) mozgással átvihető B(i)-be)
[U az unió jele]
|
|
|
|
| [1533] BohnerGéza | 2012-01-11 00:58:59 |
 Mint HoA megoldásából is látszik, ha P közelebb van a vezéregyeneshez mint a fókuszpont, de P nincs a tengelyen, akkor is igaz az 1531-beli állítás. Ekkor a nagyítás aránya negatív.
|
| Előzmény: [1532] HoA, 2012-01-08 16:41:15 |
|
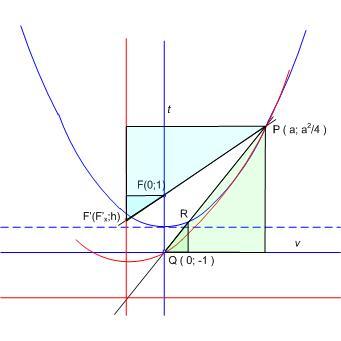
| [1532] HoA | 2012-01-08 16:41:15 |
 Nem nagy a tolongás. Egy mechanikus bizonyítás, mely talán kedvet vagy ötletet ad egy szemléletesebbhez: Válasszuk úgy a koordinátarendszer egységét, hogy a parabola egyenlete  legyen. Ekkor F koordinátái ( 0;1) , v és t metszéspontja Q( 0;-1) . Legyen legyen. Ekkor F koordinátái ( 0;1) , v és t metszéspontja Q( 0;-1) . Legyen  , ahol a feltétel szerint a>2 . A PQ egyenes és a parabola második metszéspontjára ( R ) felírt, x-re adódó másodfokú egyenletből (x-a) kiemelhető, a másik megoldás , ahol a feltétel szerint a>2 . A PQ egyenes és a parabola második metszéspontjára ( R ) felírt, x-re adódó másodfokú egyenletből (x-a) kiemelhető, a másik megoldás  . A nagyítás során R képe Q, F képe F' ,ennek ordinátája legyen h. A lineáris méretek azonos nyújtása miatt a zöld illetve kék hasonló háromszögek hasonlósági aránya megegyezik: . A nagyítás során R képe Q, F képe F' ,ennek ordinátája legyen h. A lineáris méretek azonos nyújtása miatt a zöld illetve kék hasonló háromszögek hasonlósági aránya megegyezik:  ; ;  ; ;  , ebből pedig a > 2 miatt h=0 . , ebből pedig a > 2 miatt h=0 .
|
 |
| Előzmény: [1531] BohnerGéza, 2011-12-31 01:11:20 |
|
| [1531] BohnerGéza | 2011-12-31 01:11:20 |
 jonas [1530]: Azért ne ijesszük el az olvasókat. Megy egyszerűbben is! HoA leírásából nem következik?
(Úgy látom, leszoktunk a feladatok sorszámozása.) Egy másik feladat:
|
 |
|
|
|
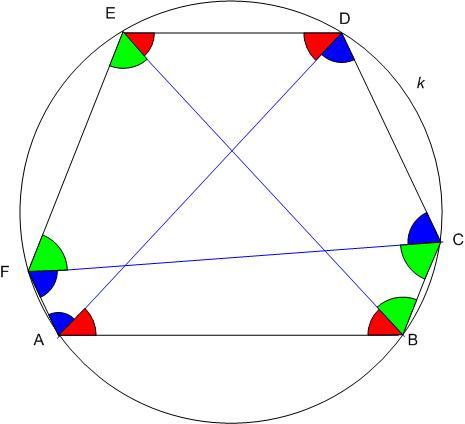
| [1528] HoA | 2011-12-24 09:45:55 |
 Elnézést, figyelmetlen voltam. Természetesen nem igaz, hogy az átlók felezik egymást. ( Ld. ábra ) . Egy megoldás: Addig igaz, hogy AB és DE párhuzamosságából valamint AD és BE egyenlő hosszából adódik, hogy a két átló egyenlő szögeket zár be a párhuzamos oldalakkal. Az ábrán pirossal jelölt szögek ABE  = BAD = BAD  = DEB = DEB  = EDA = EDA  , legyen , legyen  . Hasonlóan CDA . Hasonlóan CDA  = FCD = FCD  = DAF = DAF  = CFA = CFA  , legyen , legyen  ( kék ), valamint CBE ( kék ), valamint CBE  = BCF = BCF  = BEF = BEF  = CFE = CFE  , legyen , legyen  ( zöld ). BAD ( zöld ). BAD  = DEB = DEB  miatt ABDE húrnégyszög, körülírt köre legyen k. A hatszög szögeinek összegére 720o = 4 miatt ABDE húrnégyszög, körülírt köre legyen k. A hatszög szögeinek összegére 720o = 4  + 4 + 4  + 4 + 4  , így , így  + +  + +  = 180o . k -ban a BD húrhoz tartozó egyik kerületi szög = 180o . k -ban a BD húrhoz tartozó egyik kerületi szög  , BCD , BCD  = =  + +  , így ABCD húrnégyszög, C is rajta van k -n. Ugyanígy adódik, hogy F is rajta van k -n. , így ABCD húrnégyszög, C is rajta van k -n. Ugyanígy adódik, hogy F is rajta van k -n.
|
 |
| Előzmény: [1526] logarlécész, 2011-12-22 19:00:43 |
|
|
| [1526] logarlécész | 2011-12-22 19:00:43 |
 Szerintem nem feltétlenül felezik egymást a szakaszok (nem a feladat végén, hanem abból, hogy egyenlő hosszúak), én legalábbis nem látom, hogy ez honnan jött.
Viszont azt hiszem, az biztos, hogy ha a hat csúcsból két szemköztit elhagyunk, a maradék húrnégyszöget alkot (egyenlő átlójú trapéz), de ebből következik a megoldás?
|
| Előzmény: [1522] HoA, 2011-12-20 17:31:48 |
|
|
|
|
| [1522] HoA | 2011-12-20 17:31:48 |
 Vázlat: Javaslom a párhuzamos szelők - egyik - tételének egy "megfordítását" : párhuzamosok közötti párhuzamos szakaszok egyenlőek --> párhuzamosok közötti egyenlő szakaszok vagy párhuzamosak vagy ugyanakkora szöget zárnak be a párhuzamosakkal. Ebből adódik, hogy az átlók felezik egymást, és mivel egyenlőek a hat csúcs az átlók metszéspontjától félátlónyi távolságra van, tehát egy körön vannak.
|
| Előzmény: [1521] Erika95, 2011-12-20 17:01:06 |
|
| [1521] Erika95 | 2011-12-20 17:01:06 |
 Sziasztok! A segítségeteket szeretném kérni az alábbi feladat megoldásában: Bizonyítsuk be,hogy egy hatszög szemben fekvő oldalai párhuzamosak és a szembenfekvő csúcsokat összekötő átlók egyenlőek egymással, akkor a hatszög csúcsai egy körön vannak. A hatszög nem biztos hogy szabályos hatszög.
Köszönöm szépen.
|
|
|
|
| [1518] Tatanka Yotanka | 2011-12-12 10:05:37 |
 Kedves Sirpi! Kérdésed, hogy "miért a szögfelezőkre?" teljesen jogos. A DEF háromszög (és a hasonló eljárással létrehozott GHI, JKL háromszögek is) mindig hasonló az ABC háromszöghöz, nem kell, hogy a B,C pontokból az A-ból szögfelezőre bocsássunk merőlegest, elegendő egy A-ból induló, és a szemközti oldalt metsző egyenes, sőt, akár a szemközti oldallal párhuzamos is lehet. A szögfelezős változat nyilván egyszerűbb, a hasonlóság arányát könnyebb fölírni.
|
|
| [1517] Tatanka Yotanka | 2011-12-12 09:09:58 |
 Bocsánat, egy feltételt kihagytam a fölvetett feladatból. Az A pontbeli belső szögfelezőre a B és C pontokból bocsátunk merőlegest. Hiába, kezdő vagyok.
|
|
|
| [1515] Tatanka Yotanka | 2011-12-12 07:00:59 |
 Üdvözlet mindenkinek! Új hozzászólóként szeretnék egy feladatot, illetve problémát fölvetni: Az ABC háromszög A csúcsából bocsássunk merőlegest a szemben levő oldalra, a merőleges talppontja legyen D. Ezután állítsunk merőlegeseket az A-ból induló belső szögfelezőkre, a talppontok itt E és F. Hasonlóképpen szerkesztjük meg a C és B pontokból kiindulva a GHI és JKL háromszögeket. Az könnyen igazolható, hogy DEF, GHI és JKL mindegyike hasonló az ABC háromszöghöz, de ezen háromszögek területének összege lehet-e pl. az ABC háromszög területével egyenlő, annak a fele stb., illetve mennyi a három terület összegének maximuma?
|
|
| [1514] Lajos bácsi | 2011-12-09 18:04:34 |
 Na végre, azt hittem nem lesznek válaszok, de úgy látom, nem sok ember képzelőerejét mozgatta meg a felvetett kérdés.
|
|
|
|
| [1511] Lajos bácsi | 2011-12-07 15:03:45 |
 Rajzoljátok vagy írjátok le azt a 3 dimenziós tárgyat, melyet különbözőképpen elforgatva és megvilágítva az ábrán látható árnyképeket produkálná.
|
 |
|
| [1510] Vonka Vilmos Úr | 2011-06-18 18:18:56 |
 Következzen inkább csak egy kis útmutatás, remélem, utána könnyebb lesz megoldanod a feladatot.
1. Legyen a szabályos n-szög középpontja O, két szomszédos csúcsa A és B. A szabályos n-szög helyett vizsgáljuk az ABO egyenlő szárú háromszöget. Ebben a háromszögben milyen adat R és milyen adat r? Ha ezt meggondoltad, akkor legyen F az AB szakasz felezőpontja, és vizsgáljuk (például) az AFO háromszöget. Ez a háromszög derékszögű (miért?), így bármelyik oldalát könnyedén kiszámíthatjuk szögfüggvények segítségével. Ha már látod, hogy az ABO háromszög milyen adatai R és r, akkor ennek a háromszögnek az oldalhosszai elvezetnek a R-re és r-re vonatkozó formulákhoz.
A terület kiszámításához is elég az ABO háromszög területét meghatároznod. (Hányszorosa ennek a szabályos n-szög területe?)
2. Az előző formulákba n=8-at kell behelyettesíteni. Ehhez pi/8 szögfüggvényeinek pontos értékére van szükséged. Ez egy nevezetes szög (45 fok) fele, ezért a félszögek szögfüggvényeire vonatkozó képletek (nézz utána!) alapján kaphatod meg a szükséges formulákat.
3. Itt szintén az 1. feladatban nyert képletekbe kell behelyettesíteni. A szögfüggvények pontos értékei csak n=5 és n=10 esetén nem annyira ismertek. Ezek közül nyilván elég az egyiket kiszámítani. (A másik a kétszeres szögre vagy félszögre vonatkozó képletek alapján adódik.) n=10 esetén például a 18 fokos szög szögfüggvényeire lesz szükség. Az erre vonatkozó számításokhoz segítség: annak az egyenlő szárú háromszögnek, amelynek alapon nyugvó szögei 72 fokosak, az alapja és a szára az aranymetszés szerint aránylik egymáshoz, azaz arányuk (gyök(5)-1)/2.
|
| Előzmény: [1509] virágzótisza, 2011-06-18 14:50:10 |
|
| [1508] Maga Péter | 2011-06-18 17:28:48 |
 Innen ilyenekért nem fognak kitiltani (feltéve, hogy nem valamely aktív KöMaL-feladathoz kapcsolódik a kérdésed:)), tudunk ,,ilyesmiről'' beszélgetni.
A feladatokat nem lövöm le. Nem tudom, hogy van-e egyáltalán olyan látogatója a fórumnak, aki még életében nem gondolta meg az ismertetett formulákat...
Javaslom az oldalon található TeX tanfolyam elvégzését, már ezeket a bevezető képleteket is kellemetlen ebben a formában olvasni.
|
| Előzmény: [1509] virágzótisza, 2011-06-18 14:50:10 |
|
| [1509] virágzótisza | 2011-06-18 14:50:10 |
 Sziasztok! Ahányszor csak kérdezek, vagy nicket regisztrálok az index fórumon, annyiszor kitörlik kérdésemet és kitiltanak. Most a matematika-elsősegély topikból tiltottak ki az alábbi kérdések miatt.
1. Bizonyítsuk be, hogy az a oldalhosszúságú szabályos n szög köré írt kör sugara R=a/(2sin(pi/n)), beírt kör sugara r=a/2tg(pi/n) terülte S=nar/2 2. Mutassuk meg 1. felhasználásával, hogy a szabályos nyolcszögre R=agyök(1+(gyök2)/2), r=a(1+gyök(2))/2, S=2a**2(1+gyök(2)) 3. Töltse ki az alábbi táblázatot: n, R,r,S, ahol n =3,4,5,6,10 (A fenti alakhoz hasonlóan adja meg a formulákat!)
Tudunk itt ilyesmiről beszélgetni?
|
|
|
|
|
|
|
|
| [1501] gubanc | 2011-04-19 12:03:38 |
 A 2)-höz: Így egyszerűbb volt a számítás, mert meg lehetett spórolni a 4R-es szorzó többszöri leírását.
Köszönöm a részletes "helyretételt". A dorgálást megérdemlem, hiszen egy félreértés miatt árnyékra vetődtem és előbb írtam, mint gondolkoztam. Több tanulság van, az egyik, hogy késő éjszaka, hullafáradtan nem szabad matekoznom ... .
Nem állt szándékomban megbántani, főleg nem Téged, hiszen korábban és most is nagy élvezettel olvastam, olvasom frappáns levezetéseidet, megoldásaidat. Elnézést, ha megbántottalak volna. Üdv: gubanc
|
| Előzmény: [1500] nadorp, 2011-04-19 10:34:47 |
|
| [1500] nadorp | 2011-04-19 10:34:47 |
 Az "álbizonyítás" megjegyzésed kissé erős...De ettől függetlenül:
1). Idézet tőlem: "nálam minden x,y,z távolságra van megoldás ( az más kérdés, hogy ez szerkeszthető-e)"
Ezzel azt a félrértést szeretném eloszlatni, hogy én csak a megoldhatóságot ( diszkussziót ) vizsgáltam, nem a geometriai szerkeszthőséget.
2.) Az eredeti feladat szerint: Szerkesszük meg a háromszöget, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai.
Nem értem, minek kell feltenni, hogy R=1/4. Adott három független adat, szerkesszük meg a háromszöget ( felejtsd most el a hasonlóságot)
3.) "A (*) tartományon kívül eső szögek nem adnak megoldást."
Ez értelmetlen, mert a (*) tartományba nem szögek, hanem szakaszok hosszai esnek.
4.)"A leírtak következménye: az általad előállított f függvény a t = 0 helyen nincs értelmezve, hiszen 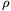 > 0 egyben > 0 egyben  > 0-t is jelenti" > 0-t is jelenti"
Már dehogy nincs értelmezve a t=0 és t=1 helyen, félreértésben vagy. Az, hogy megoldásként csak 0 és 1 közti megoldást fogadunk el, attól még a függvény értelmezve van a végpontokban és a Bolzano-tétel is használható rá. ( Így keletkeznek a "Híres álcáfolatok" ).
Fordítva gondolkozzál, a Bolzano-tétel csak egy eszköz. Az egyenletrendszer megoldásából adódik, hogy ha ennek a függvénynek van (0;1)-beli zéróhelye, akkor az megadja  értékét. A Bolzano-tétel ( vagy általában az, hogy zárt intervallumon folytonos függvény tetszőleges két felvett értéke közti értéket is felvesz) csak biztosítja a gyök létezését. A 0 sugarú körrel való "bűvészkedés" helyett pedig tekintsd az f függvényt az [ értékét. A Bolzano-tétel ( vagy általában az, hogy zárt intervallumon folytonos függvény tetszőleges két felvett értéke közti értéket is felvesz) csak biztosítja a gyök létezését. A 0 sugarú körrel való "bűvészkedés" helyett pedig tekintsd az f függvényt az [ ;1- ;1- ] intervallumon, ahol ] intervallumon, ahol  olyan kicsi pozitív szám, hogy f( olyan kicsi pozitív szám, hogy f( )<0 és f(1- )<0 és f(1- )>0 és egyből megszűnnek az értelmezésbel gondjaid. )>0 és egyből megszűnnek az értelmezésbel gondjaid.
5.) "Egyébként jó, hogy ez a probléma is felmerült, mert roppant tanulságosnak tartom"
Akkor tanulj belőle.
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1499] Kemény Legény | 2011-04-19 10:11:38 |
 "Azt mondod, hogy ha egy racionális együtthatós harmadfokú egyenletnek nincs racionális gyöke, akkor a gyökei nem szerkeszthetőek?"
Igen.
Arra, hogy egy szám nem szerkeszthető, elégséges feltételt ad az, hogy a minimálpolinomjának a foka nem kettőhatvány. Márpedig azok a rac. együtthatós harmadfokú polinomok, amiknek nincs rac. gyökük, irreducibilisek.
|
| Előzmény: [1498] jonas, 2011-04-19 10:02:13 |
|
| [1498] jonas | 2011-04-19 10:02:13 |
 Hogy van ez? Azt mondod, hogy ha egy racionális együtthatós harmadfokú egyenletnek nincs racionális gyöke, akkor a gyökei nem szerkeszthetőek? Ez miért olyan triviális? Negyedfokú egyenletre mondjuk biztos nem lenne igaz, mert mondjuk két általános racionális együtthatós másodfokú polinom szorzata egy olyan racionális együtthatós negyedfokú polinom, aminek nincs racionális gyöke, de minden gyöke szerkeszthető.
|
| Előzmény: [1497] Kemény Legény, 2011-04-19 07:59:51 |
|
| [1497] Kemény Legény | 2011-04-19 07:59:51 |
 Attól most tekintsünk el, hogy mennyire érted/nem érted a Bolzano-tétel használatát (az ember nem szívesen ért egyet Róbert Gidával, de ha egyszer igaza van...), térjünk inkább vissza az euklideszi szerkeszthetőség vizsgálatára. (Mellesleg gyanítom, itt még több olyan rész fog következni, amikkel esetleg gondok lehetnek...)
Állítás: nincs általános módszer, amivel tetszőlegesen adott x,y,z esetén megszerkesztenéd (a szokásos euklideszi szerkesztésekkel) a háromszögedet.
Bizonyítás: A nadorp által levezetett egyenletből kapjuk a harmadfokú 2x2yzt3+(x2y2+y2z2+z2x2)t2-y2z2=0 egyenletet. Ez az egyenlet például az x=1<y=2<z=3 választás esetén a 12t3+49t2-36=0 alakot ölti. A bal oldalon álló egész együtthatós polinomnak nincs racionális gyöke (ha nem ismernéd ennek az eldöntésére szolgáló módszert, kérdezz meg egy Maple, Mathematica, stb. jellegű szoftvert vagy olvasd el itt). Tehát a harmadfokú polinom irreducibilis, a kiindulási adataink: (x,y,z)=(1,2,3) egészek voltak, innen a szerkeszthetőségről szóló Galois-elmélet egyszerű következményeként nem szerkeszthető meg  , ami ekvivalens a háromszög szerkesztésének lehetetlenségével. (gondold végig...) , ami ekvivalens a háromszög szerkesztésének lehetetlenségével. (gondold végig...)
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1496] Róbert Gida | 2011-04-19 02:56:20 |
 nadorp szerintem hallott már a Bolzano tételről... Amúgy miért baj, a nulla sugarú kör? Formálisan miért nem nézhetnéd az egyenletet? [t egy változó] A megoldás (0,1)-beli, azaz nem lesz nulla sugarú kör a megoldás. Ugyanez van a másik oldalon.
Amúgy ezeknek a klasszikus tételeknek vannak javított változatai. Amikor nyílton folytonos és egyoldali limesz van a végpontokban stb.
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1495] gubanc | 2011-04-19 02:13:48 |
 Szia nadorp!
A folytonos függvényekre vonatkozó Bolzano tételt próbáltad alkalmazni, amely így szól:
Ha a g függvény az [a, b] zárt intervallumon folytonos és g(a), g(b) különböző előjelűek, akkor az intervallumban van olyan c pont, amelyre g(c) = 0.
0 sugarú beírt kör nem értelmezhető, így fennáll, hogy 0 <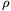 < x és z < x és z  , ahol a háromszög köré írt kör sugara: , ahol a háromszög köré írt kör sugara:  . A távolságokra megadott egyenlőtlenséglánc tehát így teljes: . A távolságokra megadott egyenlőtlenséglánc tehát így teljes:  . (*) . (*)
A leírtak következménye: az általad előállított f függvény a t = 0 helyen nincs értelmezve, hiszen 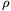 > 0 egyben > 0 egyben  > 0-t is jelenti. A másik végponttal is baj van, hiszen a > 0-t is jelenti. A másik végponttal is baj van, hiszen a  egyenlőségből következne, hogy egyenlőségből következne, hogy  =180°, ami egy háromszöben szintén lehetetlen. Az f függvény tehát nem tesz eleget a Bolzano tétel feltételeinek, így a tétel itt nem alkalmazható. Ezzel megcáfoltuk az állításod, mely szerint „ nálam minden x, y, z távolságra van megoldás”. =180°, ami egy háromszöben szintén lehetetlen. Az f függvény tehát nem tesz eleget a Bolzano tétel feltételeinek, így a tétel itt nem alkalmazható. Ezzel megcáfoltuk az állításod, mely szerint „ nálam minden x, y, z távolságra van megoldás”.
A (*) tartományon kívül eső  szögek nem adnak megoldást. szögek nem adnak megoldást.
(Egyébként jó, hogy ez a probléma is felmerült, mert roppant tanulságosnak tartom. Akár a "Híres(?) álbizonyítások" témába is át lehetne másolni ...)
E kis kitérő után visszatérhetünk az euklidészi szerkeszthetőség vizsgálatára.
|
| Előzmény: [1494] nadorp, 2011-04-17 10:32:14 |
|
| [1494] nadorp | 2011-04-17 10:32:14 |
 Nem tudom, mit számoltam el, de nálam minden x,y,z távolságra van megoldás ( az más kérdés, hogy ez szerkeszthető-e). Vázlatosan:
Tegyük fel, hogy x y y z. Ekkor z. Ekkor
 , ahol , ahol 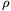 a beírt kör sugara. a beírt kör sugara.



Négyzetre emeléssel és rendezéssel valóban egy harmadfokú egyenletet kapunk  -re, de most nem ez a lényeg, hanem -re, de most nem ez a lényeg, hanem
 jelöléssel a bal oldalon egy olyan, a [0,1] intervallumon mindenhol értelmezett ( felhasználtuk, hogy y jelöléssel a bal oldalon egy olyan, a [0,1] intervallumon mindenhol értelmezett ( felhasználtuk, hogy y x ), folytonos f(t) függvény áll, amelyre x ), folytonos f(t) függvény áll, amelyre
f(0)=-zy<0 és f(1)=xz+xy>0, tehát létezik zéróhelye a (0,1) intervallumon. Hol a hiba? Nem látom, hogy az így kapott  szög mikor nem ad megoldást? szög mikor nem ad megoldást?
|
| Előzmény: [1493] gubanc, 2011-04-16 21:06:36 |
|
| [1493] gubanc | 2011-04-16 21:06:36 |
 Legyenek az 1/4 sugarú körbe írt ABC háromszög szögei  , ,  , ,  . A beírt kör középpontjának az A, B, C csúcsoktól mért távolságai x, y, z. Ezeket kaptam (a részleteket most mellőzöm): . A beírt kör középpontjának az A, B, C csúcsoktól mért távolságai x, y, z. Ezeket kaptam (a részleteket most mellőzöm):  , ,  , ,  . .
Ezekből kiindulva egyelőre nem tudom kihozni, hogy mely ( , , ) szögpárra szerkeszthető meg az x, y, z távolságokból egy háromszög. Csak a korábban említett halvány "gyanú" merült fel bennem. ) szögpárra szerkeszthető meg az x, y, z távolságokból egy háromszög. Csak a korábban említett halvány "gyanú" merült fel bennem.
A Te harmadfokú egyenleted viszont biztatónak tűnik. Esetleg fel tudnád tenni?
|
| Előzmény: [1492] Maga Péter, 2011-04-14 19:56:58 |
|
| [1492] Maga Péter | 2011-04-14 19:56:58 |
 Én egy harmadfokú egyenletet kaptam. Abból a szerkeszthetőség kérdése (konkrétan megadott kezdeti adatokból) mindig könnyen eldönthető. Az nem világos nekem, hogy a tartományt hogyan lehetne egyszerűen leírni, bár nem is nagyon gondolkodtam rajta. Lehet, hogy nem nehéz, de az is lehet, hogy ennél lényegesen egyszerűbb leírást nem is lehet adni.
|
| Előzmény: [1491] gubanc, 2011-04-14 16:47:40 |
|
| [1491] gubanc | 2011-04-14 16:47:40 |
 Köszönöm, hogy végigszámoltad. Én is ilyen következtetésre jutottam. Ha jól értem, ez azt jelenti, hogy 1-ből hiányzik a szerkeszthető háromszögeket megadó értelmezési tartomány. Ezzel el is jutottunk 2-höz.
|
| Előzmény: [1490] Maga Péter, 2011-04-13 16:24:00 |
|
|
| [1489] gubanc | 2011-04-13 14:41:02 |
 Sziasztok!
Kigondoltam egy feladatot, de nem jövök rá, hogyan kellene hozzáfogni és megoldani. Íme:
1. Szerkesszük meg a háromszöget, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai.
És/vagy:
2. Melyek azok a háromszögek, amelyek megszerkeszthetők, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai?
A 2.-nál arra gyanakszom, hogy a keresett háromszögek szögei a nevezetes szögekből származtathatók … (Ha mégsem, vagy nem jók a feladatok, bocsi előre is.)
Köszönettel: gubanc
(Sok van, mi csodálatos, de a Geometriánál nincs semmi csodálatosabb! :)
|
|
|
| [1487] HoA | 2011-04-11 14:41:37 |
 Komolyra fordítva: Legyen k1 és k2 két egymást metsző kör, metszéspontjaik C és D. k2 kör k1-en kívül eső CD ívén vegyünk fel egy P pontot. A PD és PC egyenesek k1-gyel alkotott második metszéspontja legyen A illetve B . Bizonyítsuk be, hogy az AB=a szakasz hossza független P választásától.
Előkészítésül tekintsünk egy ABCD húrnégyszöget, ahol AB=a>CD=c . A BC és AD egyenesek metszéspontja legyen P . ABCD körülírt körében legyenek az oldalakhoz mint húrokhoz tartozó kerületi szögek  , , , , , , . Ekkor ABCD szögeinek összege 2.( . Ekkor ABCD szögeinek összege 2.( + + + + + + )=360o , tehát )=360o , tehát  + + + + + + =180o . A BPA szöget =180o . A BPA szöget 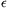 -nal jelölve az ABP háromszögben -nal jelölve az ABP háromszögben  +2 +2 + + + +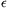 =180o= =180o= + + + + + + , ahonnan , ahonnan 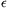 = = - -
Feladatunkra alkalmazva az eredményt, a mi ABCD húrnégyszögünkben CD=c rögzített, így  állandó, BPA állandó, BPA = =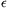 =CPD =CPD állandó, mint k2-ben a CD húrhoz tartozó kerületi szög, ezért állandó, mint k2-ben a CD húrhoz tartozó kerületi szög, ezért  = =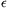 + + is állandó, vagyis k1 -ben az AB húrhoz tartozó kerületi szög és így AB=a hossza is független P helyzetétől. is állandó, vagyis k1 -ben az AB húrhoz tartozó kerületi szög és így AB=a hossza is független P helyzetétől.
|
 |
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1486] HoA | 2011-04-11 08:17:58 |
 Mi az, ami adott? Például: adott két egymást metsző, egyébként tetszőleges kör ... Ahogy a kérdést feltetted, biztosan nem igaz az állítás: Ha kétszer akkora ábrát rajzolok, az a szakasz is kétszer akkora lesz - akármelyik is legyen az ábrán az a szakasz - mert én azt sem látom, melyik az.
|
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1485] eperke | 2011-04-10 17:17:34 |
 Ez így jó lesz?Nagyobbra nem megy..:S
|
 |
|
| [1484] jonas | 2011-04-10 16:21:47 |
 A 80-szor 100 pixel méret az avatarra vonatkozik, ami minden hozzászólásod mellett megjelenik. A csatolt ábra lehet nagyobb is, bár az sem lehet túl nagy.
|
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1483] Radián | 2011-04-10 16:10:05 |
 Hello!
Nem tudnál egy nagyobb képet bevágni, vagy linket küldeni ahol nagyobb méretben, jó felbontásban láthatjuk az ábrát, mert (legalábbis én) így nem tudok segíteni.
|
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1482] eperke | 2011-04-10 15:38:14 |
 Hali.Egy kis segítségre lenne szükségem. Azt kell belátni , hogy az a szakasz mindig ugyanolyan hosszú.
|
 |
|
| [1481] Füge | 2011-01-19 18:49:05 |
 Jajj elnézést az utolsót visszavonom elnéztem a kettest :)
|
|
| [1480] Füge | 2011-01-19 18:47:45 |
 Ja és igen a megadott képleted is hibás, ugyanis
 tehát tehát 
|
|
| [1479] Füge | 2011-01-19 18:36:42 |
 Arra gondoltam, hogy melyik az a legszűkebb intervallum, amelybe mindenképp beleesik az  hányados. hányados.
|
|
| [1478] Radián | 2011-01-19 18:23:11 |
 Gyanítom, hogy félreértettem a feladatod de talán a hibás eredményemből majd kiderül mire is gondoltál. Szerintem: r/m=(a+b-c)c/2ab ahol r a beírt kör sugara, m az átfogóhoz tartozó magasság hossza míg a két befogót a ill b-vel az átfogót pedig c-vel jelöltem. Igazából nem értem, hogy ezt miért becsülni kell s nem kiszámolni...
|
| Előzmény: [1477] Füge, 2011-01-19 15:01:45 |
|
| [1477] Füge | 2011-01-19 15:01:45 |
 Egy könnyebb feladat, de nekem tetszett.
174.feladat: Egy tetszőleges derékszögű háromszögben adjuk minél jobb közelítést a beírt kör sugarának és az átfogóhoz tartozó magasságnak a hányadosára.
|
|
| [1476] HoA | 2011-01-07 21:52:17 |
 Ha a P ponton átmenő, sugárra merőleges húr hossza 2a, egy másik húrt a P pont b és c hosszúságú szakaszokra oszt, akkor a szelőtételből
a2=b.c
és a számtani - mértani közép tételből

|
| Előzmény: [1465] Nánási József, 2010-12-30 22:47:46 |
|
|
| [1474] BohnerGéza | 2011-01-03 13:45:49 |
 173. feladat: Adott két kör és egy pont. Szerkesztendő az a középpontos hasonlóság, melynek középpontja az adott pont és melynél az egyik kör képe érinti a másik adott kört.
|
|
|
| [1472] Füge | 2011-01-02 14:08:50 |
 Én deriváltam a parabola egyenletét (mert y=ax2+bx+c alakú volt), és azt tettem egyenlővé a kapott meredekséggel, onnan számoltam pontot, majd m(x-x0)=y-y0 A feladat többi részével nem volt gond, csak azon filóztam, hogy kell-e bizonyítás, vagy sem :)
|
|
| [1471] lorantfy | 2011-01-02 13:37:38 |
 Szerintem itt nem kell a bizonyítással vacakolni. Ezt ismertnem vesszük. Felteszem, hogy a P pont az O középpontú körön belül van:
1. Felirjuk P ponton átmenő OP normálvektorú egyenes egyenletét.
2. y-ra rendezzük, hogy meglegyen a meredeksége=m.
3. A parabola érintője y=mx+b alakú, b paraméter.
4. Egyenletrendszer a parabola egyenletével. Behelyettesítve másodfokú egyenlet. Mivel érintőről van szó a diszkrimináns = 0. Ebből megvan b, tehát ismerjül az érintő egyenletét.
5. Felírjuk az OP egyenes egyenletét.
6. OP metszéspontja az érintővel, egyenletrsndszer: Q
7. PQ távolság.
8. Parabola egyenletéből kiolvasni a F pontot
9. Origó F távolsága.
|
| Előzmény: [1466] Füge, 2010-12-30 23:06:03 |
|
| [1470] Füge | 2011-01-02 13:20:29 |
 Igen én is így indultam neki a feladatnak, csak másodfokú egyenlet rendszer, Viéte-formula, deriválás... azért kérdeztem, hátha van szebb megoldás. Abban igazad van, hogy elfelejtettem mondani, hogy a pont a körön belül van, elnézést. Ez egy próbaérettségi feladatsorból az egyik feladat, és gondolom az első két rész kevés volt még ahhoz, hogy 16 pontot adjanak rá, ezért raktak be egy ilyen részfeladatot, hogy ismered-e a koordinátatengelyekkel párhuzamos vezéregyenesű/tengelyű parabola általános egyenletét.
|
|
| [1469] HoA | 2011-01-02 10:34:18 |
 Az origó említéséből arra következtetek, hogy ezt koordináta-geometriai feladatnak szánták. Az alakzatok tehát koordinátáikkal ill. egyenleteikkel adottak. Ekkor az is elképzelhető, a feladatkitűző arra gondolt, a P ponton átmenő legrövidebb húr meghatározásához írjuk fel a P-n áthaladó általános egyenes egyenletét m iránytangensével paraméterezve, számítsuk ki a körrel alkotott metszéspontok koordinátáit és keressük meg, e két pont távolsága melyik m-re lesz a legkisebb. ( Azt talán illett volna közölni, hogy P a körön belüli pont. )
Amit nem értek: hogy jön a harmadik kérdés az első kettőhöz? Ha adott a parabola, akkor fókusza, és így annak origótól mért távolsága is "adott" ( kiszámítható), függetlenül attól, hogy veszek-e fel egyáltalán még kört meg pontot a síkban. Ettől persze a feladat még korrekt.
|
| Előzmény: [1466] Füge, 2010-12-30 23:06:03 |
|
| [1468] Füge | 2010-12-30 23:11:42 |
 Érettségin kétlem, hogy megkérnek majd, úgyhogy marad az említés :)
|
|
| [1467] Nánási József | 2010-12-30 23:09:20 |
 Ez a Geometria 1-ben vagy 2-ben is benne van... //nekem is aktuális feladat volt nem rég
Nálunk kellett említés szerűen mondani, hogy az a legrövidebb, csak aztán meglettem kérve, hogy bizonyítsam be a táblánál.
|
|
| [1466] Füge | 2010-12-30 23:06:03 |
 Köszönöm a gyors választ. A feladat az volt, hogy adott egy parabola egy kör és egy pont. A parabola azon érintőjét keressük ami párhuzamos a P ponton átmenő legrövidebb húrral(6 pont), milyen messze van a P ponttól(5 pont) és mekkora a parabola fókuszpontjának távolsága az origótól(5 pont). Elképzelhető, hogy kell ez a bizonyítás a feladathoz, vagy elég lehet annyi, hogy triviális? Esetleg, egy egy mondatos indoklás?
|
|
| [1465] Nánási József | 2010-12-30 22:47:46 |
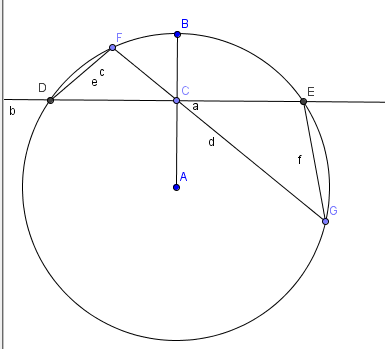
 Legyen ACD szög derékszög, ekkor DC és CE egyenlő (DE húrja a körnek)(mostantól x jelölöm)
Legyen CF y, míg CG z-vel jelölve.
DCF szög és ECG szög egyenlő, mert csúcsszögek.
DFG és DEG szögek egyenlőek, mivel azonos ívhez tartozó kerületi szögek, azaz DFC és CEG minden szöge megegyezik, így hasonlóak.
Hasonlóság miatt:


Mivel ezek valós szakaszok, emiatt az egyenletet átrendezve:


Tegyük fel hogy y+z kisebb mint 2x.
2x helyére írjuk be y+z-t, illetve az egyenletnek vegyük a kettővel képzett hányadosát. Ekkor azt várjuk, hogy hogy az egyenlet bal oldala kisebb lesz mint a jobb.

A számtani mértani közép tulajdonsága miatt, az egyenlet bal oldala nagyobb mint ajobb (S>M)

Itt tehát ellentmondás áll fent, azaz y+z>=2x.
Az egyenlet akkor és csak akkor teljesül, ha y=z, amikor pedig a merőleges húrt kapjuk vissza.
Tehát a legrövidebb húr a sugárra merőleges.
|
 |
|
| [1464] Füge | 2010-12-30 22:09:02 |
 Üdv!
Egy eléggé elemi kérdésem lenne, amire nem tudtam választ keríteni. Adott körben adott ponton átmenő húrok közül melyik a legrövidebb? Illetve az triviális, hogy a húrra merőleges, de bizonyítani nem nagyon tudtam.
(Megjegyzés: Próbaérettségi feladat emelt szint, II. rész, a feladat a,b,c, részből áll, és ezt az a, rész felénél kellene használni, szóval nem lenne rossz valami rövidebb bizonyítás)
|
|
| [1463] BohnerGéza | 2010-11-17 11:29:48 |
 Másik megoldást kaphatunk, ha észrevesszük az A*B1B2 és A*C1C2 háromszögek hasonlóságát. Területet is fölhasználva megadhatjuk, hogy AA* metszéspontja milyen osztóviszonyt ad BC-n. ...
|
| Előzmény: [1462] BohnerGéza, 2010-11-17 11:23:56 |
|
| [1462] BohnerGéza | 2010-11-17 11:23:56 |
 Az idei Kürschák-verseny 2. feladata: Az ABC háromszög AB oldalának belsejében adottak a C1 és C2 pontok, a BC oldal belsejében az A1 és A2 pontok, végül a CA oldal belsejében a B1 és B2 pontok úgy, hogy AC1<AC2, BA1<BA2, és CB1<CB2 teljesül.
Az AB1C1 és AB2C2 körök A-tól különböző metszéspontját jelölje A*, a BC1A1 és BC2A2 körök B-től különböző metszéspontja legyen B*, végül a CA1B1 és CA2B2 körök C-től különböző metszéspontját nevezzük C*-nak.
Mutassuk meg, hogy az AA*, BB* és CC* egyenesek egy ponton mennek át!
|
 |
|
| [1461] Tóbi | 2010-10-27 16:15:30 |
 Kiszámolni nem nehéz, bár azt nem látom miért igaz. Feltehető, hogy a henger tengelye a z tengely, sugara r, míg a paraboloidot az xy síktól és a P=(a,0,b) ponttól egyenlő távol lévő pontok alkotják. Ekkor ha (x,y,z) mindkét alakzatnak eleme:
x2+y2=r2
(x-a)2+y2+(b-z)2=z2
Kivonva a két sort egymásból:
2ax+2bz=a2+b2+r2
Tehát a metszet benne van a fenti síkban.
|
| Előzmény: [1460] HoA, 2010-10-27 10:56:11 |
|
| [1460] HoA | 2010-10-27 10:56:11 |
 Rég nem volt feladat. Az alábbiról sem állítom, hogy új ( RóbertGida biztos tud forrást is hozzá ) , nekem is egy korábbi KöMaL feladat kapcsán jutott eszembe:
Bizonyítsuk be, hogy egymással párhuzamos tengelyű forgási paraboloid és végtelen körhenger metszésvonala síkgörbe.
|
|
| [1459] Lóczi Lajos | 2010-10-03 22:54:39 |
 Képlet, zárt alak, stb. akkor lesz az inverzre, ha valaki bevezet erre vagy az ehhez hasonló függvényre egy új nevet és kiszámolja néhány tulajdonságát.
Az elmúlt évszázadokban ez sok tucatszor megtörtént a fontosnak bizonyult függvények esetén, amelyek nem voltak "elemi függvények". Így született meg a "speciális függvények" azóta is egyre bővülő osztálya. Rögtön világossá válik a helyzet, ha vetsz egy pillantást egy ilyen gyűjteményre, pl. itt. Ezen függvények mindegyikét hívhatod "zárt alaknak". A hozzászólásodban említett függvény inverze is zárt alakú lesz, ha elnevezed pl. ojozso(x)-nek.
|
| Előzmény: [1458] ojozso, 2010-10-03 20:17:28 |
|
| [1458] ojozso | 2010-10-03 20:17:28 |
 Köszönöm mindenkinek a segítséget a 172. feldattal kapcsolatban, egyik szemem sír (nincs elemi megoldás), a másik nevet (nem a tudásom kopott meg 30 évvel az érettségi után...). A feladatot nem én, hanem az "Élet" alkotta: egy hangszerkesztő programban a megrajzolt körív szerint kellene a dinamikát (ennek révén az átlagos hangosságot) változtatni. A változtatás mértéke nyilván valamilyen arányosságban áll a körszelet területével: minél "domborúbb" (kisebb sugarú a körív), annál nagyobb lesz az átlagos hangosság-növelés (és dinamika-csökkentés). Az elérni kívánt és az aktuális hangosság-szint hányadosa adott, ennek megfelelően adott a körszelet területe is; ebből kellene a körív sugarát meghatározni, majd ha ez megvan, a körív tetszőleges pontjának koordinátáit meghatározni (ami viszont már könnyű). Abban egyetérthetünk, hogy PONTOSAN az adott körszelet területét egy, és csakis egy bizonyos sugarú körív biztosítja: a terület és a sugár között szigorúan monoton megfeleltetés van: minél nagyobb a sugár, annál kisebb a terület. Határértékkel: ha a sugár tart végtelenhez, a terület tart 0-hoz. Képlet hiányában a sugarat próbálkozásokkal be fogom tudni "lőni" tetszőleges pontossággal a területhez (végülis számítógépes program fogja számolgatni), csak elegánsabbnak gondoltam a képlet alkalmazását, ezért tettem fel a feladatot.
A matematikához visszatérve, úgy gondolom, előbb-utóbb lesz zárt alak az általam felvetett és az ahhoz hasonló (pl. a későbbiekben említett) függvény INVERZÉRE is, de az NEM elemi módszerekkel lesz levezetve!
|
|
| [1457] Lóczi Lajos | 2010-10-03 15:28:45 |
 Ahogyan már el is hangzott, ezek olyan elemi függvények, amelyeknek az inverze nem elemi függvény. Persze a függvény is és az inverze is hatványsorba fejthető például, amiből közelítő megoldásokat ki lehet olvasni.
|
| Előzmény: [1455] HoA, 2010-10-01 23:02:52 |
|
| [1456] jonas | 2010-10-02 17:18:57 |
 Az én kedvenc példám az efféle egyenletekre az, amikor egy ellipszispályán keringő bolygó helyét akarjuk megadni az idő függvényében. Ez általában egy sinx=ax+b típusú egyenletre vezet, aminek elemi függvényekkel nem lehet megtalálni a megoldását. A helyből az időt viszont vissza lehet számolni csak elemi függvényekkel.
|
|
| [1455] HoA | 2010-10-01 23:02:52 |
 Kedves matematikus fórum látogatók! Igen, azt hiszem itt az a kérdés, van-e valamilyen fogalom az ilyen értelemben nem invertálhazó függvényekre. Vagyis amikor y kifejezhető zárt alakban x függvényeként, például
y=x+sin(x)
, de x nem adható meg zárt alakban y függvényeként.
|
| Előzmény: [1454] Gubbubu, 2010-10-01 22:05:05 |
|
| [1454] Gubbubu | 2010-10-01 22:05:05 |
 Nem is az a fő baj, hogy transzcendens (tkp. az abszolútértékes egyenletek is transzcendensek, mégis szépen meg lehet őket oldani :-). Talán érdemes lenne a Wikipédiában megnézni az implicitfüggvény-tétel c. szócikket, az én ismerettáramban ez a legközelebbi fogalom, aminek egyáltalán köze lehet a feladatodhoz, bár hogy alkalmazható-e ... ? Amúgy a probléma maga szép, amit feladtál. :-)
|
| Előzmény: [1453] nadorp, 2010-10-01 12:15:55 |
|
| [1453] nadorp | 2010-10-01 12:15:55 |
 A végeredményed jó, de ebből r-t szerintem nem lehet kifejezni, mert ez egy transzcendens egyenlet. ( hasonlóan pld. az x=3sinx egyenlethez). Csak közelítő megoldás van.
|
| Előzmény: [1452] ojozso, 2010-09-29 20:20:00 |
|
| [1452] ojozso | 2010-09-29 20:20:00 |
 Köszi a választ!
Én is próbálkoztam a megoldással, mielőtt feltettem a Fórumra a feladatot, csak nem akartam befolyásolni vele senkit.
Most leírom, meddig jutottam el.
A körszelet területe (t): Tkorszelet=Tkorcikk-TQOCharomszog.
A HÁROMSZÖG TERÜLETE:
 , mivel e=f=r , mivel e=f=r
OFQ derékszögű háromszögben (F az OC szakasz felezőpontja) OQF szög  fele. Szinusz definíciója alapján: fele. Szinusz definíciója alapján:
 , mivel , mivel  (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója). (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója).
 . (Kétszeres szög szinusza). A . (Kétszeres szög szinusza). A  azonosságból: azonosságból:  , melyet behelyettesítve kapjuk: , melyet behelyettesítve kapjuk:
 . Beírva . Beírva  -re kapott -re kapott  értéket: értéket:
 . Egyszerűbb alakra hozva megkapjuk, hogy . Egyszerűbb alakra hozva megkapjuk, hogy 
A háromszög területe tehát:
| (1) |  |
A KÖRCIKK TERÜLETE:
 ( ( radiánban.), vagyis: radiánban.), vagyis:
| (2) |  |
A KÖRSZELET TERÜLETE:

És itt a végállomás! Fogalmam sincs, hogyan lehetne ebből r-et kifejezni, már csak azért sem, mert r az arcsin argumentumában is szerepel és nem tudom, hogyan lehet onnan kihozni.
Innentől kéne segítség. Ráadásul abban sem vagyok biztos, hogy eredményem ekvivalens-e a Tieddel.
|
 |
| Előzmény: [1450] Gubbubu, 2010-09-28 12:19:53 |
|
|
| [1450] Gubbubu | 2010-09-28 12:19:53 |
 Az első feladatra nekem az 
A megoldás leírásához szükséges időm most túl kevés, estefelé vagy pár nap múlva talán; így a képzeletbeli margón marad :-).
Szükséges lenne természetesen az ért. tartományok vizsgálata is, továbbá esetleges geometriai diszkusszió. Nagy vonalakban az történt, hogy kiszámolod a körcikk területét (ez egyszerű egyenes arányosság), majd az ún. trigonometrikus területképlettel az OAC háromszögét, és kivonod a kettőt egymásból. Ezután kifejezed az omega szöget az r segítségével (ehhez ügyeskedni kell az addíciós tételekkel), így eltüntetvén az omegát a képletből (opcionális, az arcsin-elt kifejezés egyébként maga a szinusz omega).
|
| Előzmény: [1449] ojozso, 2010-09-27 18:49:48 |
|
| [1449] ojozso | 2010-09-27 18:49:48 |
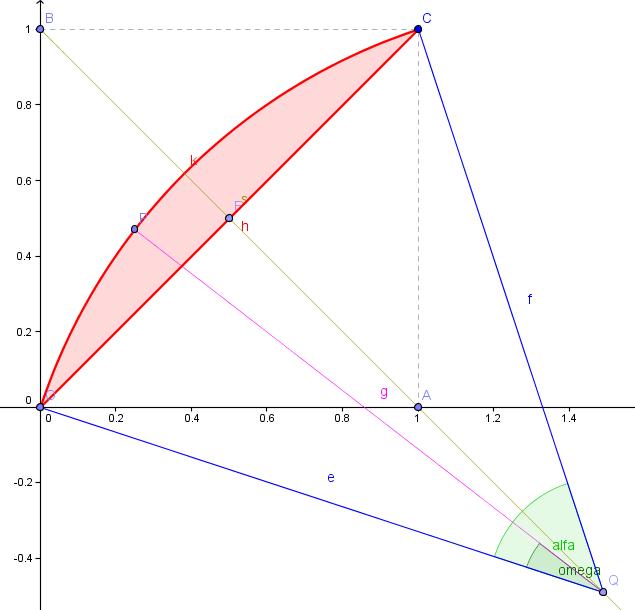
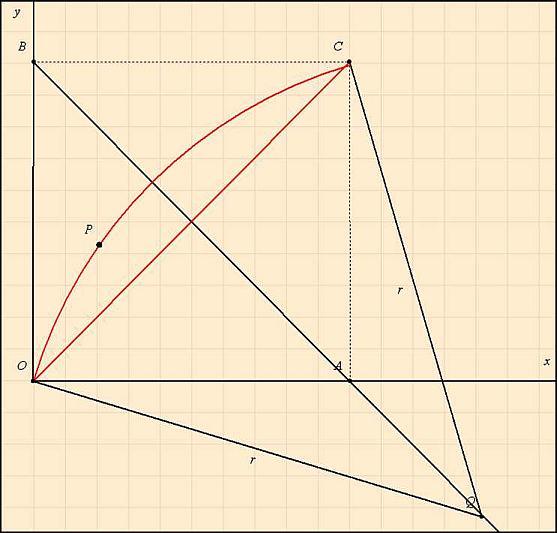
 Sziasztok!
Új vagyok itt és adódott egy probléma, melyen nem tudok túljutni, de Nektek bizonyára menni fog... Tehát:
172. feladat
Jelöljük O-val az origót (0;0), A-val az (1;0), B-vel a (0;1) és C-vel az (1;1) pontokat. Az AB szakasz A ponton túli meghosszabításával kapott félegyenesen AB szakaszon kívül vegyünk fel egy tetszőleges Q (u;v) pontot. QO=QC=r sugárral rajzoljuk fel a Q középpontú OC körívet. Ezen a köríven vegyünk fel egy tetszőleges P (x;y) pontot. Az OC szakasz és az OC körív által (pirossal) határolt körszelet területét jelöljük t-vel, az OQP szöget pedig omega-val (QP szakasz sajnos, lemaradt a rajzról.)
Határozzuk meg az adott t területű körszelethez tartozó r sugarat!
Írjuk fel az adott adott t területű körszelethez tartozó körív tetszőleges P pontjának koordinátáit r és omega függvényében!
|
 |
|
|
| [1447] Csimby | 2010-09-08 02:16:06 |
 Szóval mindenképpen ajánljuk, hogy megrendeld a lapot és csináld a pontversenyt - szerintem rengeteget lehet tanulni belőle - de itt a fórumon többnyire más feladatok kerülnek elő!
|
| Előzmény: [1446] BohnerGéza, 2010-09-08 00:59:23 |
|
| [1446] BohnerGéza | 2010-09-08 00:59:23 |
 Természetesen sok a lapban megjelenő feladat is előkerül itt, de a kettő nem fedi egymást.
A Lapban sok érdekes feladat van különböző nehézségűek csoportosításával. Az "A" jelűek nehezek, könnyebbek a "B"-k, kezdőknek a "C" jelűek valók, illetve kifejezetten kilencedikeseknek szólnak a "K" jelűek. Számítástechnikai és fizikai rovat is található sok érdekes feladattal.
A feladatok mellett nívós cikkek is vannak, sok kitűzött feladat megoldása is szerepel, valamint a pontverseny állása is félidőben, illetve a végeredménye.
|
| Előzmény: [1443] kuklic, 2010-09-06 18:16:49 |
|
| [1443] kuklic | 2010-09-06 18:16:49 |
 A feladatokat amiket itt megoldtok, a megrendelt komal lapból csináljátok? mert ha igen akkor megrendelem én is :)
|
|
| [1442] BohnerGéza | 2010-09-04 11:44:38 |
 Néhány megjegyzés a 171. feladathoz, és HoA szép megoldásához:
- Ha érintőkörökkel definiálunk valamit, érdemes lehet analóg feladatokat is megfogalmazni! ... (Valaki a 171. feladathoz?)
- A trapéz átlóinak metszéspontján átmenő, az alapokkal párhuzamos egyenesnek a trapézban lévő szakasza az alapok harmonikus közepe. (Ezt a szakaszt felezi az átlók metszéspontja, tehát a feladatban a magasság felezőpontja szerepel.) Ebből is folytatható a "volt egyszer..." helyett HoA megoldása.
Érdemes lehet tudni:
Ha a trapéz szárait az alapok arányában osztjuk, az osztópontokat összekötő szakasz az alapok mértani közepe. (Ha fordított arányban osztjuk, azt nem tudom, érdemes lehet kiszámolni!)
A trapéz szárainak felezőpontjait összekötő szakasz az alapok számtani közepe.
Ha a trapézt az alapokkal párhuzamosan úgy osztjuk ketté, hogy a területét felezzük, az osztóvonal az alapok négyzetes közepe lesz.
Ezekkel két számra igazolhatóak a szereplő közepekre az egyenlőtlenségek.
|
| Előzmény: [1441] HoA, 2010-08-19 13:19:44 |
|
| [1441] HoA | 2010-08-19 13:19:44 |
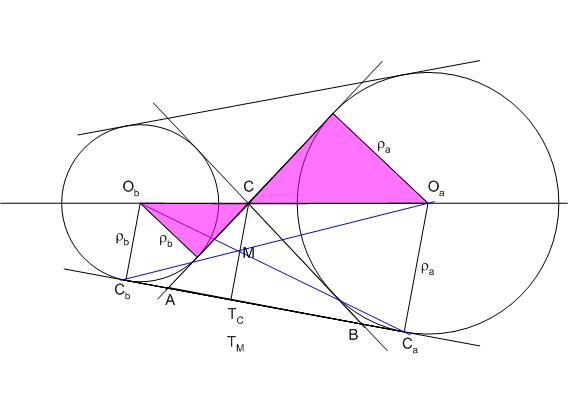
 Egészítsük ki az ábrát a hozzáírt körökkel és közös érintőikkel. A lila háromszögek hasonlóságából és a párhuzamos szelők tételéből  . Vagyis Tc a hozzáírt körök sugarainak arányában osztja a CaCb szakaszt. Az OaObCbCa derékszögű trapéz átlóinak M metszéspontjából CaCb -re bocsátott merőleges talppontja legyen TM Mivel CaTM és CbTM az OaCaM és ObCbM hasonló háromszögek megfelelő magasságai, ezek aránya is . Vagyis Tc a hozzáírt körök sugarainak arányában osztja a CaCb szakaszt. Az OaObCbCa derékszögű trapéz átlóinak M metszéspontjából CaCb -re bocsátott merőleges talppontja legyen TM Mivel CaTM és CbTM az OaCaM és ObCbM hasonló háromszögek megfelelő magasságai, ezek aránya is  , TM és Tc egybeesik, M valóban rajta van CTc -n , TM és Tc egybeesik, M valóban rajta van CTc -n
Volt egyszer egy KöMaL feladat, amelyik azt kérdezte, megszerkeszthető-e a háromszög ha adott két hozzáírt kör sugara és a harmadik oldalhoz tartozó magasság. Eredményül persze kijött, hogy a három szakasz nem független, a magasság a két sugár harmonikus közepe, így vagy nincs megoldás vagy a feladat határozatlan. Ezt ismertnek feltételezve, a B 4276 annak bizonyítását kéri, hogy a harmonikus közép nem nagyobb a mértani középnél, ami e fórum látógatói számára érdektelen.
BohnerGéza ábrája viszont úgy is értelmezhető, hogyan szerkeszthetjük meg egyszerűen két szakasz harmonikus közepét. Hirtelenjében erre nem látok jobb megoldást.
|
 |
| Előzmény: [1440] BohnerGéza, 2010-08-04 02:02:39 |
|
| [1440] BohnerGéza | 2010-08-04 02:02:39 |
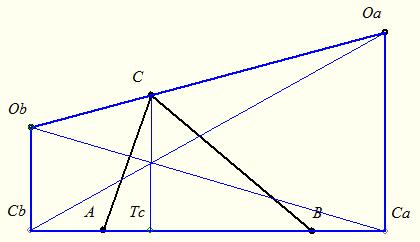
 171. feladat: A B.4276 feladattal kapcsolatban:
Az ABC háromszög két hozzáírt körének középpontja Oa és Ob, ezek érintési pontja az AB oldalon Ca és Cb A C-ből induló magasság CTc. Bizonyítandó, hogy OaCb és ObCa a CTc szakaszon metszik egymást.
|
 |
|
| [1439] gida1 | 2010-07-22 11:47:36 |
 Nagyon köszönöm, Jonas!
|
|
|
| [1437] gida1 | 2010-07-22 01:27:14 |
 Sziasztok! A segítségeteket kérném. Mi a magyar megfelelője az angol PERMUTOHEDRON-nak? Milyen éder? Segítségül egy link: http://en.wikipedia.org/wiki/Permutohedron
És mi az a BIPARITE GRAPH / BIGRAPH? http://en.wikipedia.org/wiki/Bipartite
Segítségeteket előre is köszönöm!
|
|
|
| [1435] S.Ákos | 2010-07-10 21:13:54 |
 170./a: k körre vonatkozó inverzióval, vázlatosan
AB képe az AOBFE kör, az O-n átmenő 3 kör (AEO, CDO, FBO képe 1-1 egyenes, rendre AE, CD, FB, AOB, AOC, COD, DOB egyenlőszárú háromszögek. Az állítás az, hogy EA és BF azonos szöget zár be CD-vel. Innét szögszámolással adódik, hogy tényleg egyenlő a két szög, (mondjuk legyen BAO =ABO =ABO = = és AOE és AOE = = 1, COD 1, COD = = 1, DOB 1, DOB = = 3). 3).
|
 |
| Előzmény: [1431] HoA, 2010-06-24 12:43:03 |
|
| [1434] sakkmath | 2010-07-10 20:46:09 |
 Túlbonyolítottam. Rájöttem, hogy nem kell az inverzió. Elég azt látni, hogy mivel a k3 körben N1 N2 húr, ezért őt merőlegesen felezi MO. Ezért az N1 N2 O háromszög egyenlő szárú, stb. (Elnézést.)
|
| Előzmény: [1433] sakkmath, 2010-07-10 18:59:21 |
|
|
|
| [1431] HoA | 2010-06-24 12:43:03 |
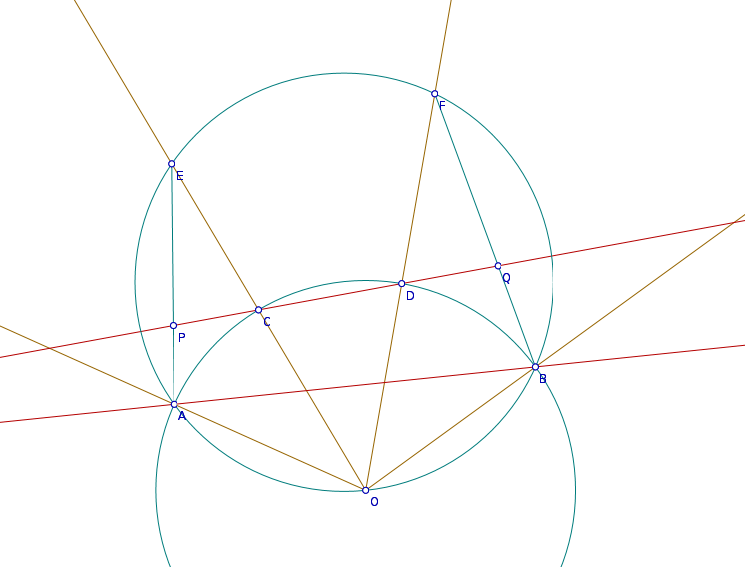
 170. feladat Az O középpontú k kört az e szelő az A és B pontokban metszi.Az AB ív C és D pontjába húzott sugár metszéspontja e-vel E és F.
a)Igazoljuk, hogy az AEO pontok k1 köre és a BFO pontok k2 köre azonos szögben metszi az OCD pontok k3 körét. Az O-tól különböző metszéspontok P és Q.
b)Bizonyítsuk be, hogy a k1-et P-ben és k2-t Q-ban érintő kör e-t is érinti.
|
 |
|
| [1430] HoA | 2010-06-16 12:25:39 |
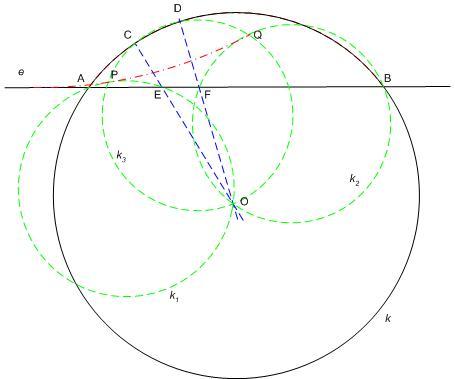
 A 165. [1422] feladat megoldása. E fórum olvasóinak, feladatmegoldóinak sokkal tömörebben is elég lenne, de szerintem tanításban jól használható, így kicsit részletesebben írok.
a) Legyen egyelőre ABC beírt körének érintési pontja AB-n C* . C* az az AB szakaszon lévő pont, melyre az A-tól és B-től mért távolságok különbsége ugyanakkora, mint C-re. Ennek igazolásához elég a csúcsokból a beírt körhöz húzható érintőszakaszok s-a és s-b kifejezéseire hivatkozni. Megmutatjuk, hogy ez C1-re is igaz, tehát C*=C1. Igazoljuk, hogy BC1–AC1=BC-AC , vagyis [BC1–AC1]–[BC-AC]=0 . Az ábrán a kisbetükkel jelölt egyenlő érintőszakaszokkal, valamint n=d+g+h és j+m=f+g+h felhasználásával [(k+j+m)–(e+f)]–[(k+n)-(d+e)]=[j+m-f]-[n-d]=[g+h]-[g+h]=0
b) Ennek alapján megállapíthatjuk, hogy van olyan A és B fókuszú hiperbola, mely C-n és C1-en is áthalad. A fenti képletet átrendezve [BC-BC1]–[AC–AC1]=0 , ami viszont azt jelenti, hogy van olyan C és C1 fókuszú hiperbola, mely A-n és B-n is áthalad. Erről kell belátni, hogy P-n is áthalad, vagyis [PC-PC1]–[AC–AC1]=0 . Az ábra érintőszakaszaival [(d+g)-(g+f)]–[(d+e)–(e+f)]=[d-f]–[d–f]=0 . A háromszögbe eső parabolaív minden P’ pontja kiadódik P-nek, ha D-t CP’ és AB metszéspontjának választjuk.
c) A két kör közös belső érintői szimmetrikusak a két kör centrálisára, a centrális felezi a CPC1 szöget, tehát érintője a hiperbolának. Egyenlő sugarak esetén a centrális párhuzamos AB-vel.
d) Visszavezettük a feladatot adott hiperbola adott irányú érintőjének és a P érintési pontnak a szerkesztésére. Tekintsük a hiperbolát mint az F1 középpontú vezérkört érintő és F2-n áthaladó körök középpontjának mértani helyét. F2-nek a P-beli érintőre vett F2’ tükörképe a vezérkör és a PF1 egyenes metszéspontja, F2F2’ merőleges az érintőre. A szerkesztés: Húzzunk F2-n át merőlegest egy érintőirányú egyenesre, ennek a vezérkörrel alkotott (egyik) metszéspontja F2’ , F2F2’ felező merőlegese az e érintő, e és F1F2’ metszéspontja a P érintési pont. Feladatunkban A a hiperbola pontja, az A körüli, C1-en áthaladó kör és az AC szakasz B1 metszéspontja rajta van a C körüli vezérkörön. Az ABre C1-ben emelt merőleges és a C körüli CB1 sugarú kör (egyik) metszéspontja legyen Q . A D pont CQ és AB metszéspontjaként adódik.
Ehhez a szerkesztéshez most már a hiperbola felhasználása nélkül is eljuthatunk. Ha a két kör sugara egyenlő, akkor közös belső érintőik tükrösek az AB -val párhuzamos centrálisra. Legyen Q a PC szakasznak az a pontja, melyre PQ=PC1. PQC1 egyenlőszárú háromszög C1Q alapja merőleges AB-re, Q rajta van az AB -re C1-ben emelt merőlegesen. Másrészt CQ=PC–PC1=AC–AC1 . Az AC szakaszra ráforgatva az AC1 távolságot a végpont legyen B1 . CB1=AC–AC1 . Q rajta van a C körüli CB1 sugarú körön, innen a szerkesztés a fenti.
|
 |
| Előzmény: [1422] BohnerGéza, 2010-06-03 16:31:30 |
|
|
| [1428] BohnerGéza | 2010-06-05 13:01:10 |
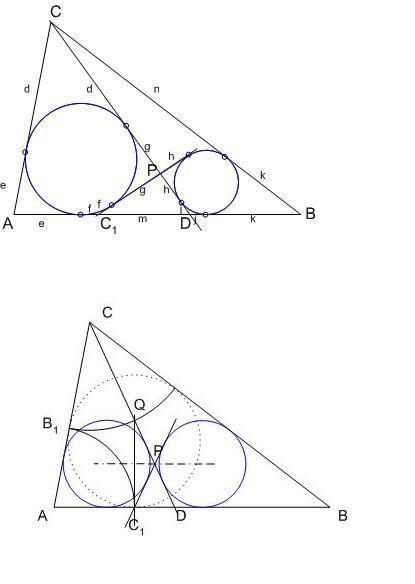
 Felhasználandó a 168. feladatban:
169. feladat: Az ABC háromszög AC illetve BC oldalán vegyük föl a D illetve E pontot úgy, hogy az AEC és BCD beírt köre azonos legyen: k1. Az AE és BD metszéspontja legyen F. Jelölje k2 az ABF beírt körét, érintse ez C1-ben AB-t. Igazoljuk, ha a CA-n mozgatjuk D-t (E és F megfelelően mozog), akkor C1 nem mozog. (Az ABC beírt körének pontja.)
|
 |
| Előzmény: [1427] BohnerGéza, 2010-06-05 12:53:18 |
|
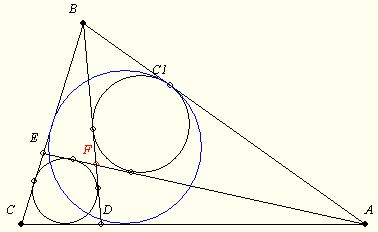
| [1427] BohnerGéza | 2010-06-05 12:53:18 |
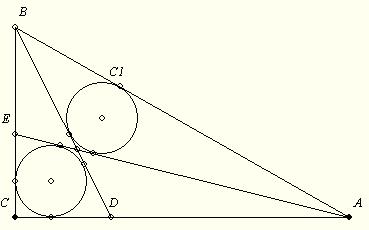
 Valóban! Pontosítva az [1406]-ban említett AD-feladatot:
168. feladat: Az ABC C-nél derékszögű háromszög AC illetve BC oldalán vegyük föl a D illetve E pontot úgy, hogy az AEC és BCD beírt köre azonos legyen: k1. Az AE és BD metszéspontja legyen F. Jelölje k2 az ABF beírt körét.
Fejezzük ki az ABC oldalai segítségével k1 sugarát, ha egyenlő a k2-ével!
|
 |
| Előzmény: [1424] HoA, 2010-06-05 09:01:13 |
|
|
| [1425] BohnerGéza | 2010-06-05 11:26:21 |
 167. feladat: Tekintsük az AFG háromszög k körülírt és C középpontú beírt körét. Legyen B a k tetszőleges pontja, a B-ből a beírt körhöz húzott érintők messék k-t még D-ben illetve E-ben. Igazoljuk, hogy DE érinti a beírt kört, azaz AFG és BDE beírt köre azonos.
Az [1409]- ben lévő 165. feladat bizonyításához elég megmutatni: Ha B-t k és AC másik metszéspontjának vesszük, szimmetria miatt elég belátni, hogy B egyenlő távol van F-től és C-től.
|
| Előzmény: [1409] HoA, 2010-04-23 17:24:22 |
|
|
|
| [1422] BohnerGéza | 2010-06-03 16:31:30 |
 A B.4269 feladattal kapcsolatban keletkezett a hozzászólás. Érdemes a "Lejárt határidejű KÖMAL feladatokról" című téma 552. hozzászólását is megnézni.
Az ABC háromszög AB oldalán mozgatjuk a D pontot. Az ADC és DBC beírt körének másik (nem CD) közös belső érintője AB-t a C1-ben metszi. A két belső érintő metszéspontja P. Mutassuk meg a következőket:
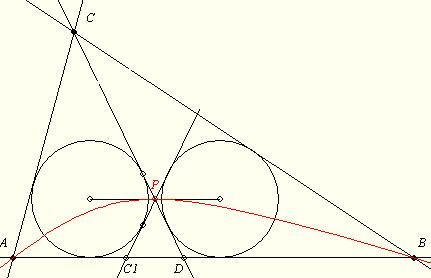
165. feladat: a.) Igazoljuk, hogy C1 nem függ D-től! (ABC beírt körének pontja)
b.) Igazoljuk, hogy a P pontok halmaza a C és C1 fókuszú és A-n átmenő hiperbola A-n (és B-n) átmenő ágának a háromszögbe eső része!
c.) Igazoljuk, hogy a két kör sugara akkor egyforma, ha a hiperbola P-ben húzott érintője párhuzamos AB-vel!
d.) A fentiek alapján szerkesztendő az a D, melyre a két kör sugara egyenlő!
|
 |
|
| [1421] kuklic | 2010-06-01 22:03:10 |
 Nagyon szépen köszönöm :) Elég jó vagy :D ezt magamtól nem biztos, hogy megláttam volna :)
|
|
| [1420] HoA | 2010-06-01 17:01:37 |
 A négy hasonló derékszögű háromszögből is szépen kijön, de talán a legegyszerűbb, ha észrevesszük, hogy az A1 -nél és B1 -nél lévő derékszögek miatt A1 és B1 rajta van AB Thálesz-körén, így ABA1B1 húrnégyszög, a szelőtétel éppen a kívánt egyenlőséget adja.
|
| Előzmény: [1419] kuklic, 2010-06-01 16:38:56 |
|
| [1419] kuklic | 2010-06-01 16:38:56 |
 Hello mindenki Egy kis segítséget kérnék. Ezzel a feladattal elakadtam:
Az ABC hegyesszögű háromszög A-ból induló magasságvonalának BC-vel való metszéspontja A1, B-ből induló magasságvonalának AC-vel való metszéspontja B1, magasságpontja M. Igazolja, hogy AM*MA1=BM*MB1!
|
|
| [1418] Hajba Károly | 2010-04-29 00:24:00 |
 Én egy kicsit másképpen oldottam meg, de HoA ábráját felhasználva már könnyebben megérthető.
A belső ötszög belső szögei: 5*180-360 = 540. Azaz az ötszögön belül kijelölsz egy pontot és 5 háromszöget képezel az öt pontból 2-2 szomszédos pont ill. a központi pont segítségével. Ez az öt háromszög teljesen kitölti a belső ötszöget. Az öt háromszög belső szögeinek összegéből levonod a központi ponthoz tartozó 360 fokot és így kapod az ötszög belső szögeinek összegét. Eddig talán nem is volt újdonság.
A külső szögeinek összegét úgy kapjuk, hogy az öt pont teljes szögeiből levonjuk a belső szögeket. 5*360-540 = 1260.
Most a belső ötszög külső oldalára 5 háromszöget illesztünk úgy, hogy épp a kívánt csillagötszöget adja ki. Itt a háromszögek belső 2-2 szögei részei az ötszög külső szögei tartományának. S közöttük épp a csúcsszög miatt épp a belső szög a különbség. Azaz, ha az ötszög külső szögeinek összegéből levonom a belső szögeinek összegét, akkor a háromszögek a belső ötszöggel érintkező 2-2 szög összegét kapjuk.
Vagyis ha az 5 háromszög szögösszegéből levonjuk a belső ötszög külső szögeit és hozzáadjuk a belső szögeit, akkor épp a csúcsszögek összegét kapjuk.
5*180 - 1260 + 540 = 180
Ha lesett a tantusz vagy kisült az isteni szikra, akkor már egyszerűbb, mint ahogy most leírtam.
|
| Előzmény: [1415] Cseri, 2010-04-27 23:46:12 |
|
|
| [1416] HoA | 2010-04-28 13:36:46 |
 Megoldásod annyiban vázlat, hogy abból, hogy a két háromszög beírt körének C a középpontja, még nem következik, hogy a hatszögbe kör írható, csak akkor, ha azt is igazoljuk, hogy a háromszögek beírt köreinek egyenlő a sugara - a beírt körök egybeesnek.
|
| Előzmény: [1414] lorantfy, 2010-04-27 21:33:10 |
|
| [1415] Cseri | 2010-04-27 23:46:12 |
 Üdvözlök mindenkit!
En egy uj vendeg vagyok ezen a weboldalon. Es lenne egy kerdesem. Esetleg valaki tudna nekem segiteni??!! Egy nem szabalyos csillagötszögröl ( pentagramma ) van szo. Be kell bizonyitani, hogy az öt csillagcsucsban levö szögeinek összege 180 fok. Ezt a szabalyos csillagötszögben be tudom bizonyitani,de a nem szabalyosban nem. Van esetleg valakinek ötlete?? Segitsegeteket elöre is köszönöm. Cseri Nemetorszagbol
|
|
| [1414] lorantfy | 2010-04-27 21:33:10 |
 Megoldásvázlat a 165.höz: A k körben AD és AE ívek valamint a BG és BF ívek egyenlők, mert a k1 illetve a k2 kör vágja ki őket. Így az AB húr az AFG és BDE háromszögben is szögfelező. FAC szög=GAC szög és AB a k2 körnek is szimmetria tengelye, így azonos íveket vág ki a k2 körből. Ez már bizonyítja, hogy GC is szöfelező, így C lesz az AFG háromszög beírt körének középpontja. Hasonlóan a másik, BDE háromszögre is, vagyis az említett hatszögnek is beírt köre. Ahogy lesz időm rajzolok egy ábrát. Jó példa! Köszönet érte!
|
| Előzmény: [1409] HoA, 2010-04-23 17:24:22 |
|
| [1413] Rozali | 2010-04-26 08:25:08 |
 Szia! Nagyon szépen köszönöm a segítséget !! Így már menni fog remélem!
|
|
| [1412] Tauthorne | 2010-04-25 16:18:50 |
 Bocsi, előző üzenetben véletlenül elírtam a legvégét: 7x+5y=-13 az egyenlete
|
|
| [1411] Tauthorne | 2010-04-25 16:14:57 |
 Szia! Mivel merőleges az adott egyenesre, ezért annak normálvektora (5,-7) az pont jó lesz a keresett egyenes irányvektorának. Az irányvektoros egyenlet pedig: v2x0-v1y0=v2x-v1y ,beirva a számokat: (-7)*(-4)-5*3=-7x-5y tehát:7x+5y=43
|
|
| [1410] Rozali | 2010-04-25 13:46:24 |
 Sziasztok! Megcsinálná ezt valaki nekem? Adjuk meg annak az egyenesnek az egyenletét, amely merőleges az 5x-7y=-17 egyenletű egyenesre,és átmegy a P(-4;3) ponton!
és ha kérhetem magyarázza is el mert lemaradtam és nem értem!!!!!!
Előre is nagyon köszi holnapra kellene!
|
|
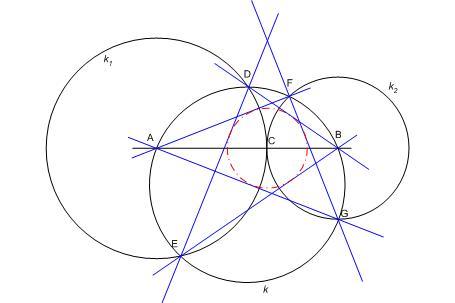
| [1409] HoA | 2010-04-23 17:24:22 |
 Javaslat a 165. feladatra:
A k kör AB húrjának belső ponja C . Az A középpontú, C-n áthaladó k1 kör és k metszésponjai D és E, a B középpontú, C-n áthaladó k2 kör és k metszésponjai F és G . Bizonyítsuk be, hogy az AF , AG, BD , BE , DE és FG egyenesek által határolt hatszögbe C középpontú kör írható.
|
 |
|
|
| [1407] HoA | 2010-04-23 14:47:56 |
 1) Ha F a BC oldal belső pontja, akkor AF és BC metszéspontja F. Nem AF és BE metszéspontjáról van szó?
2) Ekkor viszont CFME nem lehet húrnégyszög, hiszen C-nél derékszögű, tehát M-nél is derékszögűnek kéne lennie, de a definíció szerint M a háromszög belső pontja és így az AB feletti Thálesz-körnek is belső ponja, vagyis FME szög = AMB szög > 90 fok. Mivel belé írható körről írsz, nem inkább érintőnégyszög?
|
| Előzmény: [1406] m2mm, 2010-04-23 14:29:17 |
|
| [1406] m2mm | 2010-04-23 14:29:17 |
 Tegnap volt kitűzve Arany Dánielen a következő(nem szó szerint ez volt a szöveg): Egy ABC C-ben derékszögű háromszög AC oldalának E, BC oldalának F belső pontja, AF és BC metszéspontja M. CFME húrnégyszög, a belé írható körének sugarának nagysága megegyezik AMB háromszög beírt körének sugaráéval. Fejezzük ki a háromszög oldalaiból a körök sugarának nagyságát.
|
|
|
| [1404] m2mm | 2010-04-06 18:47:47 |
 Üdv!
Egy egységsugarú körbe írt szabályos n-szög egyik csúcsát összekötjük az összes többivel. Bizonyítsuk be, hogy e szakaszok hosszainak szorzata éppen n.
|
|
| [1403] HoA | 2010-03-30 16:50:55 |
 Két megjegyzés:
1) Jogos az észrevétel, a kitűzés így lett volna korrekt: Adott két szakasz, a és b , b>0 , 0 a a b ... b ...
2) Vegyük észre, hogy a jobboldalt  függvényének q=f( függvényének q=f( ) tekintve az szimmetrikus a ) tekintve az szimmetrikus a  =22,5o;q=1/2 pontra, vagyis f(45o- =22,5o;q=1/2 pontra, vagyis f(45o- )=1-f( )=1-f( ) , ami BohnerGéza megoldásában is tükröződik. ) , ami BohnerGéza megoldásában is tükröződik.
Ez és a nevezőben szereplő 1+tg( ) talán indokolják, hogy a kifejezést tg( ) talán indokolják, hogy a kifejezést tg( ) és tg(45o- ) és tg(45o- ) szerepeltetésével alakítsuk át. ) szerepeltetésével alakítsuk át.

, amiből a.tg =(b-a).tg(45o- =(b-a).tg(45o- ) . Ennek alapján a szerkesztés: Vegyük fel a b hosszúságú AB szakaszt, A-ból B felé mérjük rá az a hosszúságú AT szakaszt. T-ben emeljünk m merőlegest AB-re, ennek T-től különböző pontja legyen C. Az ABC ) . Ennek alapján a szerkesztés: Vegyük fel a b hosszúságú AB szakaszt, A-ból B felé mérjük rá az a hosszúságú AT szakaszt. T-ben emeljünk m merőlegest AB-re, ennek T-től különböző pontja legyen C. Az ABC A-nál lévő szöge megfelel A-nál lévő szöge megfelel  -nek, ha a B-nél lévő szög 45o- -nek, ha a B-nél lévő szög 45o- , vagyis ha C-nél 135o-os szög van. C tehát m és az AB szakasz 135o-os látószögű körívének metszéspontja. , vagyis ha C-nél 135o-os szög van. C tehát m és az AB szakasz 135o-os látószögű körívének metszéspontja.
Hogyan kapcsolódik a fenti átalakítás a B. 4244 feladathoz?
|
| Előzmény: [1390] BohnerGéza, 2010-03-16 13:03:46 |
|
|
| [1401] Hajba Károly | 2010-03-21 22:04:33 |
 A könyvet a Typotex 2001-ben újra kiadta, de már elfogyott. Egy részét e-könyv formájában be lehet szerezni vagy antikváriumban kutakodni.
Ha küldtök címet, beszkennelem a feladatot és a megoldást.
|
|
| [1400] Róbert Gida | 2010-03-21 17:58:54 |
 A körös és a félsíkos példa a 40. Körre az optimális d, félsíkra  , ez utóbbi bizonyítás nélkül. (d a kör átmérője, illetve másiknál a félsík és a turista távolsága legfeljebb d). , ez utóbbi bizonyítás nélkül. (d a kör átmérője, illetve másiknál a félsík és a turista távolsága legfeljebb d).
|
| Előzmény: [1398] HoA, 2010-03-21 09:36:06 |
|
|
| [1398] HoA | 2010-03-21 09:36:06 |
 A téma iránt érdeklődőknek javaslok két magyar nyelvű anyagot:
Tóth Gábor: Bellman feladata KÖMAL 1982. 7. szám 53. oldal
és az ebben hivatkozott
Skljarszkij-Csenov-Jaglom: Válogatott feladatok és tételek ... 2/2 Geometriai egyenlőtlenségek ... 40. feladat
Remélem, a fórum olvasói számára hozzáférhetőek. ( Nekem a könyvet nem sikerült megszereznem, ha egy bemásolás erejéig valakitől kölcsönkaphatnám, megköszönném )
|
| Előzmény: [1396] jonas, 2010-03-17 09:53:10 |
|
| [1397] HoA | 2010-03-17 16:27:31 |
 Igen, a probléma különböző alakú erdőkre ismert. Én azzal a változattal találkoztam először, ahol az erdő egy félsík és azt tudom, hogy a szélétől max. R méterre vagyok, de a határegyenes irányát nem tudom. Mi az a legrövidebb útvonal, amit követve ( tetszőleges kezdőirányban indulva ) biztosan kijutok az erdőből? Mint a hivatkozott cikk elejéből látható, a másik kivesézett eset a két, adott távolságú párhuzamos közötti erdősáv.
http://www.jstor.org/pss/4145038
|
| Előzmény: [1396] jonas, 2010-03-17 09:53:10 |
|
| [1396] jonas | 2010-03-17 09:53:10 |
 Ezt nem értem. Ha az erdő kör alakú, akkor elég 2R hosszan egyenesen előre mennik, és kijutsz. Érdekesebb lenne, ha mondjuk az erdő egy félsík, és felteszed, hogy a kezdeti állapotban legfeljebb R mélységig vagy benne.
|
| Előzmény: [1392] psbalint, 2010-03-16 22:51:13 |
|
| [1395] psbalint | 2010-03-16 23:58:07 |
 a körvonalon elindulás nekem nem jutott eszembe. ha jól számoltam, akkor a négyzetes esetre R(1+2gyök2), a szabályos háromszögesre pedig R(1+2gyök3) jön ki, szóval mindegyiknél jobb az R*pi. egyébként ez az R*pi csak egy (jó) ötlet, vagy bizonyított, hogy ez az optimális?
|
| Előzmény: [1394] BohnerGéza, 2010-03-16 23:32:35 |
|
| [1394] BohnerGéza | 2010-03-16 23:32:35 |
 [1392]: Jó lett volna, ha támpontként a szükséges utat a felvetett esetekhez megadtad volna. Egy egyszerű tipp: helyünkön átmenő R sugarú körön elindulva R-szer pí út alatt biztosan kiérünk.
|
| Előzmény: [1392] psbalint, 2010-03-16 22:51:13 |
|
|
| [1392] psbalint | 2010-03-16 22:51:13 |
 meg még eszembe jutott valami, amit valószínűleg itt olvastam, de nem találom. adott egy R sugarú erdő, amiben el vagyunk veszve. milyen útvonalat járjunk be, hogy bárhol is vagyunk az erdőben, kijussunk belőle (a legrövidebb út)? valaki tudja, hol lett ez a feladat tárgyalva? vagy a megoldást? én most utánagondolva csak addig jutottam, hogy berajzoltam a körbe egy négyzetet meg egy szabályos háromszöget, melyeknek 3 ill. 2 csúcsát érintve (a középpontjukból indulva) egy-egy jó úthoz jutunk, ahogy látom, és amelyek közül a négyzetes tűnik rövidebbnek. ez lenne a jó megoldás? miért? miért nem? hilfe!
|
|
| [1391] psbalint | 2010-03-16 21:53:51 |
 Egy feladat, kérdés, vagy valaki mondjon rá valamit: Rajzoljunk egy lapra egy S betűt, de úgy, hogy szép függőleges legyen, és két félkörből tevődjön össze, melyeknek az átmérője legyen 1 egység. Kössük össze az S betű legmagasabban fekvő pontját a szimmetriaközéppontjával, és ennek a szakasznak a felezőpontja legyen F. Elkezd lefelé csúszni a szakasz az S betűn úgy, hogy a fölső végpontja szép lassan a szimmetriaközéppontba halad, míg a másik végpont is végig az S betűn marad (a hossza végig 1 egység) és végül eléri az S betű alját. Milyen utat jár be az F?
|
|
|
| [1389] HoA | 2010-03-14 10:17:54 |
 A "Majd tökölgetek milliméter-papírral és egy körzővel" mondatból arra következtetek, hogy barátunk nem abban tévedett, hogy a kör legtávolabbi pontja van 22 cm-re, hanem abban, hogy a húr hossza 395 cm. Nem hinném, hogy 4 méteres milliméterpapíron dolgozna. Ezért inkább azt hiszem, a húr csak 395 mm és akkor a legtávolabbi kör-pont lehet 22 cm = 220 mm-re, hiszen az több, mint 197,5 mm. Az általad leírt megoldás menete természetesen ekkor is helyes, csak a számszerű eredmények lesznek mások.
|
| Előzmény: [1386] SmallPotato, 2010-03-07 23:37:22 |
|
|
| [1387] Tudorabb | 2010-03-08 03:23:07 |
 Ez igen! Egy valóban kapkodó kérdésből kibogarászni a tényleges kérdést is tudást igényel. A 22 cm jelentőségét valamilyen oknál fogva figyelmen kívül hagytam, így az Attilát is félrevezettem, amit nagyon sajnálok. Válaszod tökéletesen érthető és nagyon köszönöm.
Üdv. Péter
|
| Előzmény: [1386] SmallPotato, 2010-03-07 23:37:22 |
|
| [1386] SmallPotato | 2010-03-07 23:37:22 |
 Ha jól értelek, van egy kör, amelynek egy húrja 395 cm hosszú. Ez, mint Attila is írta, természetesen önmagában kevés a húrhoz tartozó középponti szög meghatározásához. (Ha belegondolsz, a kör átmérője lehetne épp 395 cm, ekkor a szög 180°, vagy mondjuk 2*395 cm, ekkor a szög 60° stb.)
Ha jól értelmezem a mondatodat, akkor a jelzett húr és a hozzá tartozó rövidebb körív felezőpontja közötti távolság 22 cm. Ekkor először kiszámíthatod a kör sugarát, abból szögfüggvénnyel a húrhoz tartozó középponti szöget és abból az ív hosszát. (Amit írsz, hogy a kör legtávolabbi pontja lenne 22 cm-re, az lehetetlen, hisz a legtávolabbi pont a kör középpontjának túloldalán van, de a kör sugara már önmagában minimum  cm kell hogy legyen.) cm kell hogy legyen.)
A húr felére, a húr felezőpontját a körközépponttal összekötő szakaszra és a húr végpontjából induló sugárra felírt Pitagorasz-tétellel  ahonnan R=897,51 cm; innen a középponti szög ahonnan R=897,51 cm; innen a középponti szög  fok, amivel az ív fok, amivel az ív  cm. cm.
|
| Előzmény: [1385] Tudorabb, 2010-03-07 17:42:32 |
|
| [1385] Tudorabb | 2010-03-07 17:42:32 |
 Kedves Attila! Amennyiben az 1383-as kérdésre válaszoltál is köszönöm szépen a segíteni akarásodat. Majd tökölgetek milliméter-papírral és egy körzővel. Apropó. Ha ez még segítene. A két pontot összekötő egyenes és a kör legtávolabbi pontja közti távolság ca. 22cm.
Minden jót kívánok, Péter
|
|
|
| [1383] Tudorabb | 2010-03-07 16:09:52 |
 Üdvözöllek Benneteket! Harmincöt éve érettségiztem és a jelek szerint sokat felejtettem. Kérdéseiteket és az arra adott válaszokat olvasgatva arra következtettem, hogy a legjobb helyen járok - Nálatok. Kérdés: A körből kivágok egy cikket. A sugarak és a kör metszéspontjainak egy egyenessel összekötött távolsága adott.( 395 cm )Milyen hosszú az ív, ill. a sugár? A számításotok menete érdekelne.
Segítségeteket előre is köszönöm, Péter
|
|
| [1382] HoA | 2010-02-27 23:06:29 |
 Felhasználjuk, hogy ha P az ABC háromszög belsejében vagy AB oldalán ( P != A ) fekszik, akkor AP + PB < AC + CB . Legyen ugyanis az AP és BC egyenesek metszéspontja Q. Ez a BC oldal belső pontja vagy B maga. Ekkor AP + PB <= AP + PQ + QB = AQ + QB < AC + CQ + QB = AC + CB.
A feladat szerint az AC és DE húrok és ívek egyenlőek, így a hozzájuk tartozó középponti szögek is. Legyen a kör középpontja O, D tükörképe az AB átmérőre D'. D'OB =DOB =DOB >=DOE >=DOE =COA =COA Így O a CD'B háromszög belsejében vagy ( ha E = B ) CD' oldalán fekszik, a fentiek szerint tehát CB + DB = CB + BD' > CO + OD' = 1 + 1 = 2 Így O a CD'B háromszög belsejében vagy ( ha E = B ) CD' oldalán fekszik, a fentiek szerint tehát CB + DB = CB + BD' > CO + OD' = 1 + 1 = 2
- Vegyük észre, hogy EB nélkül is teljesül az egyenlőtlenség!
- Egyenlőséget abban az elfajuló esetben kapunk, ha C = A és D = E = B
|
| Előzmény: [1375] m.atekoos, 2010-02-27 11:21:57 |
|
|
|
|
|
| [1377] Radián | 2010-02-27 19:10:36 |
 PC szakasszal mesd el az AB-t a kapott pont legyen Q. A CQ nem lehet egyszerre nagyobb AC és BC szakasznál is, mivel ha nem így lenne (felhasználva, hogy nagyobb oldallal szemben nagyobb szög van), akkor CAB szög> AQC szög és CBA>CQB szög egyszerre teljesülne,így CAB szög+CBAszög>AQC szög+CBQ szög=180 fok ez lehetetlen. Így kaptuk: PC<QC<CA v. CB <AB<PA+PB
|
| Előzmény: [1376] m.atekoos, 2010-02-27 15:23:16 |
|
| [1376] m.atekoos | 2010-02-27 15:23:16 |
 Itt egy feladat ami egy eszméletlen egyszerű de nekem sehogy se sikerült Segítene vki?
Tetszőleges 3szög belsejében felvesszük tetszőleges p pontot. Biz be, h a 3szög összes belső pontjára teljesül: AP+PB>PC Ilyenkor AB a leghosszabb oldal(ak egyike).
Előre is köszi a segítséget.
|
|
| [1375] m.atekoos | 2010-02-27 11:21:57 |
 Tudnátok segíteni?
Itt a feladat: egy egységnyi sugarú kör kerületére felvesszük ilyen sorrendben: A C D E B úgy hogy AB átmérő, tehát C,D,E egy félköríven helyezkedik el. Tudjuk hogy AC=DE. Biz be hogy CB+DB+EB>=2.
|
|
| [1374] sakkmath | 2010-02-25 10:40:53 |
 Kiegészítés a 162. feladathoz:
Nincs szükség számítógépes programra akkor, ha csak t1 = t2 bebizonyítására szorítkozunk és lemondunk a bonyolult területarány-képlet igazolásáról. Legyen ez a leszűkítés a 162/a feladat.
|
| Előzmény: [1355] sakkmath, 2010-01-06 16:51:48 |
|
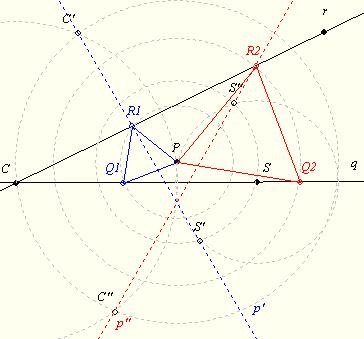
| [1373] BohnerGéza | 2010-02-20 19:06:11 |
 Egy kicsit bővebb segítség:
A feladat a szerkesztések egyik alapgondolatát tartalmazza:
Adott két pont számára egy-egy vonal (egyenes vagy kör esetleg kúpszelet) és ismerünk egy geometriai leképezést, mely az első pontot a másodikba viszi.
Ekkor az első pont számára meglévő vonalra alkalmazva a leképezést, annak képe újabb vonal a második pont számára. A második már ismert pontra a leképezés inverzét alkalmazva, megkapjuk az első pontot.
A mostani feladat szerkesztésénél figyelni kell, hogy két irányba forgathatunk! Az ábrán a q egyenes képeit a C és az S pontforgatásával kaptuk. A q'=C'S' a -60, a r"=C"S" a +60 fokos forgatás eredménye.
Amennyiben a qr szög 60 fok, ahogy a feladat feltétele mondja, akkor a q" párhuzamos lesz r-rel és csak egy megoldást kapunk. (A szerkesztés szempontjából mindegy, hogy P a szögfelezőn van vagy sem.)
|
 |
| Előzmény: [1369] laci777, 2010-02-20 14:00:57 |
|
|
| [1371] laci777 | 2010-02-20 14:53:13 |
 Köszönöm szépen - így leírva egyszerűnek tűnik. De nem állítanám, hogy térlátás nélkül evidens számomra a szögszár P pont körül elforgatása:(
Még egyszer köszönöm, kellemes hétvégét, szia: Laci
|
| Előzmény: [1370] jenei.attila, 2010-02-20 14:38:03 |
|
| [1370] jenei.attila | 2010-02-20 14:38:03 |
 Legyen A és B a háromszög másik két csúcsa, amelyek az egyik illetve másik szögszárra esnek. Mivel a háromszög szabályos, ezért az A-t a B-be egy 60 fokos P középpontú forgatás viszi. Tehát forgasd el P körül az egyik szögszárat 60 fokkal, és ahol az elfogatott szögszár elmetszi a másik szögszárat, ott lesz az egyik keresett csúcs. Ezt visszaforgatva, megkapod a másik csúcsot.
|
| Előzmény: [1369] laci777, 2010-02-20 14:00:57 |
|
| [1369] laci777 | 2010-02-20 14:00:57 |
 Sziasztok!
Tudna valaki segíteni?
Egy geometria szorgalmi feladattal gyűlt meg a bajom:
Vegyünk egy 60 fokos szöget, és a szögszáron belül egy tetszőleges P pontot, ahogy a P nem illeszkedik a 60 fokos szöget felező félegyenesre.
A feladat: szerkesszünk olyan szabályos 3-szöget, amelynek a P pont az egyik csúcsa, a másik két csúcs pedig a 2 szögszáron található (száranként 1-1).
Bármilyen segítséget előre is köszönök szépen.
Kellemes hétvégét kívánok mindenkinek!
Sziasztok: Laci
|
|
| [1368] HoA | 2010-01-14 11:45:29 |
 Elnézést, én sem gondoltam egészen végig. A 3 adott kör közül kettőnek az érintési pontjára vonatkozó inverzió igen egyszerű megoldást ad: két párhuzamos egyenest és egy kört érintő kört kell szerkeszteni. A gyakorlati kivitelezés különösen egyszerű, ha a k1 és k2 érintési pontja mint középpont körül az inverzió alapkörét úgy vesszük fel, hogy merőlegesen metssze k3-at. Ekkor k3 képe önmaga, és így a k3-at és az őt érintő két párhuzamost érintő kört kell szerkeszteni.
|
| Előzmény: [1363] S.Ákos, 2010-01-13 11:47:39 |
|
|
|
|
| [1364] HoA | 2010-01-13 12:06:17 |
 Az apró trükk ott van, hogy a legegyszerűbb megoldás nem használja ki, hogy a körök érintik egymást: Csökkentsük a körök sugarát a legkisebbik - legyen k3 - sugarával, ekkor a szerkesztendő k4 körrel koncentrikus k5 kört kell szerkeszteni, ami a csökkentett sugarú k1' és k2' köröket érinti és átmegy az O3 ponton. Az O3 középpontú inverzióval ez két kör közös érintőjének szerkesztésébe megy át. A Geometriai feladatok gyűjteményében a két kört kívülről érintő, adott P ponton áthaladó kör szerkesztésére szerepel egy inverziót nem használó módszer. Ott a körök külső hasonlósági pontját P-vel összekötő egyenesnek azt a Q pontját határozzuk meg először, amely szintén rajta van a szerkesztendő körön és így visszavezetjük a feladatot a két ponton átmenő, adott kört érintő kör szerkesztésére.
|
| Előzmény: [1362] Bosnyak, 2010-01-13 09:55:25 |
|
|
| [1362] Bosnyak | 2010-01-13 09:55:25 |
 Üdv mindenkinek! Volna egy problémám: Van három különböző tetszőleges sugarú kör ami érinti egymást. Annak a körnek a középpontját szeretném megszerkeszteni amely mind a három másik kört érinti,(belülről, a három kör által határolt területen) Remélem tud vki segíteni!
|
|
|
|
|
| [1358] BohnerGéza | 2010-01-10 15:27:53 |
 Az alábbi feladat felhasználható az OKTV - 2009-9010. II. kategória 3. feladatánál, de önmagában is jó feladat.
Használjuk ki a tg fv. tulajdonságait!
|
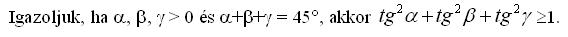 |
|
|
|
| [1355] sakkmath | 2010-01-06 16:51:48 |
 A következő feladatomat ajánlom megoldásra. (A megoldás végén valószínűleg elkerülhetetlen lesz számítógépes program használata. Ha ezért kissé kilógna e topicból, elnézést ... .)
(Kb.) 162. feladat: Egy hegyesszögű, nem egyenlő szárú háromszög területe T, oldalainak hossza a, b és c. A háromszög valamennyi magassági talppontján át húzzunk párhuzamost a talpponti oldallal szemközti csúcs szögfelezőjével. Tekintsük az így kapott egyeneseknek a szögfelező egyenesekkel alkotott metszéspontjait. Bizonyítsuk be, hogy e pontok két egyenlő területű háromszöget határoznak meg, melyek t1, illetve t2 nagyságú területére:
|
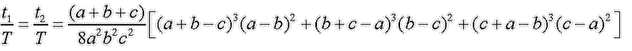 |
|
|
| [1353] laci777 | 2010-01-05 22:59:40 |
 Hát igen... Nekem meg épp ez a feladat volt elsőre (meg másodikra is...:P) megoldhatatlan.
Azért szerintem a túlzott szerénységre nincs okod:)
Köszönöm és további szép estét: Laci
|
| Előzmény: [1352] SmallPotato, 2010-01-05 22:47:32 |
|
|
|
| [1350] laci777 | 2010-01-05 22:43:06 |
 Kedves SmallPotato!
Nagyon szépen köszönöm az elegáns megoldást - bár lehet, itt ez a példa nem lehetett komolyabb kihívás.
Nem vettem észre a hasonló háromszögeket (sem)...
Még egyszer köszönöm!
További szép estét, szia: Laci
|
| Előzmény: [1348] SmallPotato, 2010-01-05 22:15:41 |
|
| [1349] HoA | 2010-01-05 22:31:51 |
 Ja, az más. Ha biztosra akarsz menni, használd [1343] lépéseit. Vagy kérdezd meg [1341] szerzőjét, ő hogy jutott erre az eredményre.
|
| Előzmény: [1346] Tym0, 2010-01-05 21:17:10 |
|
|
| [1347] SmallPotato | 2010-01-05 22:09:51 |
 Rajzold fel az elrendezésnek a kúp tengelyén átmenő síkmetszetét. Rajzold be a gömb két sugarát: a kúp alapkörének középpontjába irányulót és az alkotóra merőlegest. Az ábrádon két hasonló derékszögű háromszög lesz: az egyiknek a befogói a kúp alapkörének sugara és a kúp magassága, a másiknak a befogói az alkotóra merőlegesen berajzolt gömbsugár és az alkotónak a kúp csúcsa felé eső szelete. Írd fel a befogók arányát mindkét háromszögben.
|
| Előzmény: [1342] laci777, 2010-01-05 19:41:20 |
|
| [1346] Tym0 | 2010-01-05 21:17:10 |
 Bocs de nekem nincs se időm se türelmem bizonyítani. Én biztosra akarok menni. Elkezdtem csinálni. egyébként mástól kaptam. Remélem jó lesz.
|
| Előzmény: [1345] HoA, 2010-01-05 21:15:15 |
|
