|
| [1949] Sinobi | 2022-01-20 17:35:41 |
 Szerintem ezt a kérdést megválaszoltam [1940]-ben, mekkorák az A és B-beli szögek.
A B-beli szög 64.34, az
A-beli szög 51.32.
Az ábrádat nem látom jól, de ha a 0 fok van jobb oldalt, és az alsó kör óramutatóval megegyezően, a felső pedig ellentétesen van számozva (???), akkor a metszéspontok az alsó körön
270 +- A-beli szög = 270 +- 51.32 = 321.32 és 218.68,
míg a felső körön
90 +- B-beli szög = 90 +- 64.34 = 154.34 és 25.66.
|
| Előzmény: [1947] HappyEffendi, 2022-01-19 20:34:48 |
|
| [1948] HappyEffendi | 2022-01-19 22:54:38 |
 Amint 1943-as hsz-ben jeleztem közreadnám a következő feladatot:
Adott egy 'r' sugarú kör, és annak ívén levő középponttal 6 db 'gyök(3)*r/2' sugarú kör.
Mekkora a 12 fehér köríves vonallal határolt alakzat területe?
|
 |
|
| [1947] HappyEffendi | 2022-01-19 20:34:48 |
 Kedves Erzsébet!
Köszönöm, hogy foglalkozol a témával!
Megpróbálom még szakszerűbben leírni a feladatot:
Adott két kör. A nagyobbik sugara 'r', a kisebbiké 'gyök(3)*r/2'. A kisebbik kör középpontja a nagyobbik 270. fokán van. 1943-as hozzászólás ábrája szerint.
A feladat: középpontjaiktól számítva egy-egy teljes körív mentén, hány foknál vannak a metszéspontjaik?
|
| Előzmény: [1946] Berko Erzsebet, 2022-01-17 16:58:15 |
|
| [1946] Berko Erzsebet | 2022-01-17 16:58:15 |
 Sajnos a pontos feladatot nem írtad. Adott két kör. Ha a metszéspontot összekötöm a körök középpontjával, akkor a szög: 64,34 fok. VAGY Két görbe hajlásszöge: metszéspontban húzott érintők által bezárt szög. Ez is 64,34 fok.
|
| Előzmény: [1945] HappyEffendi, 2022-01-16 23:46:29 |
|
|
|
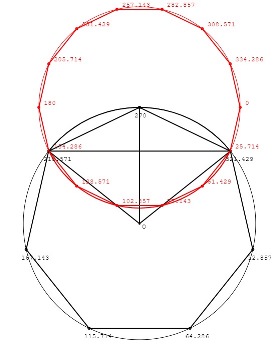
| [1943] HappyEffendi | 2022-01-06 14:41:58 |
 Kedves Sinobi!
Boldog Újévet Kívánok (természetesen mindenki másnak is)!
Sejtettem, hogy szakszerűtlen lesz a feladat leírása, de a segítségeddel mégis sikerült elindulnom a megoldás felé, főleg, miután rájöttem, hol keressem az egyenlőszárú háromszöget. :)
Az alap kérdésem az lett volna, hogy egy-egy körnek hányadik fokainál vannak a másik körrel való metszéspontjai?
Szerkesztés közben arra is rájöttem, hogy a két kör metszéspontjai egy, a nagy körbe írható szabályos hétszög, és egy, a kis körbe írható szabályos tizennégy-szög egy-egy csúcsánál vannak.
Gondolom, a geometriában képzettek ezt kapásból tudtják.
A metszéspontok e szerint:
a kis körnél 25,714 és 154,286 fok,
a nagy körnél 218,571 és 321,429 fok,
az alábbi ábra szerint.
A fenti kérdés egy összetettebb feladat része volt, amivel, ha sikerül ábrázolnom, ismét jelentkezem.
Köszönöm segítségeteket!
|
 |
| Előzmény: [1941] Sinobi, 2021-12-31 10:11:02 |
|
| [1942] Berko Erzsebet | 2022-01-02 08:13:12 |
 Szerintem először le kellene írni a feladatot, vagyis pontosítani kellene. Metszéspontok szöge? Mivel ez számomra nem világos, én pl. a két érintő szögére gondoltam.
Két metsző kör szögén a metszéspontban meghúzott körérintők szögét értjük.
|
|
| [1941] Sinobi | 2021-12-31 10:11:02 |
 Mármint a szög arccos( (piros/2) / kék ), ahol a piros gyök(3)/2, a kék pedig 1.
|
|
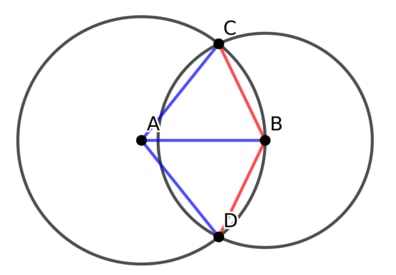
| [1940] Sinobi | 2021-12-31 10:02:11 |
 Úgy értelmeztem a kérdésedet, hogy a körívek által bezárt szögre vagy kíváncsi (ábrán az ABC háromszög C-ben levő szöge). Most inkább úgy hiszem, hogy az ábrán az ABC háromszögben A-ban, illetve B-ben levő szögekre (vagy azok duplájára) vagy kíváncsi.
Akárhogy is, a háromszög oldalai (r, r, sqrt(3)/2 r), aminek az alapon fekvő szögei (C és B-beli szögek) arcos( kék/ (piros/2) ) = arccos( gyök(3) / 2 / 2), az A-beli szöge meg 180-2*arccos( gyök(3) / 4)).
|
 |
| Előzmény: [1939] HappyEffendi, 2021-12-30 20:31:56 |
|
|
| [1938] Sinobi | 2021-12-30 15:21:39 |
 Körök szöge az ugyanaz, mint a metszéspontba húzott sugarak szöge.
Ha felveszed a középpontokat és a metszéspontba húzott sugarakat, akkor egy (r,r,gyök(3)/2 r) egyenlőszárú háromszöget kapsz, és ennek a szögeire vagy kíváncsi.
|
| Előzmény: [1936] HappyEffendi, 2021-12-27 23:49:47 |
|
| [1937] HappyEffendi | 2021-12-28 00:14:23 |
 Elnézést, az ábra lemaradt, de talán nincs is rá szükség!
|
 |
|
| [1936] HappyEffendi | 2021-12-27 23:49:47 |
 Kedves Fórumozók!
Segítséget kérnék, mivel nem vagyok járatos a matematika és geometria világában:
Adott két egymást metsző kör. Az egyik r, a másik négyzetgyök(3) * r / 2 sugarú. A nagyobbik kör érinti a kisebbik középpontját.
Kérdésem: mi a képlet a metszéspontok szögeinek meghatározásához?
JavaScript-ben rajzoltam meg canvas-on, szemre többé-kevésbé jól kidekáztam az értékeket, de jó lenne, ha a gép pontosan kiszámolná. A teljesség kedvéért ideírom a körívrajzolás kódját:
ctx.arc(x, y, r, (Math.PI / 180) * 218.65, (Math.PI / 180) * 321.35);// nagy kör íve, ctx.arc(x, y, Math.sqrt(3) * r / 2, (Math.PI / 180) * 25.65, (Math.PI / 180) * 154.35);// kis kör íve, az óramutató járása szerint.
Bocsánat a valószínűleg szakszerűtlen feladatleírásért és előre is köszönök minden segítséget!
|
|
|
| [1934] Erben Péter | 2021-06-07 14:39:58 |
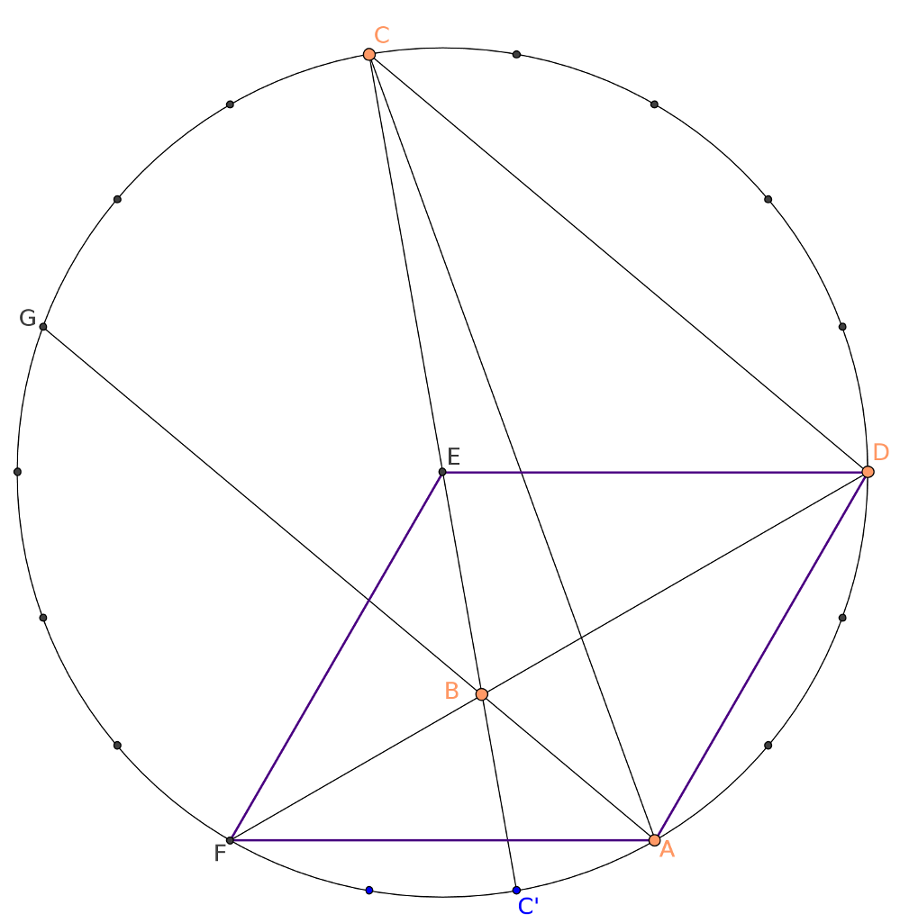
 A feladat egy lehetseges eredete a szabalyos 18-szog atloinak az a tulajdonsaga, hogy egymassal bezart szoguk mindig a 10 fok egesz tobbszorose.
Ha \(\displaystyle C\), \(\displaystyle D\) es \(\displaystyle A\) egy szabalyos 18-szog megfelelo csucsai, akkor \(\displaystyle E\) eppen a sokszog kozeppontja.
A kozbulso lepes, hogy a \(\displaystyle CC'\), \(\displaystyle AG\) es \(\displaystyle DF\) atlok egy ponton mennek at, ami peldaul visszavezetheto arra, hogy \(\displaystyle EDAF\) egy rombusz, amelynek szogei 120 fok es 60 fok.
Mindez persze nem a feladat megoldasa, inkabb azt mutatja, hogyan "keszulhetett" a kerdes.
|
 |
| Előzmény: [1933] Lpont, 2021-06-07 12:32:53 |
|
| [1933] Lpont | 2021-06-07 12:32:53 |
 I. Szögszámolással adódik, hogy BD felezi az ABCD négyszög B-nél levő szögét.
II. A-t tükrözve BD-re a kapott E pont rajta van BC egyenesén és AD=ED.
III. Újabb szögszámolás után EDC háromszög egyenlő szárú, ED=EC.
IV. Harmadjára is szögeket számolva EC=EA, tehát AE=EC=ED=AD, azaz AED háromszög szabályos, minden szöge 6alfa, így alfa=10fok.
|
| Előzmény: [1932] rezes, 2021-06-06 13:18:23 |
|
| [1932] rezes | 2021-06-06 13:18:23 |
 \(\displaystyle ABCD\) konvex négyszögben \(\displaystyle BC=CD, BAC\sphericalangle=3\alpha\), \(\displaystyle BCA\sphericalangle=\alpha,\) \(\displaystyle ACD\sphericalangle=3\alpha\), \(\displaystyle DAC\sphericalangle=5\alpha.\) Mennyi \(\displaystyle \alpha\) értéke?
|
|
| [1931] HoA | 2021-02-03 12:52:03 |
 Bocsánat, elírás. Helyesen:
A \(\displaystyle D_0D_1F_1\) és \(\displaystyle D_0D_2F_2\) háromszögek hasonlók, \(\displaystyle D_0, F_1 és F_2\) egy egyenesen vannak.
|
| Előzmény: [1930] HoA, 2021-02-03 12:34:31 |
|
| [1930] HoA | 2021-02-03 12:34:31 |
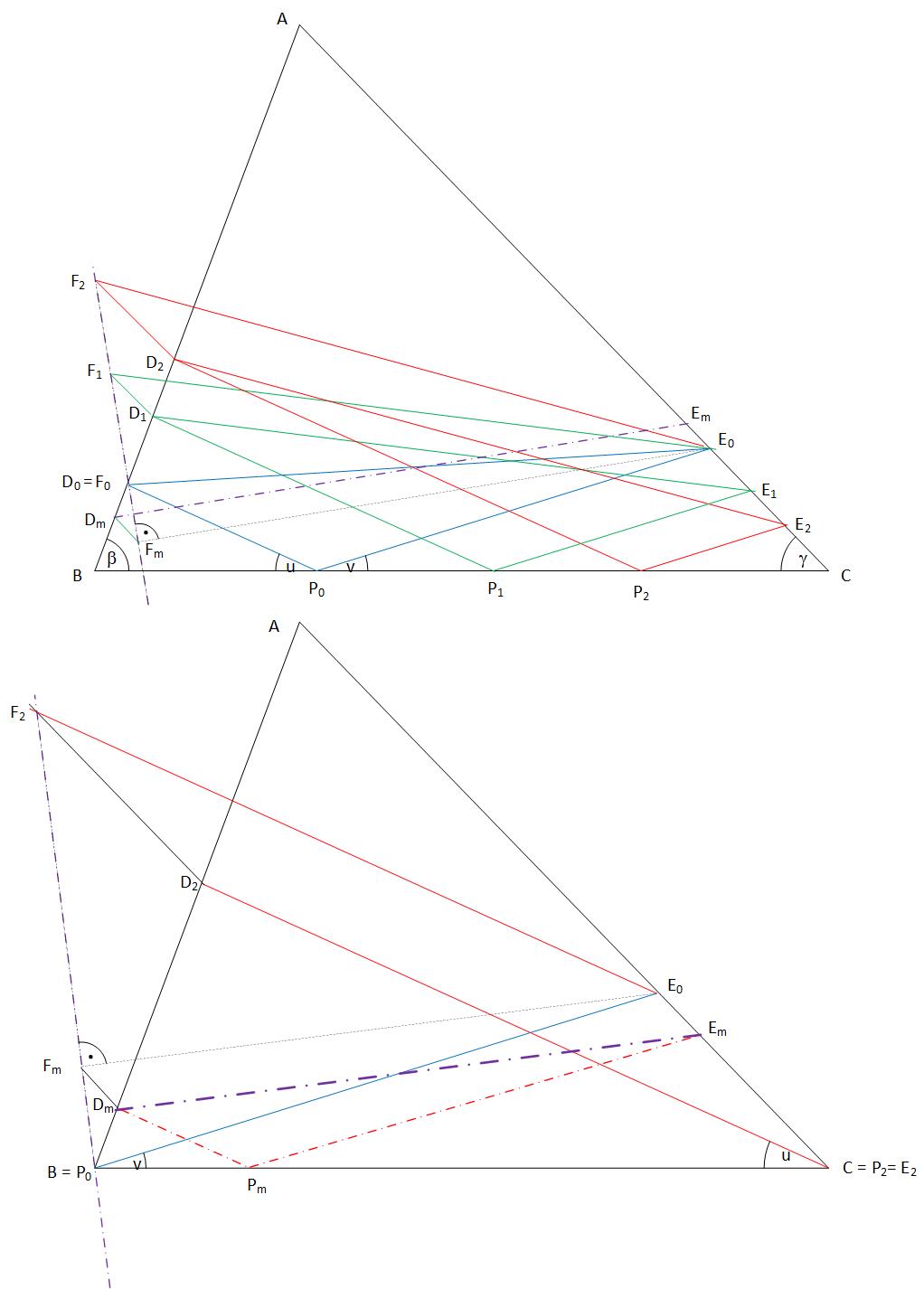
 Legyen \(\displaystyle P\) egyik helyzete \(\displaystyle P_0\). Rajzoljuk meg az ehhez tartozó \(\displaystyle P_0D_0\) és \(\displaystyle P_0E_0\) szakaszokat. P egy másik, \(\displaystyle P_1\) helyzetéhez tartozzanak A \(\displaystyle D_1\) és \(\displaystyle E_1\) pontok. A párhuzamos szelők tétele szerint \(\displaystyle BP_0 D_0\) háromszögből \(\displaystyle D_0D_1 = k P_0P_1\) , ahol \(\displaystyle k = \frac{sin u}{sin(\beta + u)}\) . Hasonlóan a \(\displaystyle P_0CE_0\) háromszögből \(\displaystyle E_0E_1 = m P_0P_1\) , ahol \(\displaystyle m = \frac{sin v}{sin(\gamma + v)}\) . Toljuk el \(\displaystyle E_1D_1\) -et önmagával párhuzamosan az \(\displaystyle AC\) egyenes mentén úgy, hogy \(\displaystyle E_1\) \(\displaystyle E_0\) -ba kerüljön. \(\displaystyle D_1\) új helyzete legyen \(\displaystyle F_1\) . \(\displaystyle D_1E_1E_0F_1\) paralelogramma, \(\displaystyle D_1F_1 \# E_1E_0\) , \(\displaystyle \frac{D_0D_1}{D_1F_1} = \frac {k}{m}\). Ismételjük meg egy további \(\displaystyle P_2\) pontra a \(\displaystyle P_1\) -re elvégzetteket. Kapjuk a \(\displaystyle D_2 , E_2, F_2\) pontokat. \(\displaystyle \frac{D_0D_2}{D_2F_2} = \frac {k}{m}\). A \(\displaystyle D_0D_1F_1\) és \(\displaystyle D_0D_2F_2\) háromszögek hasonlók, \(\displaystyle D_0, D_1 és D_2\) egy egyenesen vannak. A megfelelő \(\displaystyle D_iE_i\) szakasszal párhuzamos és azonos hosszúságú \(\displaystyle F_iE_0\) szakaszok egyik végpontja közös (\(\displaystyle E_0\)) , a másik az \(\displaystyle F_iF_j\) egyenesen mozog. Közülük a legrövidebb az \(\displaystyle E_0\) -ból az \(\displaystyle F_iF_j\) -re bocsátott merőleges \(\displaystyle F_m\) talppontját \(\displaystyle E_0\) -lal összekötő szaksz lesz. A keresett legrövidebb \(\displaystyle DE\) szakaszt akkor kapjuk, ha \(\displaystyle E_0F_m\) -et az \(\displaystyle AC\) egyenes mentén úgy toljuk el, hogy \(\displaystyle F_m\) az \(\displaystyle AB\) egyenesre essék, a szakasz végpontjai legyenek \(\displaystyle D_m és E_m\)
A szerkesztést úgy hajthatjuk végre a legkevesebb vonal megrajzolásával, ha P két szélső helyzetét használjuk. Legyen tehát \(\displaystyle P_0 = B, P_2=C\) , \(\displaystyle E_0\) az \(\displaystyle AC\) oldalnak az a pontja, melyre \(\displaystyle E_0BC \angle = v\) , \(\displaystyle D_2\) az \(\displaystyle AB\) oldalnak az a pontja, melyre \(\displaystyle D_2CB \angle =u\) . \(\displaystyle CD_2\) -t \(\displaystyle CA\) mentén úgy eltolva, hogy \(\displaystyle C\) \(\displaystyle E_0\) -ba jusson \(\displaystyle D_2\) kerüljün \(\displaystyle F_2\) -be .\(\displaystyle E_0\) -ból az \(\displaystyle F_2B\) egyenesre bocsátott merőleges talppontja legyen \(\displaystyle F_m\) . A legrövidebb DE szakaszt \(\displaystyle E_0F_m\) -nek \(\displaystyle AC\) -vel párhuzamos eltolásával kapjuk úgy, hogy \(\displaystyle F_m\) az \(\displaystyle AB\) egyenesen lévő \(\displaystyle D_m\) -be kerüljön, \(\displaystyle E_0\) pedig \(\displaystyle E_m\) -be.
Ujjgyakorlatnak hagyjuk annak bizonyítását, hogy a \(\displaystyle D_m\) -ből \(\displaystyle D_2C\) -vel húzott párhuzamos és az \(\displaystyle E_m\) -ből \(\displaystyle E_0B\) vel húzott párhuzamos egy, a \(\displaystyle BC\) egyenesen fekvő, feladatunk megoldását adó \(\displaystyle P_m\) pontban metszik egymást.
|
 |
| Előzmény: [1929] sakkmath, 2021-01-21 23:58:57 |
|
| [1929] sakkmath | 2021-01-21 23:58:57 |
 A 192. feladat valóban nyitott. Talán ezért (is) nagyon nehéz, de megoldható. Az általam ismert megoldást nyolc éve publikálták, azóta a közlés helyén, egy közismert, frekventált oldalon, állócsillagként ragyog: még nem reagált rá senki – legalábbis ott nem. Ebből arra következtetek, hogy máig csak ez az egy megoldás létezik. Ez a dolgozat – a szerkesztéses részét tekintve – mindvégig euklideszi szerkesztésekkel jut el a \(\displaystyle P\) pont keresett pozíciójához.
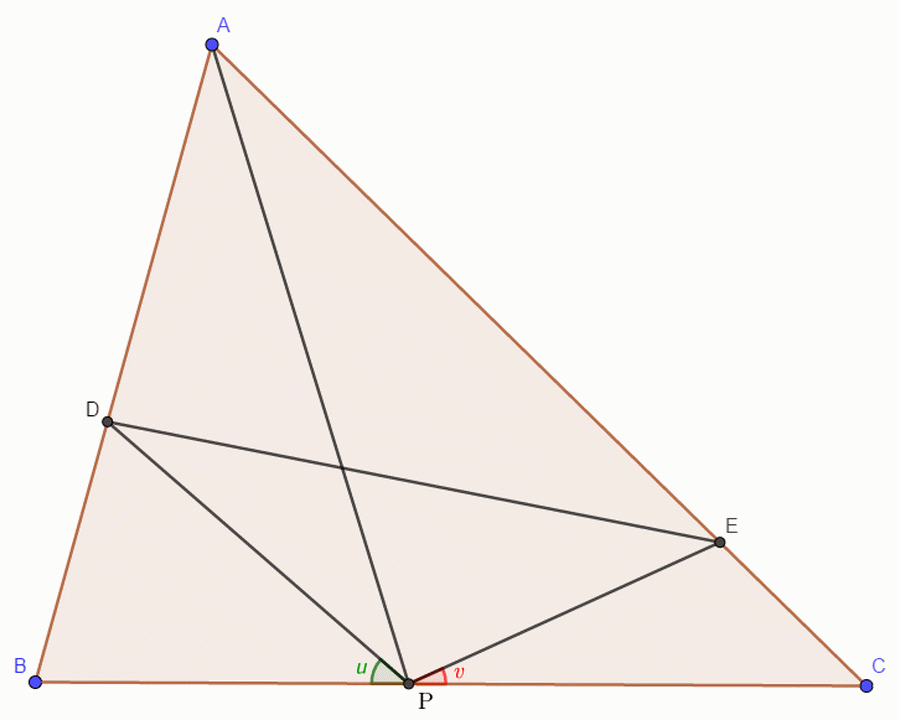
Beírom a lényegesen könnyebb,193. feladatot is, amely csak u és v szerepét tekintve különbözik a rokon 192.-től. Találjunk euklideszi szerkesztést alkalmazó megoldást a következő, 193. feladatra:
Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalán mozog egy \(\displaystyle P\) pont. Az \(\displaystyle AB\) oldal \(\displaystyle D\), valamint az \(\displaystyle AC\) oldal \(\displaystyle E\) pontjára fennáll, hogy rögzített e két szög: \(\displaystyle u=BPD∠\) és \(\displaystyle v=CPE∠\). Keressük meg a \(\displaystyle P\) pont azon helyzetét, amelyre a \(\displaystyle DE\) szakasz hossza minimális!
|
 |
| Előzmény: [1928] Sinobi, 2021-01-19 18:24:05 |
|
| [1928] Sinobi | 2021-01-19 18:24:05 |
 Nagyon nyitott a feladat, és nekem kételyeim is vannak azzal kapcsolatban, hogy van értelmes, szép válasz. Az ennél egyszerűbbnek tűnő
Philo szelő probléma: adott egy szög és benne egy pont, keressük meg a legrövidebb szakaszt, amely átmegy a ponton, és a végpontjai a szög két szárán van
sem szerkeszthető már körzővel és vonalzóval. Bár az például megoldható olyan eszközzel, amelyik megadja két kúpszelet metszéspontjait.
|
|
| [1927] sakkmath | 2021-01-13 23:43:55 |
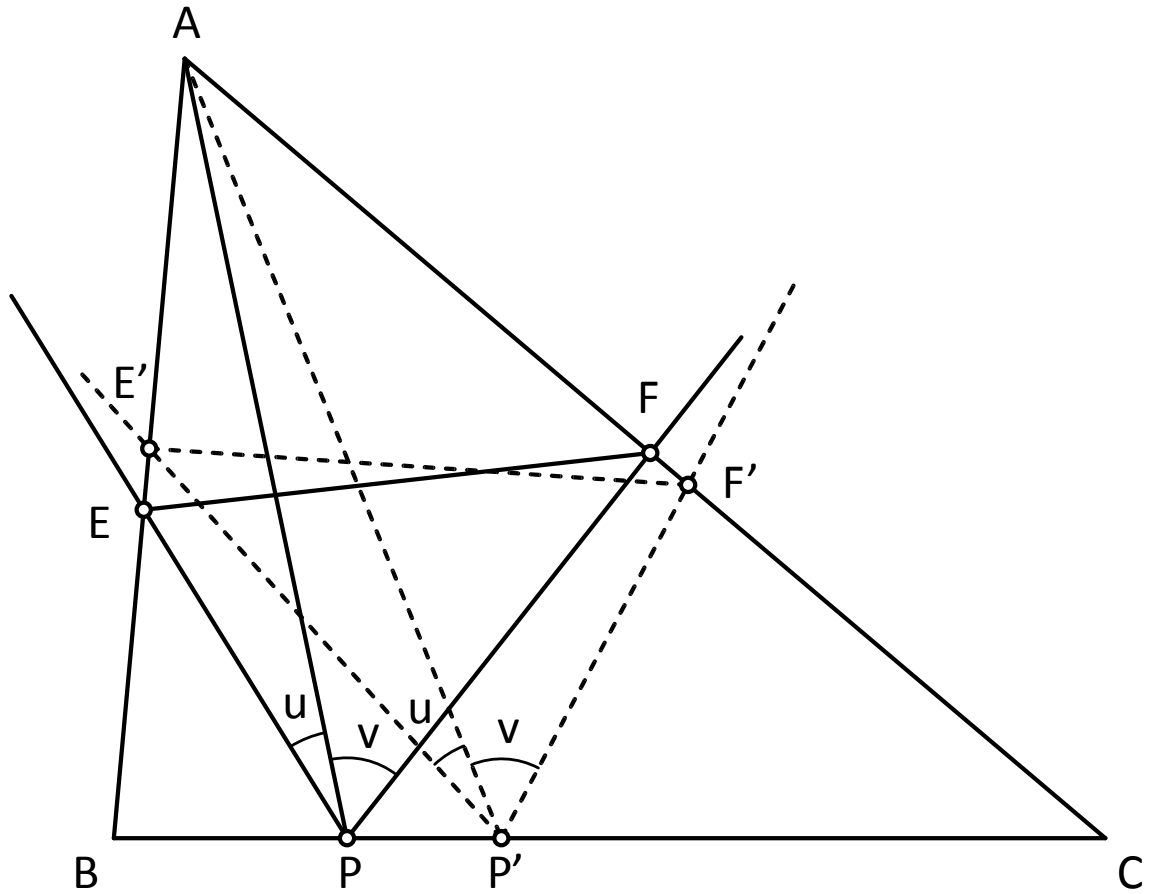
 \(\displaystyle {\bf 192.}\) \(\displaystyle {\bf feladat}\): Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalán mozog egy \(\displaystyle P\) pont. Az \(\displaystyle AB\) oldal \(\displaystyle E\), valamint az \(\displaystyle AC\) oldal \(\displaystyle F\) pontjára fennáll, hogy konstans az \(\displaystyle u = EPA\angle\) és a \(\displaystyle v = APF\angle\). Keressük meg a \(\displaystyle P\) pont azon helyzetét, amelyre az \(\displaystyle EF\) szakasz hossza minimális!
|
 |
|
| [1926] HoA | 2019-12-06 14:58:36 |
 Mit nevezzünk helytállónak? A módszer körívekből állít össze egy, az ellipszist közelítő görbét. Megvizsgálhatjuk például, a megfelelő tengelyeket egymásra fektetve a tengelyek hosszának függvényében a nagytengely pontjait abszcisszáknak, az ellipszis ill. a közelítő görbe hozzárendelt pontjait ordinátáknak tekintve, mennyi az ordináták eltérésének maximuma. Vagy mekkora a két görbe közötti területdarabok "vastagsága" . Te mire gondoltál ?
|
| Előzmény: [1925] TTibi, 2019-12-04 16:55:34 |
|
|
| [1924] Sinobi | 2017-05-21 13:05:29 |
 Adott egy kör, és rajta kívül két pont. A pontokból érintőket húzunk a körhöz. Igazold, hogy a négy érintési pont a két ponttal egy kúpszeletre esik. Igazold továbbá, hogy ennek a kúpszelet egy pontjából ha a körhöz húzunk érintőt, és így csináljuk a Poncelet tételben szereplő eljárást, akkor 4 lépés után záródik.
(könnyű)
|
|
| [1923] Vonka Vilmos Úr | 2017-04-26 13:40:54 |
 A fókuszok valós eszközökkel is szépen kezelhetőek: kúpszelet fókusza olyan pont, amelyre illeszkedő konjugált egyenespárok pontosan a merőleges egyenespárok.
Komplex módszerekkel is meg lehet őket fogni: az abszolút képzetes körpontokból érintőket húzunk a kúpszelethez, ezek páronként vett további metszéspontjai a fókuszok. Így a két valós fókusz mellett egy képzetes fókuszpár is adódik.
|
| Előzmény: [1922] Sinobi, 2017-04-26 09:42:48 |
|
| [1922] Sinobi | 2017-04-26 09:42:48 |
 Aham. A gyengébb állítás, amelyben két egyenesre kell esniük, az itt található tétel2-nek a Minkowski geometriában való felírása, az erősebb állítás, amelyben az is elég ha kúpszeletre esnek, pedig a de Sitter geometriában (ahol a szög és a távolságmérés is hiperbolikus) való kimondása.
Kúpszeletek fókuszai kezelhetők szépen egyszerűen komplex projektív módszerekkel? (ebben a két geometriában valós projektív eszközökkel is megfoghatók a fókuszpontok)
|
| Előzmény: [1921] Vonka Vilmos Úr, 2017-03-27 08:07:20 |
|
| [1921] Vonka Vilmos Úr | 2017-03-27 08:07:20 |
 Kúpszeletsorokra vonatkozó számolásokkal (amik nem túl nehezek, csak kúpszeletek egyenleteiből kell lineárisan kikombinálgatni a kúpszeletsoruk további kúpszeleteinek egyenletét) egy kicsit általánosabbat is be tudok látni:
Ha adott három kúpszelet úgy, hogy közülük bármely kettőnek két metszéspontja egy negyedik kúpszeleten van (ez most esetünkben egy metsző egyenespár), akkor a további két metszéspont-párok összekötő egyenesei konkurrensek.
De még jó lenne erre valami szebb bizonyítást keresni (szerintem algebrai görbék fokszámát vizsgálva, mint az eredeti "kalapács" esetén a Cayley-Bacharach tételes szép bizonyítás, ki kéne jönnie).
|
| Előzmény: [1920] Sinobi, 2017-03-26 16:09:26 |
|
| [1920] Sinobi | 2017-03-26 16:09:26 |
 Ha a nagy négyzetbe is ellipszist írunk, majd azt dualizáljuk, akkor az előző kalapácshoz nagyon hasonló állítást kapunk: adott két egyenesen 3-3 pont, ezeken át 3 kúpszelet úgy, hogy bármelyik 2-nek 4 metszéspontja legyen, bizonyítsuk be hogy a hatványvonalak 1 ponton mennek át.
Azt hogyan látnád be, ha nem ezt akarnád dualizálni?
(azt ebből tudjuk, hogy mint konfiguráció azonos az előbbi kalapáccsal, vagyis a PG téma 126-ik hozzászólásával, de mondjuk ez nem tűnik fel; meg nem is látom most hogy mi hova kerül)
|
| Előzmény: [1918] Vonka Vilmos Úr, 2017-03-25 17:10:09 |
|
| [1919] Sinobi | 2017-03-25 18:42:14 |
 Kalapács és szög :D Tetszik :)
|
|
| [1918] Vonka Vilmos Úr | 2017-03-25 17:10:09 |
 Na jó, ezt elismerem, hogy kicsit elkapkodtam. (Attól még, hogy a kollineáció az egyik téglalapot a másikba viszi, nem biztos, hogy a beírt kúpszeletet is éppen a tekintett másikba viszi át.)
Újabb próbálkozás:
A másik fórumban beszéltünk a következő állításról: Ha három kúpszeletnek van két közös pontja, akkor a további két-két metszéspontot összekötő egyenesek konkurrensek.
Nézzük ennek az állításnak a duálisát: Ha három kúpszeletnek van két közös érintője, akkor a további két-két közös érintők metszéspontjai kollineárisak.
Legyen most két kúpszeletünk a két beírt ellipszis. A harmadik pedig az az elfajuló másodosztályú görbe, a négyzet két oldalirányának végtelen távoli pontjából áll. A két pontból álló elfajuló másodosztályú görbe érintői a két pontra illeszkedő összes egyenes (ez a metsző egyenespár duálisa).
Erre a három görbére alkalmazva az előbb megfogalmazott duális állítást éppen a feladat állítása adódik.
|
| Előzmény: [1917] Sinobi, 2017-03-25 01:34:01 |
|
|
| [1916] Vonka Vilmos Úr | 2017-03-24 21:58:41 |
 A két befoglaló téglalapnak a négyzet oldalain levő megfelelő csúcsait összekötő egyenesek éppen a négyzet átlóján metszik egymást (ez a Papposz-tételből könnyen látható), legyen ez a közös pont \(\displaystyle C\). Ez azt jelenti, hogy \(\displaystyle C\) centrumú kollineációval át lehet vinni az egyik kis téglalapot a másikba. Ez a kollineáció az egyik téglalapba írt ellipszist a másik téglalapba írt ellipszisbe viszi. Így a közös érintők invariáns egyenesek, vagyis átmennek a \(\displaystyle C\) centrumon.
|
| Előzmény: [1914] Sinobi, 2017-03-24 18:13:28 |
|
|
| [1914] Sinobi | 2017-03-24 18:13:28 |
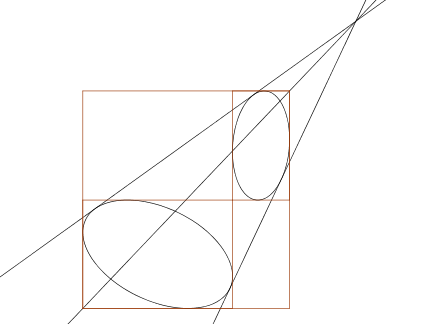
 191. Feladat Egy négyzetet felosztunk 4 részre, két szemközti részbe ellipsziseket írunk az ábra szerint. Bizonyítsd be, hogy a két ellipszis két másik közös érintőjének a metszése a négyzet átlóján van.
|
 |
|
|
| [1912] Cogito | 2016-11-25 22:57:41 |
 A feladatot 1955. január 2-án az alábbi formában adták fel az – akkor még Rákosi Mátyásról elnevezett – Országos Tanulmányi Versenyen:
Egy háromszög belsejében felvett tetszőleges ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszög területét hat részre osztják. Mekkora az adott háromszög területe, ha adva van a keletkezett 3 háromszög területe: \(\displaystyle t_1\), \(\displaystyle t_2\), \(\displaystyle t_3\) ?
Érdemes ezt az általánosított feladatot is megoldani.
|
| Előzmény: [1908] Gergely99, 2016-11-22 21:10:01 |
|
| [1911] Gergely99 | 2016-11-23 23:11:49 |
 Elnézést kérek. Későn esett le a dolog. Nem aktuális a kérdés, és nagyon szépen köszönöm a választ :)
|
|
| [1910] Gergely99 | 2016-11-23 23:03:35 |
 Ez egy lehetséges megoldás lenne, de a feladat nem írta sehol, hogy a háromszög derékszögű. Ezért nem tudtam boldogulni a feladattal. Szóval a kérdés ugyan az, csak annyival kiegészítve, hogy mi van, ha a háromszögem tetszőleges?
|
|
| [1909] jonas | 2016-11-23 14:36:41 |
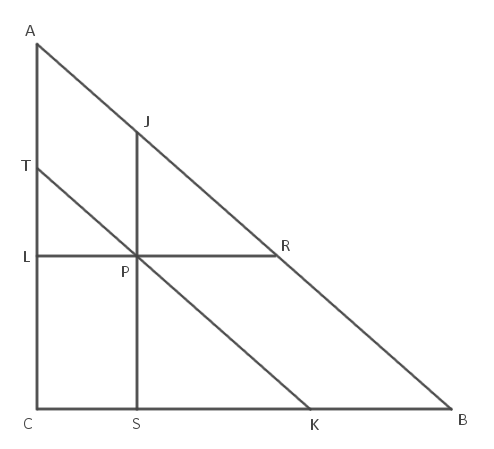
 Legyen a háromszög ABC, a belül felvett pont P. A P ponton át az AB oldallal párhuzamos a BC oldalt K-ban, az CA oldalt T-ben metszi; a BC oldallal párhuzamos az CA oldalt L-ben, az AB oldalt R-ben metszi; végül a CA oldallal párhuzamos az AB oldalt J-ben, a BC oldalt S-ben metszi.
A három kis háromszög, amiről a feladat beszél, PLT, RPJ, KSP. Vedd észre, hogy ez a három háromszög hasonló, mivel minden oldaluk párhuzamos egymással. Ráadásul a BCA háromszög is hasonló az előbbi háromhoz.
Legyen a PLT háromszög területe 1, az RPJ háromszög területe 2, a KSP háromszög területe 3. (Feltehetjük, hogy pont ilyen sorrendben vannak a területek, mert az eredeti háromszög ABC csúcsait betűzhetjük megfelelően.) Mivel az RPJ háromszög hasonló a PLT-hez, de kétszer akkora területű, ezért az oldalai \(\displaystyle \sqrt 2 \)-szer akkorák. Hasonlóan a KSP háromszög oldalai \(\displaystyle \sqrt 3 \)-szor akkorák, mint a PLT-é.
Mivel párhuzamosokat húztunk, a PJAT négyszög paralelogramma, így a TA szakasz hossza megegyezik a PJ szakasz hosszával, ez utóbbiról pedig a PLT és RPJ háromszögekből tudjuk, hogy \(\displaystyle \sqrt 2 \)-szer akkora, mint az LT szakasz. Hasonlóan PSCL is paralellogramma, így az LC ugyanolyan hosszú mint a PS szakasz, ez pedig \(\displaystyle \sqrt 3 \)-szor olyan hosszú, mint az LT szakasz.
Mármost mivel P a háromszög belső pontja, és PL párhuzamos BC-vel, ezért L a BC szakasz belső pontja. Hasonlóan PT párhuzamos AB-vel, ez pedig egy egyenesbe esik AR-rel, P pedig R és L között van, ezért T az AL szakasz belsejében van.
Ezekből az LA szakaszt a T belső pont az TA és a LT szakszra bontja, amik közül az AT-ről már megállapítottuk, hogy \(\displaystyle \sqrt 2 \)-szer olyan hosszú, mint LT, így az LA szakasz \(\displaystyle \sqrt 2 + 1 \)-szer olyan hosszú, mint LT. Hasonlóan a CA szakaszt L felbontja az LA és LC szakaszra, ezért a CA szakasz \(\displaystyle \sqrt 2 + 1 + \sqrt 3 \)-szor olyan hosszú, mint LT. Viszont a BCA háromszög hasonló a PLT háromszöghöz, és az utóbbinak a területe 1, ezért az oldalak arányából az előbbinek a területe \(\displaystyle (\sqrt2 + 1 + \sqrt3)^2 \), ami körülbelül 19.17.
|
 |
| Előzmény: [1908] Gergely99, 2016-11-22 21:10:01 |
|
| [1908] Gergely99 | 2016-11-22 21:10:01 |
 Jó estét kívánok mindenkinek!
Volna egy olyan feladatom, aminek nem tudom, hogy hogyan álljak neki, de szeretném nagyon megoldani. Pusztán kíváncsiságból szeretném megtudni, hogy hogyan kellene a feladatot megoldani.
Ez lenne a feladat:
Egy háromszög belsejében felvett ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszöget 6 részre osztják. Mekkora az eredeti háromszög területe, ha a keletkezett 3 háromszög területe: 1, 2 illetve 3 egység?
|
|
| [1907] Dömötör Erzsi | 2016-10-28 23:19:25 |
 Talán nem tartjátok OFF-nak a témát, ha nem a geometria szépségeiről írok, hanem arról, aki e fórum keretein belül olyan sok gondolatát megosztotta velünk :(
|
 |
|
| [1906] jonas | 2016-10-14 15:16:25 |
 Forgassuk el az \(\displaystyle SQ \) szakaszt derékszöggel, és toljuk el, hogy az egyik végpontja \(\displaystyle P \)-be kerüljön, így kapjuk a \(\displaystyle PT \) szakaszt. A kulcs észrevétel, hogy az \(\displaystyle RT \) egyenes megegyezik a négyzet \(\displaystyle CD \) oldalegyenesével. A másik három oldalegyenest úgy kapjuk, hogy \(\displaystyle P \)-n át párhuzamost húzunk \(\displaystyle RT \)-vel, majd \(\displaystyle Q \)-n és \(\displaystyle S \)-en át merőlegest \(\displaystyle RT \)-vel.
Csakhogy ebben a szerkesztésben a \(\displaystyle T \) pontra két lehetőséget kapunk a szerint, hogy az elforgatott szakasz melyik végpontja kerül \(\displaystyle P \)-be. A két lehetőség két ellentétes körüljárású négyzetet ad.
Speciális esetek. Ha \(\displaystyle R = T \), de \(\displaystyle P \ne T \), akkor van végtelen sok különböző négyzet, mégpedig bármilyen irányú oldalegyeneshez egy, kivéve a \(\displaystyle PR \)-rel párhuzamos vagy merőleges irányt. Ha \(\displaystyle PTR \) kollineáris, de \(\displaystyle R \ne T \), akkor nincs megoldás.
Ha a feladatkiírást úgy értelmezed, hogy \(\displaystyle P \) az \(\displaystyle AB \) szakaszon legyen stb, akkor minden megoldást ellenőrizni kell, hogy az adott pontok tényleg a szakaszokon vannak, nem az oldalegyenesek valamely másik részén. Ekkor a tipikus esetben legfeljebb egy megoldás lehet.
|
| Előzmény: [1905] w, 2016-10-13 18:46:54 |
|
| [1905] w | 2016-10-13 18:46:54 |
 Adottak a síkon a \(\displaystyle P,Q,R,S\) pontok. Szerkesszünk olyan \(\displaystyle ABCD\) négyzetet, melyre \(\displaystyle P\in AB\), \(\displaystyle Q\in BC\), \(\displaystyle R\in CD\), \(\displaystyle S\in DA\)!
|
|
| [1904] Sinobi | 2016-07-27 00:31:12 |
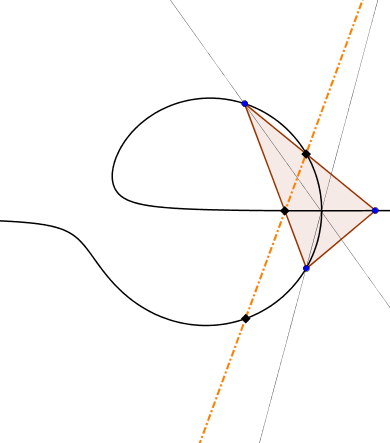
 189. feladat: Legyen &tex;\displaystyle \vartheta&xet; két, közös végpontú szakasz, HI és IJ ekvioptikus görbéje (azaz: azon P pontok mértani helye, melyekre HPJ egyik szögfelezője átmegy I-n)
Bizonyítsuk be, hogy ha A,B,C &tex;\displaystyle \in \vartheta&xet; háromszög a görbén fekszik úgy, hogy ABC beírt körének középpontja I, akkor EFG egy egyenesre illeszkednek, amennyiben &tex;\displaystyle \{E,F,G\} = ABC \cap \vartheta&xet; A,B,C-tól különböző metszéspontjai.
|
 |
|
| [1903] Sinobi | 2016-05-30 13:42:45 |
 > Adott a síkon négy egyenes. Tekintsük az összes kúpszeletet, amelyek érintik ezt a négy egyenest. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
Ezt is én, nem lett megoldva (számozni kéne??). A válasz az hogy a Newton érintőnégyszög tétele értelmében az átlók felezőpontjait összekötő egyenesen lesz. (Ellipszisre úgy megy, hogy körré affinítod, és alkalmazod Newton tételét. Hiperbolára mondjuk úgy, hogy veszed ugyanazt a bizonyítást a Minkowski síkon, és megkapod derékszögű hiperbolára a tételt. Másik lehetőség, hogy tükrözöl a kúpszelet középpontjára, és akkor a Brianchon azonnal adja.) (.. minden testre működik ez a bizonyítás, nem? Létezik 4 egyeneshez mindig érintő kúpszelet, kúpszeletnek középpont, középpontnak tükrözés, illetve Brianchon..?)
.. mi a helyzet magasabb dimenzióban? Két adott másodrendű felület lineáris kombinációnak a középpontjainak mi a mértani helye? N síkot érintő másodrendű felületek középpontjainak?
(Én nem tudom.)
.. van valakinek szakirodalma másodrendű felületsorokról?
|
| Előzmény: [1776] Sinobi, 2013-12-11 18:15:18 |
|
| [1902] Sinobi | 2016-05-26 03:49:47 |
 >> Kúpszeletsor középpontjának mértani helye?
> Sejtés: a négy megadott pont (A,B,C,D) által meghatározott összes szakasz felezőpontjára illeszthető kúpszelet.
Egy geometriai megoldás:
Ha a négy pont konkáv, akkor egy ortogonális négyesbe affinítod őket. Ekkor az összes rajtuk átmenő kúpszelet merőleges parabola lesz, és a középpontjuk a négyszög Feuerbach-körén lesz. Ezt nem nehéz belátni.
Ha a négy pontod konvex, akkor húrnégyszöggé affinítod, és, még sokkal egyszerűbben be lehet látni hogy az ilyen középpontok mértani helye egy merőleges hipike. (Nagyon érdemes észben tartani, hogy merőleges hipikét kapsz akkor ha egy sugársort csúsztatva tükrözöl és elmetszel önmagával, és általában csak ilyenkor.)
(Ha a négy pont trapéz akkor közelíted nem trapézokkal, a mértani hely is folytonosan fog változni.)
Ez egy nagyon erős és jól használható módszer, érdemes észbentartani. (Nem is gondolná az ember, hogy mi minden affin/vektoros, ami elsőre nem tűnik annak.)
|
| Előzmény: [1750] w, 2013-10-30 22:24:46 |
|
|
| [1900] sakkmath | 2016-03-14 20:46:35 |
 A 188. feladat a 185. köpönyegéből bújt elő, ezért HoA [1899]-es szép megoldása - átbetűzések után - megoldja 188-at is.
Utóbbira felteszek egy új megoldást, amely a Casey-tételkört érinti oda-vissza. Egyúttal köszönöm W-nek, hogy a témáról alapos összegzést adott [1894]-[1895]-ben.
|
 |
|
| [1899] HoA | 2016-02-15 11:00:17 |
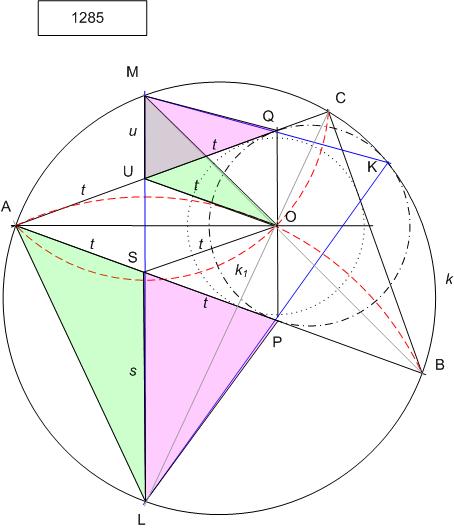
 Ha már ismét előjött Sawayama, felteszem elemi megoldásomat a 185. feladatra ( KöMaL 1285. feladat, ld itt [1879]) mielőtt feledésbe merül.
Legyen a körülírt kör &tex;\displaystyle k&xet;, az AB-t P-ben , AC-t Q-ban érintő kör &tex;\displaystyle k_1&xet; , külső hasonlósági pontjuk K, erről fogjuk megmutatni, hogy rajta van &tex;\displaystyle k&xet;-n. Itt is igaz, mint [1880] –ban, hogy a hasonlóságban P ill Q megfelelői az AB, AC ívek L ill. M felezőpontjai. Ismert, hogy az M középpontú MA sugarú és az L középpontú LA sugarú körök O-n is átmennek, ezért AO e két kör közös húrja, centrálisuk, LM ennek felező merőlegese. A BO és CO szögfelezők &tex;\displaystyle k&xet;-t M-ben ill. L-ben metszik. LM metszéspontja AB-vel ill. AC-vel legyen S ill. U. AO szögfelező, így ASOU rombusz, oldalhossza legyen t. A párhuzamos szelők tétele miatt t hosszúságú SP és UQ is. LSA és OUM &tex;\displaystyle \Delta&xet; -ek hasonlók, mert S-nél ill. U-nál lévő szögeik váltószögek, A-nál ill. M-nél lévő szögeik pedig az LB ívhez tartozó kerületi szögek. Innen az oldalak arányára
&tex;\displaystyle t / s = u/t &xet;
Emiatt hasonlóak a &tex;\displaystyle h_1&xet; = PSL és &tex;\displaystyle h_2&xet; = MUQ &tex;\displaystyle \Delta&xet;-ek, mert megegyeznek két oldal arányában és a közbezárt szögben ( S –nél ill. U-nál fekvő szögük az ASOU rombusz ASU = AUS félszögének csúcsszögei ) . &tex;\displaystyle h_1&xet;-hez és &tex;\displaystyle h_2&xet;-höz hasonló a &tex;\displaystyle h_3&xet; = KML &tex;\displaystyle \Delta&xet; , mert két szöge ( M-nél ill. L-nél ) megegyezik az előbbiek egy-egy, egymásnak nem megfelelő szögével. LKM &tex;\displaystyle \angle&xet; = MUQ &tex;\displaystyle \angle&xet;= AUS &tex;\displaystyle \angle&xet; = 90 – &tex;\displaystyle \alpha&xet;/2 , ami megegyezik az ML = MA + AL ívhez tartozó &tex;\displaystyle \beta&xet;/2 + &tex;\displaystyle \gamma&xet;/2 kerületi szöggel, K tehát rajta van k-n.
|
 |
| Előzmény: [1893] Sinobi, 2016-01-23 21:43:39 |
|
| [1898] Sinobi | 2016-01-31 20:53:15 |
 amúgy ez a koaxális körös, ez koaxiális akar lenni, vagy, valahonnan máshonnan kapta a nevét? Úgy sem látom több értelmét, de legalább valamit jelent. (valami olyat, amit én is ismerek)
|
| Előzmény: [1894] w, 2016-01-24 00:14:41 |
|
| [1897] Sinobi | 2016-01-31 19:19:19 |
 Hát, a Ptoleimaiosz-ból (és a koaxális körök lemmájából) azonnal adódik:
Ha az alsó érintési pont D, D-ből a megfelelő távolságok &tex;\displaystyle a,b,c&xet; (ahol &tex;\displaystyle a=b&xet;); és l az az arány, hogy l*i az i. pont &tex;\displaystyle k_1&xet;-hez húzott érintőjének a hossza, akkor:
&tex;\displaystyle \frac{AB+BC}{AC}=\frac{l(a+b)+BC}{l(a+c)}&xet;
ahol a Ptolemaiosz-tétel értelmében
&tex;\displaystyle BC \cdot a = c \cdot l (a+b) ~ + ~ b \cdot l (a+c)=3 l a c + l a^2&xet;
azaz &tex;\displaystyle BC=3 l c + l a&xet;, és &tex;\displaystyle \frac{AB+BC}{AC}=3&xet;.
(Valószínűleg kis módosítással adódik, hogy ha U nem az AB felezőpontja, és, D nem az AB felező merőlegesén van (hanem az egyik Apollóniusz-körén), akkor, ez az arány így is konstans. Bár az előbb 'véletlen' volt, hogy kiestek a dolgok.)
.. valaki ismer erre szépet? Nézegettem az előbb belinkelt Poncelet-eset, ott hasonló konfigurációk vannak, de, ahogy néztem pont ez nincs. .. mert az összefüggés nagyon szép rövid, egyszerű.
|
| Előzmény: [1896] spongya, 2016-01-31 16:43:50 |
|
| [1896] spongya | 2016-01-31 16:43:50 |
 Ez rövid volt, gratula!
Geom.progival nézegetve, az oldalak hosszaira ez állhat:
&tex;\displaystyle {AB + BC = {\it 3}\cdot AC}.&xet;
Bizonyítsuk be a fenti összefüggést! (188/b. feladat)
|
| Előzmény: [1893] Sinobi, 2016-01-23 21:43:39 |
|
| [1895] w | 2016-01-24 00:16:12 |
 Casey-tétel. Adott a &tex;\displaystyle k&xet; irányított kör és az azt &tex;\displaystyle A,B,C,D&xet; pontokban érintő &tex;\displaystyle \alpha,\beta,\gamma,\delta&xet; irányított körök. Ekkor ha &tex;\displaystyle ABCD&xet; négyszög konvex, akkor
| &tex;\displaystyle t_{\alpha\beta}t_{\gamma\delta}+ t_{\alpha\delta}t_{\beta\gamma}=t_{\alpha\gamma}t_{\beta\delta}.&xet; | (*) |
Casey-tétel megfordítása. Adott négy irányított kör a síkon: &tex;\displaystyle \alpha,\beta,\gamma,\delta&xet;. Ekkor ha teljesítik a &tex;\displaystyle (*)&xet; összefüggést, akkor van olyan irányított &tex;\displaystyle k&xet; kör vagy olyan egyenes, amely mind a négyet érinti.
&tex;\displaystyle &xet;
Bizonyítás. Maga a Casey-tétel egyszerű következménye a &tex;\displaystyle (2)&xet; képletnek. Ebből a képletből behelyettesítéssel látható, hogy &tex;\displaystyle (*)&xet; fennállása nem függ a négy kör sugarától, csupán a négy érintési pont helyzetétől. Vagyis vehetjük a köröket ponttá fajulónak, és ezzel a Ptolemaiosz-tételre vezettük vissza a Casey-t.
Igazából Sharygin szerint lehetünk ügyesebbek is: egy mozdulattal mind a Casey-tételt, mint speciális esetét, a Ptolemaiosz-tételt is levezethetjük, ha a négy körsugarat inkább úgy vesszük fel, hogy &tex;\displaystyle \alpha&xet; és &tex;\displaystyle \delta&xet; ponttá fajuljon és &tex;\displaystyle \beta,\gamma&xet; az &tex;\displaystyle AD&xet; húrt érintse. Ekkor a &tex;\displaystyle (*)&xet;-beli mennyiségek mind az &tex;\displaystyle AD&xet; szakaszon jelennek meg, és ezekre &tex;\displaystyle (*)&xet;-ot már gyerekjáték ellenőrizni.
A Casey-tétel akkor is igaz marad, ha &tex;\displaystyle k&xet; nem kör, hanem egyenes. Sőt, éppen ugyanaz a triviális állítás, mint az, amit az imént &tex;\displaystyle AD&xet; húron megjelenítettünk.
A megfordítás pedig klasszikus tételmegfordítás: magát a tételt használó indoklása van.
Mindenekelőtt jegyezzük meg, hogy &tex;\displaystyle (1)&xet; szerint ha mind a négy irányított körünk sugarát ugyanazzal a mennyiséggel változtatjuk, azzal minden közös érintőszakasz ugyanakkora marad, és közben jól láthatóan a négy kört érintő irányított kör (vagy egyenes) léte sem csorbul. Emiatt változathatjuk a körsugarakat úgy, hogy mondjuk &tex;\displaystyle \alpha&xet; egyetlen &tex;\displaystyle A&xet; ponttá fajuljon.
Hogyha a &tex;\displaystyle \beta,\gamma,\delta&xet; körök ekkor szintén pontok lesznek, akkor a Ptolemaiosz-tétel megfordítása miatt készen vagyunk. Egyéb esetben pedig az apollóniuszi probléma miatt van két különböző irányított kör (vagy egyenes), ami &tex;\displaystyle \beta,\gamma,\delta&xet; mindegyikét érinti: legyenek ezek &tex;\displaystyle k_1&xet; és &tex;\displaystyle k_2&xet;.
Vezessük be még a &tex;\displaystyle \lambda=\frac{t_{A\beta}}{t_{A\delta}}&xet; és &tex;\displaystyle \mu=\frac{t_{A\gamma}}{t_{A\delta}}&xet; jelölést. Ekkor a feltétel szerint
&tex;\displaystyle \mu=\frac{t_{A\gamma}}{t_{A\delta}}=\frac{t_{A\beta}t_{\gamma\delta}+t_{A\delta}t_{\beta\gamma}}{t_{A\delta}t_{\beta\delta}}=\frac{\lambda t_{\gamma\delta}+t_{\beta\gamma}}{t_{\beta\delta}}.&xet;
A Hraskó-féle koaxális körös lemma szerint &tex;\displaystyle A&xet; rajta van azon az &tex;\displaystyle \ell&xet; körön/egyenesen, amit a &tex;\displaystyle \lambda&xet; arány és &tex;\displaystyle \beta,\delta&xet; kör meghatároz, illetve azon az &tex;\displaystyle m&xet; körön/egyenesen, amit &tex;\displaystyle \mu&xet; arány és &tex;\displaystyle \gamma,\delta&xet; kör meghatároz.
Tegyük össze a két előbbi definíciót! Az &tex;\displaystyle \ell&xet; és &tex;\displaystyle k_1&xet; két pontban metsz, hisz &tex;\displaystyle k_1&xet; érinti &tex;\displaystyle \beta&xet;-t és &tex;\displaystyle \delta&xet;-t. Az is igaz, hogy éppen az egyik metszéspont a &tex;\displaystyle k_1&xet; kör azon ívére esik, ami nem tartalmazza a &tex;\displaystyle k_1&xet;-nek &tex;\displaystyle \gamma&xet;-val való érintési pontját. Legyen ő &tex;\displaystyle A_1&xet;. Ez azért használ, mert a Casey-tételt felírhatjuk:
&tex;\displaystyle t_{A_1\gamma}t_{\beta\delta}=t_{A_1\beta}t_{\gamma\delta}+t_{A_1\delta}t_{\beta\gamma},&xet;
&tex;\displaystyle \frac{t_{A_1\gamma}}{t_{A_1\delta}}=\frac{\lambda t_{\gamma\delta}+t_{\beta\gamma}}{t_{\beta\delta}}=\mu,&xet;
vagyis &tex;\displaystyle A_1\in m&xet;. Hasonlóan felvéve &tex;\displaystyle k_2&xet;-n az &tex;\displaystyle A_2&xet; pontot, elmondható, hogy &tex;\displaystyle A_2\in \ell&xet;-ből &tex;\displaystyle A_2\in m&xet; következik.
Tehát &tex;\displaystyle A,A_1,A_2&xet; három pont, ami &tex;\displaystyle \ell\cap m&xet; metszetbe tartozik. Két kör/egyenes legfeljebb két pontban metszhet, ezért vagy &tex;\displaystyle A&xet; egybeesik &tex;\displaystyle A_1,A_2&xet; egyikével és készen vagyunk, vagy pedig marad a kellemetlen &tex;\displaystyle A_1=A_2&xet; eset.
Azt az esetet, hogy &tex;\displaystyle A_1=A_2&xet;, azzal gyógyíthatjuk, hogy észrevesszük, hogy ilyenkor &tex;\displaystyle \ell&xet; és &tex;\displaystyle m&xet; érintkeznek, és úgy &tex;\displaystyle A=A_1=A_2&xet; következik. Azért lesz &tex;\displaystyle \ell&xet; és &tex;\displaystyle m&xet; érintő, mert ha &tex;\displaystyle \lambda&xet;-t lecseréljük valami &tex;\displaystyle \lambda’\to \lambda&xet;-ra, úgy a kapott &tex;\displaystyle A_1’&xet; és &tex;\displaystyle A_2’&xet; pontok már különbözőek, és ez a két különböző metszéspontja a nyert &tex;\displaystyle \ell’&xet; és &tex;\displaystyle m’&xet; görbéknek; mivel &tex;\displaystyle A_1’&xet; és &tex;\displaystyle A_2’&xet; is az &tex;\displaystyle A_1=A_2&xet;-höz fog tartani, ezért &tex;\displaystyle \ell&xet; és &tex;\displaystyle m&xet; „mindkét metszéspontja” &tex;\displaystyle A_1=A_2&xet;, vagyis érintkeznek. (Ez ilyenformán meggyőző érvelésnek hangzik, de precizzé tehető.)
A bizonyítás ezzel pedig véget ért.
|
|
| [1894] w | 2016-01-24 00:14:41 |
 Leírom saját tolmácsolásomban a Casey-tételt és megfordítását, bizonyítással együtt.
Az "oda irány" az angol Wikipédián látott bizonyítás diszkusszióval való helyessé tételével adódott. A megfordítás bizonyítása a Sharygin: Problems in Plane Geometry c. könyvben található meg.
Sajnálom, ábrá(ka)t nem csatolok, az Olvasónak papírt és rajzszerszámot kell majd ragadnia, ha nem kívánja fejben elképzelni az ábrákat.
Szükségünk lesz az irányított kör fogalmára. Egy irányított kör egy kör a síkon, amihez egy &tex;\displaystyle \epsilon\in\{1,-1\}&xet; előjelet rendelünk. Azt mondjuk, hogy az irányított kör sugara &tex;\displaystyle R=\epsilon |R|&xet;, ahol &tex;\displaystyle |R|&xet; a szokásos értelemben vett sugár. Azt mondjuk, hogy &tex;\displaystyle x,y&xet; irányított körök érintik egymást, hogyha irányítatlan köreik belülről érintik egymást és &tex;\displaystyle x,y&xet; azonos irányítású, vagy pedig kívülről érintik egymást és &tex;\displaystyle x,y&xet; ellentétes irányítású. (Például: egybeeső körök belülről érintik egymást, ezért azonos irányításnál érintőek, különböző irányításnál nem. Egy ponttá fajuló kör irányítása mindegy, mert &tex;\displaystyle 0&xet; a sugara.)
Jelölje még &tex;\displaystyle x,y&xet; irányított körökhöz &tex;\displaystyle t_{xy}&xet; az &tex;\displaystyle x&xet; és &tex;\displaystyle y&xet; körök közös „külső” érintőszakaszának a hosszát. Vagyis ha &tex;\displaystyle x,y&xet; azonos irányítású, a külső érintőszakaszt, ha különböző irányítású, a belső érintőszakaszt kell venni.
Legyen &tex;\displaystyle x,y&xet; irányított körök középpontja &tex;\displaystyle O_x,O_y&xet;, sugara &tex;\displaystyle R_x,R_y&xet;. Ekkor Pitagorasz-tétel szerint
| &tex;\displaystyle t_{xy}=\sqrt{O_xO_y^2+(R_x-R_y)^2},&xet; | (1) |
és ebből levezethető, hogy ha &tex;\displaystyle x,y&xet; rendre az &tex;\displaystyle X,Y&xet; pontban érint egy &tex;\displaystyle R_k&xet; sugarú irányított &tex;\displaystyle k&xet; kört, akkor
| &tex;\displaystyle t_{xy}=\sqrt{\left(1-\frac{R_x}{R_k}\right)\left(1-\frac{R_y}{R_k}\right)} \cdot |XY|.&xet; | (2) |
Fontos még az apollóniuszi problémáról szót ejteni. Tulajdonképpen következik belőle, hogy ha adott három irányított kör, &tex;\displaystyle x,y,z&xet;, melyek valamelyikének nem nulla a sugara, akkor két olyan irányított kör is adható, melyek &tex;\displaystyle x,y,z&xet; mindegyikét érintik.
Még egy lemmát használunk, amit koaxális körök lemmájaként is hallottam, bár én elsőként ebben a cikkben láttam, nevezetesen hogy ha adott két kör, akkor az olyan pontok halmaza, melyekre a két körhöz húzott érintők hosszainak aránya &tex;\displaystyle \lambda&xet;, kör, ha &tex;\displaystyle \lambda\neq 1&xet;, és épp a hatványvonal, ha &tex;\displaystyle \lambda=1&xet;. (Amúgy ha a két körünk ponttá fajul, épp a pontok Apollóniusz-köreit kapjuk.)
Ennyi bevezetés után rátérek a két állítás kimondására.
|
|
| [1893] Sinobi | 2016-01-23 21:43:39 |
 Sawayama => egy &tex;\displaystyle ABC&xet; háromszög két oldalát érintő kör pontosan akkor érinti a &tex;\displaystyle k&xet; körülírt körét is, ha az érintési pontok tükrösek a beírt kör &tex;\displaystyle I&xet; középpontjára.
Ez alapján: t tükörképe I-re átmegy U-n, tehát átmegy Z-n is, ezt akartuk belátni.
|
 |
| Előzmény: [1890] sakkmath, 2015-12-21 02:01:39 |
|
| [1892] w | 2016-01-23 11:18:59 |
 Megpróbálom hamarosan leírni a preciz kimondását a tételnek és a megfordításnak. Van bizonyítás is hozzájuk. (Szeretném viszont az irányításokat is rendbetenni.)
|
| Előzmény: [1891] HoA, 2016-01-22 16:42:16 |
|
| [1891] HoA | 2016-01-22 16:42:16 |
 Mit értesz megfordításon? Ahogy én ismerem, ez a tétel adott módon érintkező 1 + 4 kör közös érintőszakaszai közötti méretes összefüggést állít. Mi ennek a megfordítottja?
|
| Előzmény: [1889] sakkmath, 2015-12-13 13:13:22 |
|
| [1890] sakkmath | 2015-12-21 02:01:39 |
 188. feladat: Adott egy &tex;\displaystyle k&xet; kör az &tex;\displaystyle AB&xet; húrral, s annak &tex;\displaystyle U&xet; felezéspontjával. Legyen adott a &tex;\displaystyle k_1&xet; kör úgy, hogy érintse az &tex;\displaystyle AB&xet; szakaszt &tex;\displaystyle U&xet;-ban és érintse a &tex;\displaystyle k&xet; kört. A &tex;\displaystyle k_1&xet; kör &tex;\displaystyle A&xet;-n átmenő, &tex;\displaystyle AB&xet;-től különböző érintőjét jelöljük &tex;\displaystyle t&xet;-vel. A &tex;\displaystyle k&xet; kör és &tex;\displaystyle t&xet; &tex;\displaystyle A&xet;-tól különböző metszéspontja &tex;\displaystyle C&xet;, a &tex;\displaystyle BC&xet; szakasz felezéspontja &tex;\displaystyle Z&xet;. Tekintsük azt a &tex;\displaystyle k_2&xet; kört, amelyik a &tex;\displaystyle BC&xet; egyenest &tex;\displaystyle Z&xet;-ben érinti és érinti az &tex;\displaystyle AC&xet; egyenest. Bizonyítsuk be, hogy &tex;\displaystyle k_2&xet; és &tex;\displaystyle k&xet; érinti egymást.
|
|
| [1889] sakkmath | 2015-12-13 13:13:22 |
 Létezik-e a Casey-tétel megfordításának elemi geometriai bizonyítása?
|
|
| [1888] Sinobi | 2015-10-29 11:11:13 |
 Aha. És az igaz-e, hogy a köréírt körük középpontja is egyenletesen, egyenesen mozog? (például limeszben mozoghat egyenesen, hogy egyébként hiperbola/harmadrendű a mértani helye)
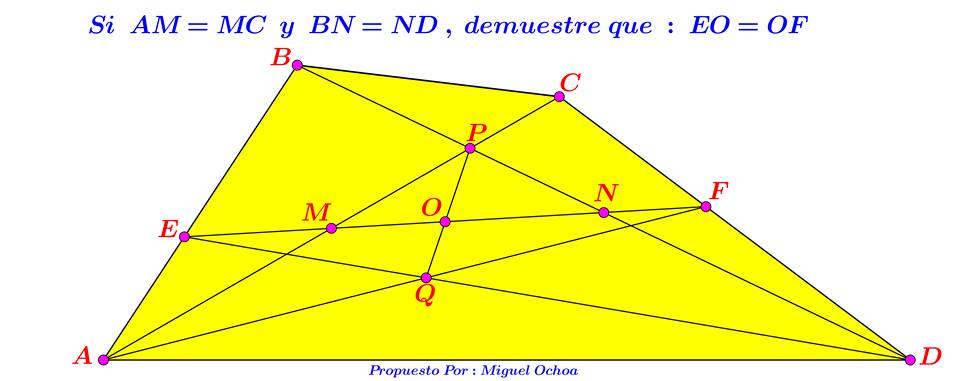
Ha nem ajánlasz mást, akkor a 187. feladat legyen egy szokásos, szimpla egyeneses-távolságos (csak mert az én megoldásom ronda, és nem találok szépet):
&tex;\displaystyle ABCD&xet; négyszögben &tex;\displaystyle M&xet;,&tex;\displaystyle N&xet; &tex;\displaystyle :=&xet; mid(&tex;\displaystyle AC&xet;), mid(&tex;\displaystyle BD&xet;); &tex;\displaystyle E&xet;,&tex;\displaystyle F&xet; &tex;\displaystyle :=&xet; &tex;\displaystyle MN \cap AB&xet;, &tex;\displaystyle MN \cap CD&xet;; &tex;\displaystyle P&xet; &tex;\displaystyle :=&xet; &tex;\displaystyle AC \cap BD&xet;; &tex;\displaystyle Q&xet; &tex;\displaystyle :=&xet; &tex;\displaystyle ED \cap AF&xet;, (lásd ábra), bizonyítsd be, hogy &tex;\displaystyle QP&xet; felezi az &tex;\displaystyle EF&xet; szakaszt.
Aztán, valaki ajánljon mást (mondjuk, aki megoldja).
|
 |
| Előzmény: [1887] Fálesz Mihály, 2015-10-26 15:34:28 |
|
| [1887] Fálesz Mihály | 2015-10-26 15:34:28 |
 Ebben a formában nem igaz. Például, ha a négy pont &tex;\displaystyle A(t)=(-t,0)&xet;, &tex;\displaystyle B(t)=(t,0)&xet;, &tex;\displaystyle C(t)=(2t,1)&xet; és &tex;\displaystyle D(t)=(-2t,1)&xet;, akkor &tex;\displaystyle t=0&xet; esetén két-két pont egybeesik, &tex;\displaystyle t\ne0&xet; esetén pedig a négy pont egy szimmetrikus trapéz csúcsai. A négy pont tehát mindig egy körön van. Ugyanakkor a négy sebességvektor &tex;\displaystyle (-1,0)&xet;, &tex;\displaystyle (1,0)&xet;, &tex;\displaystyle (2,0)&xet; és &tex;\displaystyle (-2,0)&xet; egy egyenesre esik.
Az viszont igaz, hogy a négy sebességvektor egy körre vagy egy egyenesre esik. Ha valamelyik két sebességvektor egyenlő, akkor a sebességvektorok triviálisan egy körön vagy egyenesen vannak. Tegyük tehát fel, hogy a négy sebességvektor különböző. Tekintsük a pontokat komplex számoknak, és vizsgáljuk a
&tex;\displaystyle
\big(A(t),B(t),C(t),D(t)\big) =
\frac{C(t)-A(t)}{B(t)-C(t)}:\frac{D(t)-A(t)}{B(t)-D(t)}
&xet;
kettősviszony határértékét, ha &tex;\displaystyle t\to\infty&xet;. A négy pont akkor és csak akkor van egy körön vagy egy egyenesen, ha a kettősviszony nem értelmes, mert valamelyik két pont egybeesik (ilyen legfeljebb 4 pillanatban történhet), vagy a kettősviszony tisztán valós. A ketősviszony tehát véges sok ponttól eltekintve valós, így a határértéke is tisztán valós. A határértéke viszont éppen a sebességvektorokból készített kettősviszony:
&tex;\displaystyle
\lim_{t\to\infty} \big(A(t),B(t),C(t),D(t)\big) =
\lim_{t\to\infty}\frac{\frac{C(t)}t-\frac{A(t)}t}{\frac{B(t)}t-\frac{C(t)}t}:\frac{\frac{D(t)}t-\frac{A(t)}t}{\frac{B(t)}t-\frac{D(t)}t} =
\frac{C'-A'}{B'-C'}:\frac{D'-A'}{B'-D'} =
(A',B',C',D'),
&xet;
így ez is valós, tehát a négy sebességvektor, &tex;\displaystyle A'&xet;, &tex;\displaystyle B'&xet;, &tex;\displaystyle C'&xet; és &tex;\displaystyle D'&xet; egy körön vagy egy egyenesen van.
|
| Előzmény: [1886] Sinobi, 2015-10-24 10:24:25 |
|
| [1886] Sinobi | 2015-10-24 10:24:25 |
 186. feladat: Igaz-e, hogy ha 4 pont egyenletes sebességgel mozog a síkon úgy, hogy minden t időpillanatban egy körre esnek, akkor a sebességvektoraik végpontjai is egy körre esnek?
|
|
|
| [1884] Hajba Károly | 2015-08-14 08:22:52 |
 Köszi. Közben a kép alapján ráleltem a MathPuzzle az első linkeddel teljesen hasonló oldalára.
Hiányoltam az ún. Cairo csempézést, de ez alapján rájöttem, hogy az a 2-es és 4-es típusba is beletartozik, ahogy sejtettem is az átfedás lehetőségét.
Mások rácspontokon keresztül osztályoznak, de a többlet rácspontnál a szögnek 180 fokosnak kell lennie.
|
| Előzmény: [1883] Róbert Gida, 2015-08-13 17:57:01 |
|
|
| [1882] Hajba Károly | 2015-08-12 16:15:52 |
 Most olvastam egy cikket a sík ötszögekkel történő lefedéséről, amely cikk erre az angol cikkre hivatkozik.
Angolul nem értek annyira, hogy megértsem a forráscikket, a magyar cikkben meg szerintem nincs minden feltétel leírva.
Lényeg és ami engem érdekelne, hogy mi külön-külön a 15 féle lefedési forma egyedisége?

Úgy érzem, hogy némely lefedések valamely feltételben hasonlóak, így csoportosíthatók és a csoporton belül egyéb, külön feltételek megléte miatt különbözik a csoport többi tagjától. És azt sem tartom kizártnak, hogy egyes csoportok átfedőek.
Minden infó érdekel és előre köszönök minden segítséget.
|
|
| [1881] HoA | 2015-03-16 14:23:18 |
 A megoldás szép és egyszerű, de én a Pascal-tételt, mint a projektív geometria tárgyába tartozót, nem érzem elég eleminek. :-)
|
| Előzmény: [1880] w, 2015-03-11 17:51:23 |
|
| [1880] w | 2015-03-11 17:51:23 |
 Tekintsük inkább azt az &tex;\displaystyle \omega&xet; kört, amely a körülírt &tex;\displaystyle k&xet; kört belülről érinti &tex;\displaystyle K&xet;-ban, és érinti még az &tex;\displaystyle AB,AC&xet; félegyeneseket &tex;\displaystyle X&xet; és &tex;\displaystyle Y&xet; pontban.
Az érintés miatt &tex;\displaystyle \omega&xet; kör &tex;\displaystyle k&xet;-ba vihető egy nagyítással &tex;\displaystyle K&xet;-ból, és e nagyítással &tex;\displaystyle X&xet; képe olyan &tex;\displaystyle L&xet; pont &tex;\displaystyle k&xet;-nak a &tex;\displaystyle C&xet;-t nem tartalmazó &tex;\displaystyle AB&xet; ívén, amelyben húzott érintő párhuzamos &tex;\displaystyle AB&xet;-vel: ez éppen az &tex;\displaystyle AB&xet; ív felezőpontja. Hasonlóan, &tex;\displaystyle Y'&xet; pedig a megfelelő &tex;\displaystyle AC&xet; ív &tex;\displaystyle M&xet; felezőpontja lesz.
Ha most alkalmazzuk a Pascal-tételt a &tex;\displaystyle KLCABM&xet; húrhatszögre, adódik, hogy &tex;\displaystyle KL\cap AB=X&xet;, &tex;\displaystyle LC\cap BM=O&xet; (ez a beírt kör középpontja, hisz két szögfelező metszéspontja) és &tex;\displaystyle CA\cap MK=Y&xet; egy egyenesre esik. Továbbá mivel &tex;\displaystyle AB,AC&xet;-t érinti, így &tex;\displaystyle \omega&xet; szimmetrikus &tex;\displaystyle BAC\angle&xet; szögfelezőjére, így &tex;\displaystyle AO&xet; és &tex;\displaystyle XY&xet; merőleges lesz. Tehát &tex;\displaystyle X=P&xet;, &tex;\displaystyle Y=Q&xet; és készen vagyunk.
(Egyébként ez a feladat is a Sawayama-lemma következménye.)
|
 |
| Előzmény: [1879] HoA, 2015-03-11 15:21:55 |
|
| [1879] HoA | 2015-03-11 15:21:55 |
 Már régen nem szerepelt itt a téma saját számozású feladata. Ha nem tévedek, az [1742] -beli "N+1-edik" feladatot nem számítva 184. volt az utolsó. Legyen tehát a
185. feladat : Az &tex;\displaystyle ABC&xet; háromszögbe írt kör &tex;\displaystyle O&xet; középpontján át az &tex;\displaystyle AO&xet; szögfelezőre állított merőleges az &tex;\displaystyle AB&xet; olalt &tex;\displaystyle P&xet;-ben, &tex;\displaystyle AC&xet;-t &tex;\displaystyle Q&xet;-ban metszi. Rajzoljuk meg azt a kört, amely &tex;\displaystyle AB&xet;-t &tex;\displaystyle P&xet;-ben , &tex;\displaystyle AC&xet;-t &tex;\displaystyle Q&xet;-ban érinti. Bizonyítsuk be, hogy ez a kör érinti a háromszög körülírt körét.
Ez valójában egy "Lejárt határidejű KöMaL feladat" ( 1285. ) , de annyira lejárt, hogy inkább ide teszem. Annak ikdején a Lapban egy számításos megoldás jelent meg. Itt a fórumon a GEOMETRIA témában már találkoztunk ezzel a körrel ( ld. 151. feladat [1217] ) . Az ott következő hozzászólásokban közel kerültünk a mostani feladat inverziós megoldásához. Ezért most egy elemi geometriai megoldás reményében teszem fel.
|
|
| [1878] csábos | 2014-10-03 09:09:14 |
 Kiindultam a HoA féle szinuszos egyenletből. Felvettük ,,véletlenszerűen" az együtthatók értékeit, és ekkor &tex;\displaystyle \cos\alpha&xet;-ra egy negyedfokú egyenletet kaptunk. Az a kérdés, hogy ennek az egyenletnek a gyökei szekeszthetőek-e. Az egy igazi jó kizáró ok lenne, ha ez egy harmadfokú, &tex;\displaystyle Q&xet; fölött felbonthatalan polinom lenne. Sajnos nem az. Ha valaki találna paramétereket úgy, hogy ez egy első és harmadfokú szorzata lenne, és az elsőfokú gyöke nem megoldás, akkor nyilvánvalóbb lenne az indoklás. Ezért kis érdeklődés és lapozgatás után rábukkantam arra az összefüggésre, hogy ha találunk egy olyan prímet, ami fölött ennek a polinomnak van fölbonthatatlan, páratlanfokú osztója, akkor nem szerkeszthető a gyöke. Kézenfekvő volt az 5.
|
| Előzmény: [1876] Bátki Zsolt, 2014-10-02 20:43:53 |
|
|
| [1876] Bátki Zsolt | 2014-10-02 20:43:53 |
 Nem mindent fogtam fel. Bennem lehet a hiba. A köbgyök 3 meggyőzőnek tűnik, mivel ezt javasoltam is. Itt egy új gondolatmenet. (Nem tudom, hogy kell rajzot küldeni) Vegyünk egy egység kört az origóban. Vegyünk fel egy D pontot rajta, ami a keresendő minimális távolságú A-tól és B-től. Vegyük fel az A-t az x tengelyen. Ekkor könnyen meghatározható az a félegyenes (f) D-ből indul és amin a B-nek kell lennie. Legyen 'e' egyenes ami az x koordinátával bezárt szöge háromszorosa a AOD szögnek, és az origóból indul. Nyilván az 'e' és 'f' metszéspontja jó megoldás a B pontra.
Tehát O,D,A ismeretében B szerkeszthető. (ebben a speciális esetben) De O,A,B esetén D nem szerkeszthető, mert ahhoz a AOB szöget harmadolni kellene tudni. Remélem világos volt és nem rontottam el semmit.
Tehát általános esetben nem szerkeszthető.
(az hogy általános szög nem harmadolható, az bizonyított, de nem egyszerű)
|
|
| [1875] csábos | 2014-10-01 22:54:59 |
 Mindig mondta a matektanárom, hogy a térszemléletem olyan, mint a döglött kacsáé.
Akkor számoljunk. &tex;\displaystyle \cos\phi=a&xet;, &tex;\displaystyle \sin\phi=\sqrt{1-a^2}&xet;, &tex;\displaystyle t=1&xet;, &tex;\displaystyle u=\frac{1}{2}&xet;, &tex;\displaystyle v=2&xet;,&tex;\displaystyle w=3&xet; helyettesítéssel a
&tex;\displaystyle t\cos2\phi+u\sin2\phi=v\cos\phi+w\sin\phi&xet;
egyenletből
&tex;\displaystyle (2a^2-1)+a\sqrt{1-a^2}=2a+3\sqrt{1-a^2}&xet;
lesz. Átrendezve
&tex;\displaystyle 2a^2-2a-1=(3-a)\sqrt{1-a^2}&xet;
és négyzetre emelve, majd rendezve
&tex;\displaystyle 5a^4-14a^3+8a^2-8 =0 &xet;
adódik. Modulo 5 véve
&tex;\displaystyle a^3+3a^2-3 &xet;
Ennek nincs gyöke modulo 5. Tehát a bővítés foka &tex;\displaystyle F_5&xet; fölött 3, így &tex;\displaystyle Q&xet; fölött a 3 többszöröse, tehát nem szerkeszthető.
|
| Előzmény: [1874] jonas, 2014-10-01 06:04:14 |
|
|
| [1873] csábos | 2014-09-30 20:55:52 |
 Nem értek valamit. Ha egyszer egyenlő szögeket keresünk, akkor miért nem invertáljuk az A pontot a körre (A1), majd a képet összekötjük a B-ponttal. Ahol metszi a kört (M-ben), ott a megfelelő szögek és tükörképeik is megegyeznek. Vagy megint elnéztem valamit?
|
| Előzmény: [1872] HoA, 2014-09-30 16:02:07 |
|
| [1872] HoA | 2014-09-30 16:02:07 |
 A nem-szerkeszthetőség irányában ( vázlat, ha valakit érdekel, részletezem )
Kínálja magát a komplex síkon tárgyalás. Válasszuk úgy a koordinátarendszert és a hosszegységet, hogy C legyen az origóban és D az egységsugarú körön. Ekkor d ( = CD ) egységvektor. Az egyenlő szögekből következik, hogy (( a -d ) / d) x (( b -d ) /d ) valós. Ebből d = &tex;\displaystyle e^{i\phi}&xet; -vel &tex;\displaystyle \phi&xet; -re
&tex;\displaystyle t \cdot cos 2\phi + u \cdot sin 2\phi = v \cdot cos \phi + w \cdot sin \phi &xet;
alakú egyenlet adódik, ahol az együtthatók az adatokból szerkeszthetőek. Már csak erről kéne megmutatni, hogy általában euklideszi módon nem szerkeszthető a megoldás.
( Ellenpélda: Két adott ponton átmenő, adott kört érintő kör középpontja : legyen itt is az adott egységsugarú kör középpontja, C az origóban, az érintési pont D, A és B a körön kívül. Ekkor d ( = CD ) egységvektor, a szerkesztendő kör középpontja O = kd ( k valós ) . Felírva az | A - O | = k - 1 ill. | B - O | = k - 1 egyenleteket , d = &tex;\displaystyle e^{i\phi}&xet; -vel &tex;\displaystyle \phi&xet; -re itt
&tex;\displaystyle v \cdot cos \phi + w \cdot sin \phi = z&xet;
alakú egyenlet adódik, ahol az együtthatók az adatokból szerkeszthetők, és mint ismert ekkor &tex;\displaystyle cos \phi&xet; -re másodfokú egyenletet kapunk szerkeszthető együtthatókkal. )
|
| Előzmény: [1868] Bátki Zsolt, 2014-09-23 18:19:23 |
|
|
| [1870] emm | 2014-09-25 02:58:38 |
 Hullafáradtan egy próbálkozás, 100%, hogy elszámolva, de valami ilyesmi: Legyen az ellipszis két fókuszpontja &tex;\displaystyle (c,0)&xet; és &tex;\displaystyle (-c,0)&xet;, a kör sugara egységnyi, középpontja &tex;\displaystyle (u,v)&xet;. Ekkor azt az &tex;\displaystyle a>c&xet;-t keressük (nagytengely), amire
&tex;\displaystyle
x^2(c^2-a^2)+y^2a^2=a^2(c^2-a^2)
&xet;
&tex;\displaystyle
(x-u)^2+(y-v)^2=1
&xet;
egyenletrendszernek 1 megoldása van. Vagyis:
&tex;\displaystyle
x^2(c^2-a^2)+y^2a^2=a^2(c^2-a^2)((x-u)^2+(y-v)^2)
&xet;
-nek egy megoldása van. Mivel ez a megoldás egyértelmű, ezért a diszkrimináns 0.
&tex;\displaystyle -4 a^2 (a - c) (a + c) (-a^2 u^2 + c^2 u^2 - a^2 v^2 + a^4 v^2 +
c^2 v^2 - a^2 c^2 v^2 + 2 a^2 v y - 2 a^4 v y - 2 c^2 v y + &xet;
&tex;\displaystyle + 2 a^2 c^2 v y + y^2 - 2 a^2 y^2 + a^4 y^2 + c^2 y^2 - a^2 c^2 y^2)=0
&xet;
Ez is egyértelmű &tex;\displaystyle y&xet;-ra, így a diszkrimináns ismét 0, így &tex;\displaystyle a&xet;-ra az egyenlet:
&tex;\displaystyle
64 (-1 + a) a^4 (1 + a) (a - c)^3 (a + c)^3 (-u^2 + a^2 u^2 -c^2 u^2 - v^2 + a^2 v^2)=0
&xet;
Aminek meg az értelmes megoldása
&tex;\displaystyle a=\frac{\sqrt{\left(c^2+1\right) u^2+v^2}}{\sqrt{u^2+v^2}}\qquad a=1&xet;
Ez meg szerkeszthető, ebből &tex;\displaystyle y=\frac{c^2 v^2-u^2-v^2}{c^2 v}&xet; megvanmá, megoldható, és megvan &tex;\displaystyle x=(u^2 + c^2 u^2 + v^2)/(c^2 u)&xet; is. Nem egy szépségdíjas számolás, ilyenkor jó a számítógép.
|
| Előzmény: [1868] Bátki Zsolt, 2014-09-23 18:19:23 |
|
| [1869] marcius8 | 2014-09-24 12:18:21 |
 Egy ötlet: Legyenek az "e" ellipszis fókuszpontjai F1(+c;0), F2(-c;0), legyen az ellipszis félnagytengelye "a", legyen az ellipszis félkistengelye "b", ekkor az ellipszis egyenlete ismert. Legyen a "k" kör középpontja K(u;v) és sugara "r", ekkor a "k" kör egyenlete is ismert. Ami ismert: az "F1", "F2", "u", "v", "r". Az "a" értékét úgy kell meghatározni, hogy az ellipszis egyenletéből és a kör egyenletéből álló egyenletrendszernek pontosan egy (x,y) megoldáspárja legyen. Ekkor ezzel az "a" értékkel kiszámolva az (x,y) megoldáspárt, a kapott képlet alapján a metszéspont szerkeszthető.
Mi van, ha az "e" ellipszis úgy érinti a "k" kört, hogy a kör az ellipszis belsejében van.
Ez a probléma felkeltette az érdeklődésemet, még fogok vele foglalkozni. bertalan Zoltán.
|
| Előzmény: [1859] Bagesz, 2014-09-15 04:52:30 |
|
| [1868] Bátki Zsolt | 2014-09-23 18:19:23 |
 Az a sejtésem, hogy általánosságban euklidészi módon nem szerkeszthető. Ehhez találni kellene, egy elrendezést, amit algebrailag megoldva olyan szakasz jön ki, ami bizonyítottan nem szerkeszthető. pl köbgyök. A geogebra megenged pl szögharmadolást is ami eukledészi módon bizonyítottan nem megy. Az inverzió jó ötletnek tűnik. A feladat szépsége, hogy annyira egyszerű a felvetés, hogy érthetetlen evvel nem foglalkozott Senki, vagy mi nem tudunk róla ?
|
|
| [1867] Hajba Károly | 2014-09-19 20:31:37 |
 Erre azóta én is rájöttem. De ettől függetlenül a megoldást nagy valószínűséggel az inverzión keresztül lehet megtalálni.
Egy CAD-es programmal én is próbálok jó szerkesztést találni. A két pont és a tükörpont egy kört ad és az AB szakasz szakaszfelező merőlegese ill. a tükrözési tengely egy negyedik pontként ugyanezen körön metszik egymást. Pl az A és B pontot összekötő egyenes ill. az AB szakasz szakaszfelező merőleges inverziókörei alapján ezen kör inverziókörének két pontja már adott. Csak egy harmadik ismert pontra nem lelek rá.
|
| Előzmény: [1866] Bagesz, 2014-09-18 21:31:54 |
|
| [1866] Bagesz | 2014-09-18 21:31:54 |
 Szia! Jó ötletnek tűnt ezért utána jártam a szerkesztésének. GeoGebrával el is készítettem, de sajnos nem a kívánt pontban metszette a kört. További ötleteket szívesen várok. Üdv, Bagesz
|
 |
| Előzmény: [1864] Hajba Károly, 2014-09-16 17:17:55 |
|
| [1865] Bagesz | 2014-09-16 22:26:02 |
 A bizonyítás egyszerű, "A" és "B" pont közé kifeszítünk egy kötelet, ami kicsit hosszabb mint az "A" és "B" pont közötti távolság, Majd húzunk egy görbét úgy hogy feszes legyen a kötél mindvégig. Ez egy elipszis lesz. Majd egyre nagyobb kötelet veszünk, egyszer csak érinteni fogjuk a kört. Ez a pont a megoldás. Ezen a ponton az elipszis érintője és a két fókuszpontja által bezárt szög megegyezik, mint ahogy bármelyik pontja az elipszisnek és a két fókuszpontjával összekötő egyenes által bezárt szög.
|
 |
| Előzmény: [1860] Bátki Zsolt, 2014-09-15 22:28:23 |
|
| [1864] Hajba Károly | 2014-09-16 17:17:55 |
 Nem vagyok jártas a témában, de talán inverzióval (körre történő tükrözéssel) lehet a megoldást megtalálni.
Ki kellene próbálni, hogy az egyik pontot invertáljuk a körre és összekötjük a másikkal. Lehet, a metszéspont adja a megfelelő pontot a köríven.
|
| Előzmény: [1859] Bagesz, 2014-09-15 04:52:30 |
|
| [1863] Bátki Zsolt | 2014-09-16 13:57:23 |
 Bocsánat. Jó ötletnek tűnt. Jó, hogynem kezdtem el bizonyítani. A majdnem jó megoldás visz el igazán a lényegtől.
|
|
|
| [1861] Bátki Zsolt | 2014-09-15 22:32:53 |
 Persze a C nem az O a kör középpontja. Elírtam, de remélem értitek.
|
|
| [1860] Bátki Zsolt | 2014-09-15 22:28:23 |
 Ha a két pont egyenese közrefogja a kört, akkor annak egyenese kimetszi a megoldást a körből.(háromszög egyenlőtlenség) AB>=AP+PB Ha AB szakasz kívül van a körön, akkor rajzoljunk egy szabályos háromszöget a körhöz képest kifelé. Ennek csúcspontja C. C és a kör középpontja O által meghatározott egyenes és a kör metszéspontja a nyerő. P pont. Nem tudom bizonyítani, de Geogebrával ellenőrizhető. Valószínűleg köze van ahhoz, hogy egy 120 fokosnál kisebb háromszög esetén AP+BP+CP összeg akkor a legkisebb, ha P minden oldalról 120 fokos szögben látszik. (Nem tudom kinek a tétele)
Így a szerkesztés nagyon egyszerű. Köszönöm a feladatot. megj, Fizika: a fény a legrövidebb utat keresi. Tehát ha tükörből van a kör (henger) akkor A-ból a B pontot P pontban látjuk. (Beesési és kimenő szög egyenlő) Aki akarja bizonyítsa, hogy tényleg ez a minimális. Érdekel a megoldás.
|
|
| [1859] Bagesz | 2014-09-15 04:52:30 |
 Sziasztok! Két pont között a legrövidebb utat kellene kiszámolnom, úgy hogy egy kört kell érinteni. Ismert a 2 pont és a kör koordinátái, valamint a kör sugara. Azt tudom, hogy a kör azon pontja a keresett pont, ahol a kör érintője és a pontok által bezárt szög megegyezik. Ezt viszont hogy lehet kiszámolni vagy kiszerkeszteni? Előre is köszi a segítséget. Üdv
|
 |
|
|
| [1857] Sinobi | 2014-08-10 20:25:29 |
 ennek kupszeletes altalanositasarol tudsz valamit? igaz-e, hogy 4-5 kupszelethez mindig letezik olyan kupszelet, amely mindegyiket erinti?
-
@w: "Legyen ABC háromszög BC oldalához írt köre h, amely a BC oldalt D-ben érinti. Tekintsük azt a k kört, amely áthalad a B és C pontokon, és érinti h-t (de nem a BC egyenes). Mutassuk meg, hogy h és k érintési pontját P-vel jelölve, PD egyenes felezi a BPC szöget."
Vesszuk BC Apolloniusz-korei kozul azt, amelyik meroleges h-ra. Athalad P-n es D-n, mert invertalva ra P es D fixen kell maradjanak.
|
| Előzmény: [1856] Fálesz Mihály, 2014-08-08 16:56:22 |
|
| [1856] Fálesz Mihály | 2014-08-08 16:56:22 |
 Ez az Apollóniusz féle szerkesztési feladat speciális esete: adott három kör, pont vagy egyenes, szerkesszünk olyan kört, ami mindhármat érinti (pont esetén átmegy rajta).
Egy tipikus megoldás, hogy a körök sugarait ugyanannyival megváltoztatjuk úgy, hogy az egyik kör ponttá fajuljon. (Az egyenest eltoljuk). Ezután jöhet egy inverzió, ami visszavezeti a feladatot két kör közös érintőinek megszerkesztésére.
|
| Előzmény: [1855] djuice, 2014-08-08 15:07:32 |
|
| [1855] djuice | 2014-08-08 15:07:32 |
 Sziasztok!
Az alábbi geometriai szerkesztési példán gondolkodom már napok óta, de nem jutok eredményre. Tudnátok segíteni?
Adottak "r1" és "r2" tetszőleges sugarú és helyzetű körök a síkon, valamint egy őket nem érintő és nem metsző "f" egyenes, melynek ismerjük a körök középpontjától mért paraméteres (n1-; n2-szeres) távolságát. Szerkesszük meg azt a közbeeső kört, mely érinti mindkét kört és az egyenest! Számítani is próbálom a pontokat, de a szerkesztés volna a lényeg.
Mellékelem az ábrát is:
|
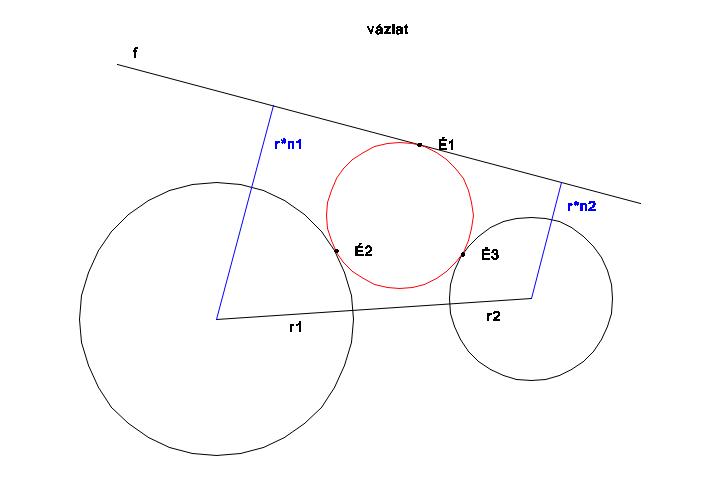 |
|
|
| [1853] csábos | 2014-07-18 09:22:53 |
 Tekintsük azt a tetraédert, amely alapja az &tex;\displaystyle ABC&xet; háromszög és minden lapja egybevágó vele. Másképp: Induljon ki az &tex;\displaystyle A&xet; csúcsból egy &tex;\displaystyle a&xet; hosszú, a &tex;\displaystyle B&xet; csúcsból egy &tex;\displaystyle b&xet; hosszú, a &tex;\displaystyle C&xet; csúcsból egy &tex;\displaystyle c&xet; hosszú él. Ekkor a keresett pont a &tex;\displaystyle D&xet; csúcsból induló magasság talppontja.
MOTIVÁCIÓ: Oldjuk meg a feladatot térben. Ha a &tex;\displaystyle P&xet; (síkbeli pont) olyan, hogy a &tex;\displaystyle Q&xet; vetülete az &tex;\displaystyle ABC&xet; síkra &tex;\displaystyle P&xet;, akkor &tex;\displaystyle QA^2=PA^2+QP^2&xet;, ugyanez szimmetrikusan. Így a &tex;\displaystyle QBC&xet; háromszög oldalainak négyzetösszege &tex;\displaystyle 2QP^2&xet;-tel nagyobb, mint a &tex;\displaystyle PBC&xet;-é. A fent leírt &tex;\displaystyle D&xet; pont nyilvánvalóan teljesíti a feltételeket. Az, hogy nincs másik, az is kijön. Ha a &tex;\displaystyle P'&xet; pont jó, akkor emeljük ki a síkból olyan ,,magasra", hogy a keresett összeg épp &tex;\displaystyle a^2+b^2+c^2&xet;. Ekkor a feltételeket felírva adódik, hogy &tex;\displaystyle |Q'A|=a&xet;.
Síkban úgy oldanám meg, hogy keresném a &tex;\displaystyle P&xet; pont &tex;\displaystyle X&xet; tükörképét mondjuk az &tex;\displaystyle AC&xet; oldal felezőpontjára. Ekkor a &tex;\displaystyle PBC&xet; és &tex;\displaystyle PAB&xet; háromszögekre felírt négyzetösszegből &tex;\displaystyle PB^2&xet;-t kivonva &tex;\displaystyle XC^2+AB^2=XA^2+BC^2&xet; adódik, azaz a &tex;\displaystyle BCXA&xet; négyszög átlói merőlegesek. Innen az említett módokon adódik a &tex;\displaystyle P&xet; pont heyzete.
|
| Előzmény: [1852] w, 2014-07-17 18:56:13 |
|
| [1852] w | 2014-07-17 18:56:13 |
 OK igen.
Van egy analóg vektoros megoldás, azt a megoldást vártam (bár én tipikusan koordinátázom a feladatokat). Vagyis ha most a kisbetűk a megfelelő csúcsokhoz tartozó vektorok, akkor a feltétel szerint
&tex;\displaystyle (a-b)^2+(b-x)^2+(x-a)^2=(a-c)^2+(c-x)^2+(x-a)^2&xet;
és ennek ciklikus permutáltjai állnak fenn. Előbbi egyenletet kicsit alakítva, kapjuk, hogy (skalárszorzatokkal)
&tex;\displaystyle [(a^2-2ab+b^2)-(a^2-2ac+c^2)]+[(b^2-2bx+x^2)-(c^2-2cx+x^2)]=0,&xet;
&tex;\displaystyle 2(-a+b+c-x)(b-c)=0,&xet;
azaz &tex;\displaystyle \vec{AB}+\vec{XC}&xet; vektor merőleges &tex;\displaystyle BC&xet;-re. Előbbi vektor &tex;\displaystyle A&xet;-ból az &tex;\displaystyle X&xet; pont &tex;\displaystyle BC&xet; felezőpontjára vett tükörképébe mutat, vagyis &tex;\displaystyle X&xet; rajta van az &tex;\displaystyle A&xet;-ból induló magasság &tex;\displaystyle BC&xet; felezőpontjára vonatkozó tükörképén. Hasonlóan, a &tex;\displaystyle B&xet;-ből és &tex;\displaystyle C&xet;-ből induló magasságok tükörképein is rajta van. Az egyetlen ilyen pont a kiegészítő háromszög magasságpontja.
Jellegétől fogva a feladatot szerintem nem nagyon lehet koordináták/vektorok nélkül megoldani. Kíváncsi vagyok, hogy mégis van-e "elemi" megoldása.
|
| Előzmény: [1851] emm, 2014-07-17 13:09:23 |
|
| [1851] emm | 2014-07-17 13:09:23 |
 &tex;\displaystyle x=a+b&xet; épp a magasság oldalfelező merőlgesre vett tükörképe, a koordinátázás meg oldalfüggetlenül szimmetrikus, szóval mind a 3 ilyen egyenesen rajta van, ebből meg kb. adódik a sejtés, hogy így lehetne értelmezni.
|
| Előzmény: [1850] w, 2014-07-17 12:49:11 |
|
