| [331] Chryst | 2006-01-08 10:59:05 |
 Jézusom!!!
Megvan a megoldás!!! És nagyon egyszerű. Csak nem értem, hogy eddig egyedül, magamtól hogy nem jöttem rá.
Leírom:
(x-u)2+(y-v)2=r2
rendezgetek egyet:
(x-u)2=r2-(y-v)2
gyököt vonok:

megint rendezkedek, és már ki is derül milyen apróság nem jutott eddig eszembe:

Hát igen, ismételten beigazolódott: "Az igazi zseniknek a legegyszerűbb dolgok jelentik a legnagyobb problémát" :)
A segítséget azért köszönöm
|
|
| [330] Chryst | 2006-01-08 10:21:14 |
 Köszönöm, de ilyesmiket én is kihoztam, csak mindegyikkel ugyanaz az egy baj volt:
x2-2xu+u2+(y-v)2-r2=0
Ebből ugyebár ezt kapom:
x2=2xu-u2-(y-v)2+r2 vagy x2-2xu=r2-u2-(y-v)2
Ez nekem azért rossz, mert ha én a programmal az x-et akarom kiszámoltatni, akkor az x csak egyszer szerepelhet az egyenletben, méghozzá x=? helyen.
Ezekben az egyenletekben szerintem első problémát az jelenti, hogy az egyik x előtt van egy u szorzó. Megpróbáltam eltenni máshová azt az u-t, de akkor meg az x2 alá került, valahogy így:

és ez nekem már megint nem jó, mert onnan az x2-et még annyira sem tudom kivenni.
Lényegében nekem egy olyan egyenlet kell, mint amit akkor csinálunk, amikor több ismeretlenes egyenleteket számoltunk azzal a módszerrel, hogy az egyik ismeretlent kifejezem, amit meg kapok, azt behelyettesítem a másik egyenletbe. Amikor így fejezem ki az egyik ismeretlent, akkor nem szerepelhet a másik oldalon is az az ismeretlen, mert akkor nem tudnám kiszámolni a másik ismeretlent.
Szóval nekem egy ilyen egyenletre (vagy inkább képletre) lenne szükségem.
Nem akarok kört rajzolni, csak azt akarom megvizsgáltatni, hogy egy, a képernyőn elhelyezkedő pont egy bizonyos (előre megadott) körön belül van-e. Szóval szerintem mindenféleképpen ezzel az egyenlettel célszerű számolnom.
Tudom, hogy ezzel a képlettel még csak egy kör körvonalát kapom meg, de egyelőre még nem akartam egyenlőtlenséggel számolni, (ezzel: (x-u)2+(y-v)2<r2) mert ezzel ráérek majd akkor foglalkozni, amikor a progit írom. Ha egy kör körvonala megvan, az már fél siker, kiindulásnak elég lesz.
A további segítségeket előre is köszönöm
|
| Előzmény: [329] 2501, 2006-01-08 02:59:52 |
|
| [329] 2501 | 2006-01-08 02:59:52 |
 (x-u)2+(y-v)2=r2
x2-2xu+u2+(y-v)2-r2=0
Innen mar remelem megy egyedul is. :)
(Lesz benne gyokvonas. Ha kort kell rajzolni, akkor vannak ennel sokkal hatekonyabb eljarasok.)
|
| Előzmény: [328] Chryst, 2006-01-07 22:19:47 |
|
| [328] Chryst | 2006-01-07 22:19:47 |
 Programozok, és egy programban szeretnék kipróbálni valamit, amihez (koordináta geometriában) a kör egyenletéből ki kellene fejeznem az x-et, de egyedül nem tudok értelmes (aránylag egyszerűnek mondható) választ csinálni az "x=?" kérésre... Sőt! Egyáltalán nem tudok semmit kihozni x-re. Ha valaki segítene, annak nagyon örülnék.
Előre is nagyon köszönöm.
Ha valaki segítene, de hirtelen nem jut eszébe az egyenlet, annak mellékeltem ábraként. (A körvonal bármely P(x;y) pontja C(u;v) középponttól adott r távolságra van.) (Csakhogy precízek legyünk :)
Mégegyszer köszönöm.
|
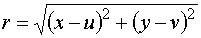 |
|
| [327] Iván88 | 2006-01-06 15:20:39 |
 Ez van. Ez a sejtés nem jött be. (Közben én is rájöttem, a koszinusz-tételből) Pedid olyan szépen hangzott :-(
A matemetikus halála az, amikor egy szép sejtést tönkretesz egy csúnya tény.
|
| Előzmény: [326] jonas, 2006-01-06 13:28:16 |
|
| [326] jonas | 2006-01-06 13:28:16 |
 Nem igaz.
Egyrészt azért, mert ha a b, akkor a paralellogrammát lapítva az átlók által bezárt szög is akármilyen lapos lehet. b, akkor a paralellogrammát lapítva az átlók által bezárt szög is akármilyen lapos lehet.
Másrészt ha a paralellogramma két szomszédos csúcsát rögzíted, és a másik kettőt mozgatod (úgy, hogy az oldalhosszak rögzítettek), akkor a középpont egy körön mozog. Az átlók szöge akkor lenne állandó, ha ez a kör a rögzített oldal egy látóköre lenne, de nem az, mert a középpont nem megy a rögzített csúcsok közelébe.
|
| Előzmény: [325] Iván88, 2006-01-05 15:58:13 |
|
| [325] Iván88 | 2006-01-05 15:58:13 |
 Igaz e, hogy az adott a, b oldalú paralelogrammákban (nem rombusz) az átlók által bezárt szög állandó? (a, b rögzített érték, az oldalak szögét változtatjuk.)
|
|
|
|
| [322] philip | 2005-12-03 22:25:32 |
 Hogyan bizonyítjuk a Fauerback-kört (kilencpont-köre)?
|
|
| [321] Róbert Gida | 2005-11-30 20:30:07 |
 63. feladat
Adott a síkon egy kör, melyek azok a legkisebb területű ellipszisek, melyek tartalmazzák a félkört? Igaz-e hogy az ellipszis területe kisebb, mint a kör területe?
Az egyszerűsítések érdekében feltehetjük, hogy a kör és az ellipszis középpontja ugyanazon a koordináta-tengelyen van és az ellipszis megfelelő tengelyei párhuzamosak a koordináta-tengelyekkel.
Ugyanez a kérdés magasabb ( n ) dimenzióban. Melyek azok az n dimenziós ellipszoidok melyek tartalmazzák az n dimenziós félgömböt, úgy hogy az ellipszoid térfogata minimális legyen, ez a térfogat kisebb-e mint a gömb térfogata? Ugyanazon egyszerűsítéseket most is feltehetjük mint előbb a tengelyekre vonatkozóan.
|
|
|
| [319] lorantfy | 2005-11-30 09:14:39 |
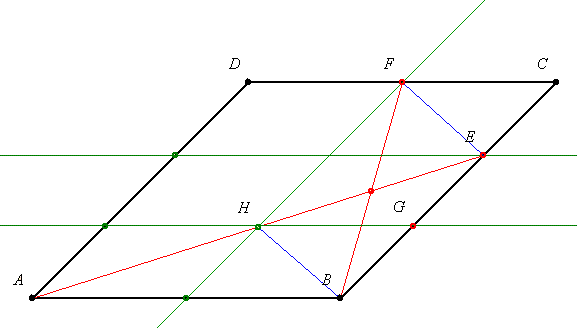
 A legprimitívebb módszer, hogy párhuzamosokat húzunk a felező és harmadoló pontokból az oldalakkal. AE felezőpontja H. Aztán BEFH paralelogramma átlói felezik egymást.
|
 |
| Előzmény: [318] philip, 2005-11-29 19:51:23 |
|
| [318] philip | 2005-11-29 19:51:23 |
 Köszönöm szépen a segítséget! Lenne mégegy feladatom: Az ABCD négyszög paralelogramma,amelynek BC oldalát az E pont harmadolja úgy,hogy E C-hez van közelebb,az F pedig a DC oldalt felezi.Bizonyítsuk be,hogy a BF szakasz az AE szakaszt negyedeli,az AE a BF szakaszt felezi!
|
|
| [317] jonas | 2005-11-24 10:11:26 |
 Hmm. A 18 tényleg rossz.
Akkor x=1/(1/b+1/c)=8.
Ez onnan jön ki, hogy az FEC és a DBE háromszög hasonló az ABC-hez, mert az oldalaik párhuzamosak, így aztán a CE szakasz ax/c, az EB szakasz ax/b, amiből a=ax/c+ax/b.
|
| Előzmény: [316] lorantfy, 2005-11-24 08:11:52 |
|
|
|
| [314] philip | 2005-11-23 17:43:45 |
 Sziasztok! Az alábbi feladat megoldásában szeretnék segítséget kérni:
1.Egy háromszög oldalainak hossza c=24 a=18 b=12.Írjunk bele olyan rombuszt,amelynek egyik csúcsa az A,a többi csúcsa a háromszög oldalaira illeszkedik.
Eéőre is köszönöm!
|
|
| [313] nadorp | 2005-11-22 12:09:49 |
 Azt hiszem van valami a szimplexre. Először belátunk egy állítást:
Legyenek a,b,c pozitív számok, min(a,b,c)=a, b c Ekkor léteznek olyan x,y,z pozitív számok,hogy x<a, c Ekkor léteznek olyan x,y,z pozitív számok,hogy x<a,
x+y+z=a+b+c
x2+y2+z2=a2+b2+c2,továbbá xyz<abc is teljesül. Biz:
Az egyenletrendszer ekvivalens az alábbival ( ):
y+z=a+b+c-x
y2+z2=a2+b2+c2-x2,azaz
yz=x2-(a+b+c)x+(ab+ac+bc).
Egy kis számolással adódik, hogy a fenti egyenletrendszer olyan másodfokú egyenletre vezet, melynek diszkriminánsa b c esetén alkalmas x<a-ra pozitív,ezért a fenti egyenletrendszernek létezik ezzel az x-szel y,z pozitív megoldása.Már csak az abc>xyz egyenlőtlenséget kell belátni. c esetén alkalmas x<a-ra pozitív,ezért a fenti egyenletrendszernek létezik ezzel az x-szel y,z pozitív megoldása.Már csak az abc>xyz egyenlőtlenséget kell belátni.
xyz=x3-(a+b+c)x2+(ab+ac+bc)x=f(x). Mivel f(0)=0 és f(a)=abc, ezért ha bebizonyítjuk, hogy f(x) a [0,a]-n monoton, akkor kész vagyunk. Ehhez elég belátni, hogy a derivált függvény gyökei nagyobb egyenlőek, mint a. Ez egy kis számolással a (b-a)(c-a) 0 nyilvánvaló egyenlőtlenségre vezet. 0 nyilvánvaló egyenlőtlenségre vezet.
Az eredeti feladat ezek után egyszerű. Ha
 és és
 , akkor , akkor
 ,ebből ,ebből
xn 1- 1- . A fenti állításból következik, hogy a koordináták szorzata akkor minimális, ha valamelyik xi éppen 1- . A fenti állításból következik, hogy a koordináták szorzata akkor minimális, ha valamelyik xi éppen 1- , a többi pedig egyenlő.Ez viszont nem lehet más,mint , a többi pedig egyenlő.Ez viszont nem lehet más,mint 
|
|
| [312] Lóczi Lajos | 2005-11-21 20:35:48 |
 Eddig mi már beláttuk az a.) pontot, sőt annál többet is: a szorzat a minimumot/maximumot olyan pontokban veszi fel (és nem csak "veheti"), ahol az xi számok pontosan 2 különböző értéket vesznek fel, l. a Lagrange multiplikátoros (valamint kompaktsági) érvelést.
A b.) rész n=3-ra a [302]-es hozzászólás-beli utolsó képletemből szinte triviális, két polinomot kell összehasonlítani, a k=2 érték minden  >0 esetén kisebb, mint a k=1-hez tartozó. >0 esetén kisebb, mint a k=1-hez tartozó.
Hiányzik a c.) rész, valamiféle induktív érvelés kellene tehát. Ha ez meglenne, akkor
ezek alapján a d.) kérdésre is pozitívan válaszoltunk.
Mindenesetre rögtön adódott egy szép és nehéz egyenlőtlenség a [302]-es végéről. Ha n nagy, akkor annak a függvénynek a képe "kotangens" jellegű, ilyen típusú függvényekről pedig tudom, hogy meggyűlt velük már a bajom :)
|
| Előzmény: [311] Róbert Gida, 2005-11-21 19:49:09 |
|
| [311] Róbert Gida | 2005-11-21 19:49:09 |
 Nem úgy látom be, segítség a 61. feladathoz:
62. feladat
a. Legyen a és b rögzített pozitív valós számok és n>1 pozitív egész, ahol  . Legyen . Legyen  és és  ,x=(x1,x2,...,xn) ,x=(x1,x2,...,xn) 0 , akkor 0 , akkor  a minimumot olyan pontban veheti csak fel, ahol az xi-k pontosan két különböző értéket vesznek fel. a minimumot olyan pontban veheti csak fel, ahol az xi-k pontosan két különböző értéket vesznek fel.
b. Bizonyítsuk be, hogy n=3-ra a minimumot olyan pontban veszi fel, ahol 2 darab xi megegyezik, a külöböző pedig kisebb.
c. Bizonyítsuk be n>3-ra, hogy a minimumot olyan pontban veszi fel, ahol (n-1) darab xi megegyezik, a különböző pedig ettől kisebb.
d. Ezzel bebizonyítottuk-e a 61. feladatot?! Ha igen akkor miért?
|
| Előzmény: [310] Lóczi Lajos, 2005-11-21 13:08:17 |
|
| [310] Lóczi Lajos | 2005-11-21 13:08:17 |
 Legalább már "látjuk" a kontextust, de ezzel nem jutottunk közelebb a megoldáshoz :)
Azt kérdezném még, hogy be tudnád-e látni a [302]-es hozzászólás végén szereplő kifejezésről, hogy k-ban szigorúan monoton fogy (vagy várom a másik utat, hogy anélkül hogyan tudjuk minimalizálni a szorzatot...)
|
| Előzmény: [309] Róbert Gida, 2005-11-21 07:11:15 |
|
| [309] Róbert Gida | 2005-11-21 07:11:15 |
 Ez a lineáris programozási feladatnak Karmarkar féle projektív módszeréhez kell ez az állítás. Konkrét tétel ( neve is van ) ez az állítás a projektív módszernél. Projektív módszer egy polinomiális futás idejű algoritmus, ellentétben a szimplex módszerrel a lineáris programozási feladatokra. Módszer lényege, hogy trafókkal eléri, hogy min(x1) ahol  -t kell meghatározni, tehát pont a mi szimplexünkőn dolgozik, egy hipersíkkal elmetszve, ráadásul úgy, hogy egy lépésben ezt az -t kell meghatározni, tehát pont a mi szimplexünkőn dolgozik, egy hipersíkkal elmetszve, ráadásul úgy, hogy egy lépésben ezt az  *r sugarú gömböt is használva egy kisebb x1 értékkel rendelkező megengedett megoldást talál és úgy transzformálja a feladatot, hogy újra ebbe a szimplexbe viszi a feladatot ( az A más lesz ) a megengedett megoldást pedig a gömb középpontjába, ami a csupaegy vektor. *r sugarú gömböt is használva egy kisebb x1 értékkel rendelkező megengedett megoldást talál és úgy transzformálja a feladatot, hogy újra ebbe a szimplexbe viszi a feladatot ( az A más lesz ) a megengedett megoldást pedig a gömb középpontjába, ami a csupaegy vektor.
Ha kell akkor tovább bontom a feladatot.
|
| Előzmény: [308] Lóczi Lajos, 2005-11-20 19:34:22 |
|
| [308] Lóczi Lajos | 2005-11-20 19:34:22 |
 Az extremizálandó xi-szorzatnak szerintem az az érdekessége (és ez ellentmond a szemléletnek), hogy éppen akkor lesz minimális, ha a lehető legtöbb szám egynél nagyobb benne és csak 1 db lesz 1-nél kisebb; illetve akkor maximális az értéke, ha (n-1) db kisebb 1-nél és csak 1 db nagyobb 1-nél közülük.
Majd megkérdezzük Róbert Gidát, hogy honnan szedte ezt a feladatot, biztosan nem "csak úgy" kitalálta :)
|
| Előzmény: [307] nadorp, 2005-11-20 18:59:58 |
|
|
| [306] Lóczi Lajos | 2005-11-20 18:53:07 |
 [A Lagrange-multiplikátoros módszerhez a teljesség kedvéért hozzá kell tenni, hogy ugye ott lehetnek szélsőértékpontok, ahol a célfüggvény és a feltételi függvények deriváltjainak (multiplikátorokkal vett) lineáris kombinációja a nullvektor, VAGY OTT, ahol a feltételi függvények deriváltvektorai lineárisan összefüggenek. Nem egy tankönyvet láttam már, ahol ez utóbbi eshetőséget elfelejtették a példamegoldások során külön megvizsgálni (és így bizonyos, erre kihegyezett példákat nem is jól oldanának meg). A mi esetünkben ez az eset azért nem fordulhat elő, mert ahol lineáris függőség van, azok a pontok nincsenek a hipergömb felületén.
Aztán a másik apróság, hogy azt mondtuk: az xi-k egy másodfokú egyenlet megoldásai. Azonban a másodfokú egyenlet csak elsőfokú, ha az egyik multiplikátor éppen nulla lenne. Ekkor minden xi azonos lenne, de ez is ellentmondást adna a feltételi egyenletekkel.]
|
| Előzmény: [305] Lóczi Lajos, 2005-11-20 18:37:23 |
|
| [305] Lóczi Lajos | 2005-11-20 18:37:23 |
 Na igen, kétféle értéket vehetnek fel az xi-k, ez igaz, az egyik értéket vegye fel k darab, a másik értéket (n-k) db (k=1,2,3,...,n-1; mind egyforma nem lehet, ezt könnyű látni). Ezeket behelyettesítve a két eredeti feltételi egyenletünkbe (t.i. az xi pontok a hipergömbfelületen és a hipersíkon is rajta vannak) megkapjuk, mi is lehet az a kétféle érték, ez az amit Te u-val és v-vel jelöltél.
Azonban u és v is függ k-tól! Tehát az Általad leírt egyenlőtlenséglánc egyáltalán nem látszik, és ez az a pont, ahol nekem is csak numerikus kísérleteim vannak.
|
| Előzmény: [304] nadorp, 2005-11-20 17:31:44 |
|
| [304] nadorp | 2005-11-20 17:31:44 |
 Hülyeséget írtam, nem xi= xj , hanem arra gondoltam, amire Te,hogy ebből némi esetszétválasztással kétféle érték adódhat az xikre. A vége változatlan. xj , hanem arra gondoltam, amire Te,hogy ebből némi esetszétválasztással kétféle érték adódhat az xikre. A vége változatlan.
|
| Előzmény: [303] nadorp, 2005-11-20 17:17:53 |
|
| [303] nadorp | 2005-11-20 17:17:53 |
 Én ezt csináltam,de találtam valamit. Ha a Lagrange multiplikátor módszerrel dolgozol, akkor pld:
x1x2..xn-1=2axn+b. Mivel xn>0,ezért szorozhatunk vele
x1...xn=2axn2+bxn, azaz
2axi2+bxi=2axj2+bxj, amiből következik, hogy xi= xj. Tehát a számok csak kétféle értéket vehetnek fel.Legyen ez a két érték u és v. Ekkor ha pld. u>v, akkor xj. Tehát a számok csak kétféle értéket vehetnek fel.Legyen ez a két érték u és v. Ekkor ha pld. u>v, akkor
uvn-1<u2vn-2<u3vn-3<...<un-1v miatt szélsőérték csak ott lehet, ahol az egyik szám egyszer, másik (n-1)-szer szerepel.
|
| Előzmény: [302] Lóczi Lajos, 2005-11-20 15:25:56 |
|
| [302] Lóczi Lajos | 2005-11-20 15:25:56 |
 A pontosság kedvéért hozzá kell tennem, hogy az én bizonyításom sajnos nem teljes.
Lagrange-multiplikátorokkal némi meggondolás (és esetszétválasztás) után kiadódnak azok a pontok, ahol a szorzatnak szélsőértéke lehet: k db xi azonos az  számmal és (n-k) db azonos az számmal és (n-k) db azonos az  értékkel, ahol k=1,2,...,n-1. értékkel, ahol k=1,2,...,n-1.
A gömb azonban kompakt és a függvény folytonos, ezért létezik minimum és maximum, tehát a fenti pontok között ott van a szorzat minimuma és maximuma.
A numerikus kísérletek szerint k=1-nél lesz a maximum, és k=n-1-nél a minimum, de ezt nem tudtam pár óra alatt belátni (több időt pedig nem tudok rászánni egyelőre). Elég lenne bebizonyítani, hogy a

függvény monoton fogyó a lehetséges k értékekre, a lehetséges n és  paraméterértékek mellett, de ez így nem tűnik egyszerűnek. paraméterértékek mellett, de ez így nem tűnik egyszerűnek.
Te milyen módszerrel jutottál túl ezen a ponton (ha egyáltalán ilyesféleképp csináltad)?
|
| Előzmény: [301] nadorp, 2005-11-20 13:34:19 |
|
|
| [300] Lóczi Lajos | 2005-11-19 20:27:52 |
 Nyilván csak 0< <1 vizsgálata szükséges. <1 vizsgálata szükséges.
Láttuk, hogy  =1 esetén valamelyik xi-nek 0-nak kell lennie, hogy a szorzat minimális legyen. Az is leolvasható az adott bizonyításból, hogy ha =1 esetén valamelyik xi-nek 0-nak kell lennie, hogy a szorzat minimális legyen. Az is leolvasható az adott bizonyításból, hogy ha  >0, akkor minden xi>0 kell legyen, hogy a gömbfelületen maradjunk. >0, akkor minden xi>0 kell legyen, hogy a gömbfelületen maradjunk.
A megoldás a 61. feladatra az lesz, hogy az adott gömbfelületen elhelyezkedő xi számok (i=1,2,...,n) szorzata pontosan akkor minimális, ha közülük valamely (n-1) db egyenlő az  számmal, továbbá 1 darab közülük egyenlő (1- számmal, továbbá 1 darab közülük egyenlő (1- )-val. A minimum értéke ebből már meghatározható. )-val. A minimum értéke ebből már meghatározható.
Másrészt, ez ugyan nem volt kérdés, de az xi számok (i=1,2,...,n) szorzata pontosan akkor maximális, ha közülük valamely (n-1) db egyenlő az  számmal, továbbá 1 darab egyenlő (1+ számmal, továbbá 1 darab egyenlő (1+ )-val. )-val.
|
| Előzmény: [299] Róbert Gida, 2005-11-18 15:54:44 |
|
|
| [298] nadorp | 2005-11-18 09:19:59 |
 a) Legyen e1=(n,0,0,...,0),e2=(0,n,0,...,0)...,en=(0,0,...,n). Ekkor az ei pontok nyilván egy szabályos (n-1) dimenziós S szimplexet határoznak meg. Ha x=(x1,x2,...,xn) eleme ennek a szimplexnek, akkor
 , ahol , ahol  , azaz , azaz  és xi és xi 0. Fordítva, ha 0. Fordítva, ha
 ,xi ,xi 0, akkor 0, akkor  és itt és itt  , azaz x eleme S-nek. Tehát a megoldáshalmaz egybeesik S-sel. , azaz x eleme S-nek. Tehát a megoldáshalmaz egybeesik S-sel.
b) Ha s a súlypont, akkor  , azaz, , azaz, 
c)Az n-dimenziós térben egy (n-1) dimenziós gömböt úgy kaphatunk,ha egy n-dimenziós gömböt elmetszünk egy (n-1) dimenzós síkkal. Ha P=(p1,p2,...,pn) a beírt gömb sugara, akkor szükségképpen S síkjában helyezkedik el,azaz  . Határozzuk meg P távolságát a szimplex (n-2) dimenziós lapjaitól, vegyük pld. a . Határozzuk meg P távolságát a szimplex (n-2) dimenziós lapjaitól, vegyük pld. a  lapot. Ekkor a (p1,...,pn-1,0) pontnak a laptól való távolsága lapot. Ekkor a (p1,...,pn-1,0) pontnak a laptól való távolsága  . Tehát P távolsága a laptól . Tehát P távolsága a laptól  . Ezt elvégezve az összes többi (n-2) dimenziós lapra és felhasználva, hogy ezek a távolságok egyenlőek kapjuk, hogy p1=p2=...=pn=1, azaz . Ezt elvégezve az összes többi (n-2) dimenziós lapra és felhasználva, hogy ezek a távolságok egyenlőek kapjuk, hogy p1=p2=...=pn=1, azaz  és a beírt gömb sugara és a beírt gömb sugara 
d) Nyilván, ha xi=0, akkor a szorzat 0, azaz minimális lehet.Megmutatjuk, hogy vannak ilyen pontok. Azt kell belátni, hogy pld. létezik x=(x1,x2,...,xn-1,0) pont úgy, hogy
 , xn=0 és , xn=0 és
 . .
A második egyenlőséget átrendezve felhasználva az elsőt:
 . Tehát . Tehát
 . Egyenlőség van, azaz . Egyenlőség van, azaz  . Hasonlóan kapjuk a többi n-1 darab pontot is. . Hasonlóan kapjuk a többi n-1 darab pontot is.
|
| Előzmény: [296] Róbert Gida, 2005-11-16 22:17:53 |
|
| [297] Róbert Gida | 2005-11-16 23:30:48 |
 60. feladat
Bizonyítsuk be vagy cáfoljuk meg:
A szabályos 30-szög belsejében pontosan 331 darab különböző olyan pont van, amin legalább 5 átló megy át.
|
|
| [296] Róbert Gida | 2005-11-16 22:17:53 |
 59. feladat
Legyen  az n dimenziós csupa 1 oszlopvektor. S legyen az az n dimenziós csupa 1 oszlopvektor. S legyen az  megoldáshalmaza. Bizonyítsuk be, hogy: megoldáshalmaza. Bizonyítsuk be, hogy:
a: Az S egy szabályos (n-1) dimenziós szimplex
b: Mi az S súlypontja?
c: Mi az S-be írható (n-1) dimenziós gömb középpontja és sugara?
d: Mennyi  ahol x=(x1,x2,...,xn) a beírható gömb felszínén van. A minimumot mely pontokban veszi fel? ahol x=(x1,x2,...,xn) a beírható gömb felszínén van. A minimumot mely pontokban veszi fel?
|
|
|
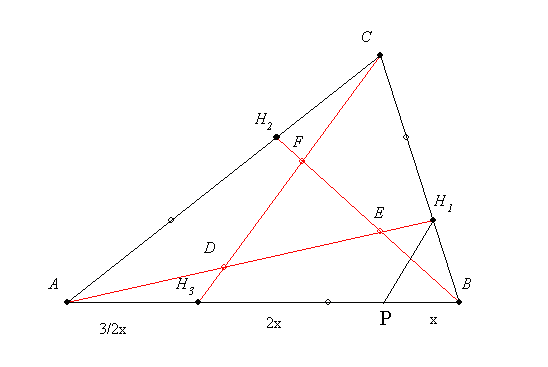
| [294] nadorp | 2005-11-15 15:01:25 |
 Jelentkező hiányában megróbálom. Húzzunk párhuzamost H1-ből CH3-mmal, ez az AB oldalt P-ben metszi.Ekkor ha PB=x, akkor a párhuzamos szelők tétele szerint H3P=2x és mivel H3 harmadoló pont,  . Az . Az  és és  háromszögek hasonlóak, a hasonlóság aránya az előbbiek szerint háromszögek hasonlóak, a hasonlóság aránya az előbbiek szerint  , így az AH3 és AP oldalakhoz tartozó magasságok aránya is ennyi.Ha m jelöli az AP-hez tarozó magasságot, akkor azt kaptuk, hogy , így az AH3 és AP oldalakhoz tartozó magasságok aránya is ennyi.Ha m jelöli az AP-hez tarozó magasságot, akkor azt kaptuk, hogy
 , azaz ha T jelöli az ABC háromszög területét, akkor , azaz ha T jelöli az ABC háromszög területét, akkor  . Hasonlóan ugyanez igaz a másik két kis háromszögre is. Másrészt ennek alapján . Hasonlóan ugyanez igaz a másik két kis háromszögre is. Másrészt ennek alapján  és ugyanez igaz a másik két keletkező négyszögre is. Összefoglalva és ugyanez igaz a másik két keletkező négyszögre is. Összefoglalva

|
 |
| Előzmény: [290] lorantfy, 2005-11-12 22:07:51 |
|
|
|
| [291] BohnerGéza | 2005-11-14 23:12:30 |
 58. feladat:
Az ABC háromszög beírt körének érintési pontjai A', B' és C', középpontja O, K az A'B'C' körülírt körének kp-ja.
Jelölje Ma az AC'B', Mb a BA'C' és Mc a CB'A' háromszög magasságpontját, valamint M az MaMbMc háromszög magasságpontját.
Legyen Oa az AC'B', Ob a BA'C' és Oc a CB'A' háromszög beírt körének középpontja, és K' az OaObOc körülírt körének kp-ja.
Bizonyítandó, hogy az O, a K, az M és a K' egybeesnek!
|
|
|
| [289] lorantfy | 2005-11-08 22:14:48 |
 A komplex számos megoldást itt a Fórumon is megtalálhatod a Felmerülő kérdések... témában Sirpi [143] hozzászólása. Ahogy az a megoldás, ez sem használja fel, hogy a szabályos háromszögek nem közös csúcsai egy körön vannak. Tehát elegendő annyit feltenni, hogy van egy közös csúcsuk.
|
 |
| Előzmény: [288] AzO, 2005-11-08 17:38:22 |
|
| [288] AzO | 2005-11-08 17:38:22 |
 Mostanaban kaptuk ezt a mackosajtos feladatot algebran, es komplex szamokkal (egyseggyokokkel) oldottuk meg, es mondta a tanar, hogy nem is akar belegondolni milyen nehez lenne elemi (kozepiskolai) modszerekkel megoldani :). Ennek ellenere ez frappans volt, es sztem megmutatom neki :) Koszi
|
| Előzmény: [287] lorantfy, 2005-11-06 12:04:50 |
|
| [287] lorantfy | 2005-11-06 12:04:50 |
 Tomszy feladata a Felmerülő kérdések ... témából:
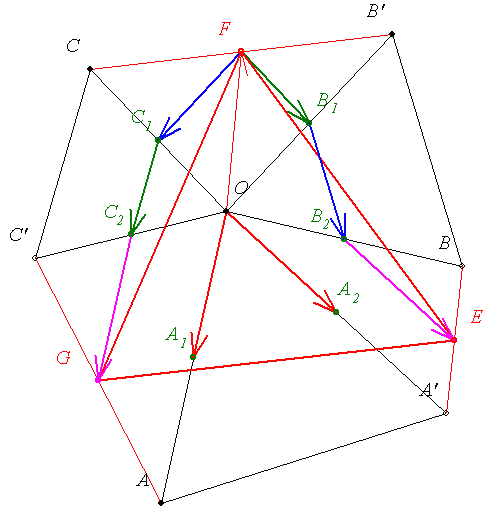
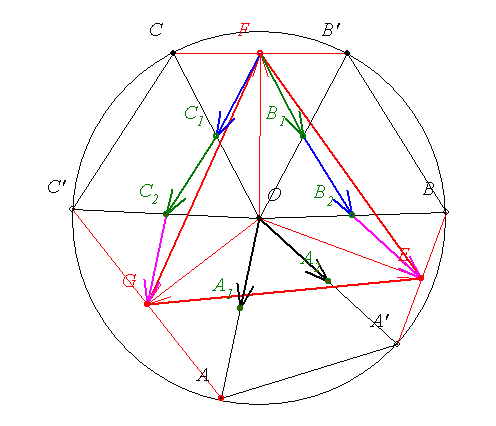
Egy r sugarú körben vegyünk fel három r sugarú húrt: AA', BB', CC'. Jelöljük A'B húr felezőpontját E-vel, B'C húr felezőpontját F-vel és C'A húr felezőpontját G-vel.
Bbh. EFG háromszög szabályos!
Megoldás vektorokkal: (Ugyanúgy megy mint a B.3837. feladat megoldása, amit a Lejárt határidejű ... témába írtam be.)
Legyenek A1,A2,B1,B2,C1,C2 a megfelelő, sugás hosszúságú szakaszok felezőpontjai.
A háromszög középvonalának tulajdonságai és a szabályos háromszögek miatt az ábrán azonos színnel jelölt vektorok egymásnak 60 fokos elforgatottjai.

Mivel a megfelelő összetevő vektorok egymás 60 fokos elforgatottjai, így  is 60 fokos elforgatottja is 60 fokos elforgatottja  -nek, tehát EFG -nek, tehát EFG szabályos háromszög. szabályos háromszög.
|
 |
|
|
| [285] Lóczi Lajos | 2005-09-20 13:59:13 |
 Jó, de nézd meg, hogy mi a könyv célja: könnyítést adni azoknak, akiknek nehezen megy, bizonyos területekre így kevesebb előismerettel is el lehet jutni -- persze onnan nem lehet olyan messzire továbbhaladni.
(Az elvi célja pedig inkább az, ahogy írja, hogy közben a geometriát nem kell a valós számok bonyolult fogalmára építeni: tetszőleges algebrai test is használható.)
|
| Előzmény: [284] Fálesz Mihály, 2005-09-20 11:35:29 |
|
| [284] Fálesz Mihály | 2005-09-20 11:35:29 |
 Én nem lelkesedek érte, sőt.
Trigonometria-feladatokban a szögeknek legfeljebb csak a szinuszát/koszinuszát szoktuk kiszámolni, magukat a szögeket nem. Négyzetgyökökkel pedig így is, úgy is számolni kell. Például elég megkérdezni, hogy ha az A,B,C pontok egy egyenesen vannak, mondjuk AB2=2 és BC2=3, akkor mekkora lehet AC2. A konstrukció csak a legegyszerűbb esetekben teszi félre a négyzetgyökvonást, a számolás egyáltalán nem lesz tőle sem könnyebb, sem egyszerűbb.
A trigonometrikus függvények elvetését pedig kb. olyan ötletnek tartom, mint ha valaki a prímszámtételből ki akarná irtani a logaritmust (mert hát ugye mi szükség van transzcendens függvényekre, ha egész számokról akarunk beszélni), vagy a Cardano-képletből a komplex számokat. Pont a matematikát akarja kiirtani; azt, hogy hozzunk létre elméleteket, új objektumokat (jelen esetben a trigonometrikus függvényeket), amik megmutatják, hogy a dolgok mögött milyen mélyebb összefüggések vannak.
F.M.
|
| Előzmény: [282] Lóczi Lajos, 2005-09-19 22:50:10 |
|
| [282] Lóczi Lajos | 2005-09-19 22:50:10 |
 Szép és elegáns a leírás, sokmindenben egyetértek vele, bár nem hiszem, hogy túlzottan nagy változást okozna mifelénk belátható időn belül, ha egy olyan alapvető fogalomhoz, mint a "szög" akar hozzányúlni, átdefiniálni.
|
| Előzmény: [281] 2501, 2005-09-19 10:25:15 |
|
|
|
| [280] Szalkai István | 2005-09-14 13:42:39 |
 Kedves Mindenki !
A 2005.jan. feladatot általánosítva jutott eszembe a a következő probléma: Mi azon pontok mértani helye, amelyeknek adott egyenesektől való távolságai kielégítenek egy lineáris összefüggést? "Felfedezésem" biztosan nem új, bár irodalomban nem akadtam a nyomára. Közzéteszem mégis, hátha esetleg valakinek hasznára válik, no és biztosan én is tanulok hozzászólásaitokból! (Más fajta TEX-et használva nem sikerült a szöveget ide feltennem, de a következő linken megtalálható:
http://www.szt.vein.hu/~szalkai/Tavolsagok-jav.pdf
Üdvözlettel: szalkai@almos.vein.hu
|
|
| [279] BohnerGéza | 2005-08-27 00:19:34 |
 Jogos [275] jonas észrevétele, bár csak egy kis fogalmazási hibát követtem el. A zárójel szövege helyesen: valamint a talpponti háromszög területének. Igaz ez már nem nehéz, ha az előzőekre megvan a válasz.
|
| Előzmény: [275] jonas, 2005-08-23 22:40:10 |
|
| [278] lorantfy | 2005-08-24 10:25:21 |
 Hello Viktor!
Ez az EUKLIDES program. A 2.02 verzió ingyenesen letölthető: www.euklides.hu.
Töltsd le és szórakozz el vele. Én a kész ábrát Print Screen-el vágólapra szoktam tenni. Aztán egy képszerkesztővek kivágom a lényeges részt és átlátszóvá teszem, majd elmentem gif-ben és úgy csatolom a hozzászóláshoz. Így a háttérszínen jelenik meg.
|
| Előzmény: [277] xviktor, 2005-08-24 10:09:36 |
|
|
|
|
| [274] BohnerGéza | 2005-08-23 22:08:14 |
 Üdv mindenkinek!
Köszönöm Kós Ritának [273] a segítséget!
57. (számozott) feladat: Egy háromszög oldalai 13, 14 és 15. Adjuk meg a pontos értékét a
a.) beírt köre sugarának
b.) TcBTa (Ta és Tc magasságtalppontok) beírt köre sugarának
c.) TcBTa háromszög területének ( a talpponti háromszög területének )
|
|
| [273] Kós Rita | 2005-07-26 19:31:42 |
 A lekepezesek szorzatarol rovidebben-hosszabban Reiman Istvan konyveiben is van szo: Fejezetek az elemi geometriabol (Typotex, pici vekony, ebben biztosan), ill. A geometria es hatarteruletei c. konyvben, ha jol emlekszem.
|
| Előzmény: [272] BohnerGéza, 2005-07-15 23:09:11 |
|
| [272] BohnerGéza | 2005-07-15 23:09:11 |
 Az 50., 51., 53. és 56. feladat közös, általános megoldása.
Igen örülök lorantfy és Kós Géza 56. feladatra a [267]-ben ill. [268]-ban leírt megoldásának. Ezek is alkalmasak az általánosításra.
Ha valaki még nem ismeri a leképezések szorzatát, annak is megérthető amit írok, de időt és energiát kell rá szánnia, végigjátszva-gondolva minden állítást!
A téma bővebb megismeréséhez Rácz János könyveit tudom ajánlani, de ezek nehezen érhetők el. Rossz memóriám miatt további könyveket most nem tudok, remélem lesz valaki és kisegít!
Jelölje az A körüli alfa forgatást (A|alfa). Legyen
(1)...(C|gamma)*(B|béta)*(A|alfa)=I helybenhagyás.
//A leképezések szorzatát - egymás utáni elvégzését - visszafelé olvasva kell értelmezni, tehát először A, majd B, végül C körül forgatunk,// Helybenhagyást akkor kapunk, ha összesen n*360 fokot, ahol n egész, forgatunk és van fixpont. Ez a fent jelzett feladatok esetén áll. Az egyszerűség kedvéért és mert ilyen esetre ezen feladatok mindig visszavazethetők n=1 (vagy -1) esettel foglalkozunk.
Tudnunk kell még, hogy egy forgatás helyettesíthető két tengelyes tükrözés szorzatával, pl. (A-alfa)=t2*t1, ahol t1 és t2 is átmegy A-n, valamint t1 és t2 szöge alfa fele az irányítást is figyelembe véve. (1)-et balról (C|-gamma)-val szorozva:
(2)...(B|béta)*(A|alfa)= (C|-gamma)
Legyen t2=AB, t1 és t3 pedig olyan egyenesek, melyekre (A|alfa)=t2*t1 és (B|béta)=t3*t2. Ekkor
(3)...(B|béta)*(A|alfa)=(t3*t2)*(t2*t1)=t3*(t2*t2)*t1=t3*t1= (C|-gamma)
Tehát t1 és t3 is átmegy C-n. Mindent végiggondolva ABC olyan háromszög kell legyen, melyben a megfelelő csúcsoknál alfa/2, béta/2 ill. gamma/2 szög van. //Feltéve, hogy egyik szög sem n*360 fok, azaz mind a három forgatás valódi fogatás. //
Jó munkát a fent jelzett feladatok átgondolásához! Kitalálható esetleg újabb konkrét feladat is?!
|
| Előzmény: [268] Kós Géza, 2005-07-11 12:00:08 |
|
| [271] Hajba Károly | 2005-07-11 16:43:28 |
 Köszi a továbbképzés. Tényleg egyszerű.
De talán már nem olyan egyszerű azon zárt görbe megszerkesztése, mely görbe bármely pontjára azonos a PA+PB+PC hossz nagysága. Ezen görbe elfajult esete az I pont is.
HK
|
| Előzmény: [270] lorantfy, 2005-07-11 15:40:54 |
|
| [270] lorantfy | 2005-07-11 15:40:54 |
 Kedves Károly!
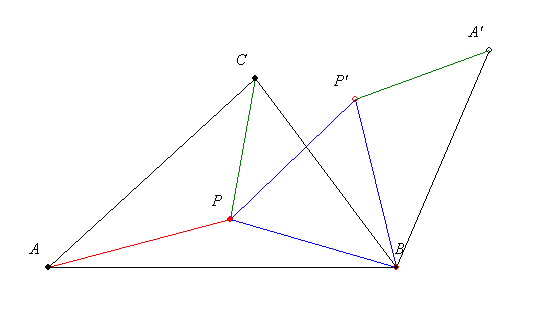
A tétel igaz: Ha az ABC hegyesszögű háromszög síkjában lévő P pontra igaz, hogy AP+BP+CP összeg minimális, akkor P a háromszög izogonális pontja (melyből mindhárom oldal 120 fokos szögben látszik.)
A bizonyítás nagyon szép és egyszerű. Forgassuk el a B pont körül a BCP háromszöget 60 fokkal. Mivel BP'P háromszög egyenlő oldalú, ezért az APP'A' törött vonal hossza megegyezik az AP+BP+CP összeggel. Az A' helyzete P-től független. APP'A' hossza akkor minimális, ha P és P' az AA' egyenesre illeszkedik. Ez pedig akkor van, ha APB és BPC és BPC 120o, vagyis ha P az izogonális pont. 120o, vagyis ha P az izogonális pont.
|
 |
| Előzmény: [269] Hajba Károly, 2005-07-11 13:31:23 |
|
| [269] Hajba Károly | 2005-07-11 13:31:23 |
 Üdv!
Érdekesnek tűnik a háromszög I pontja más szempontból is, mintha erre a pontra igaz, hogy PA + PB + PC hossz a legrövidebb, ahol A, B, C a háromszög csúcsai, míg P egy tetszőleges pont a síkjukban. Bizonyítani nem tudom, csak ráleltem. Ha igaz, gondolom egy -általam nem- ismert tétel.
Egy adtok egy kis továbbképzést vagy címeket, megköszönném. :o)
O.
|
| Előzmény: [268] Kós Géza, 2005-07-11 12:00:08 |
|
| [268] Kós Géza | 2005-07-11 12:00:08 |
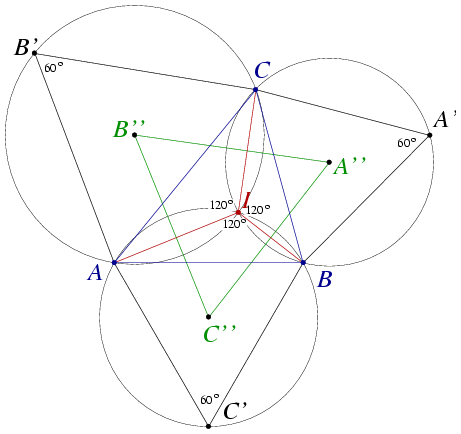
 Legyen az AC'B és BA'C köré írt körök B-től különböző metszéspontja I. Az AC'BI és BA'CI húrnégyszögek szögeiből AC'B =BA'C =BA'C =120o. Ebből következik, hogy CB'A =120o. Ebből következik, hogy CB'A =120o, vagyis az I pont a CB'A körön is rajta van. =120o, vagyis az I pont a CB'A körön is rajta van.
Ha az ABC háromszög mindegyik szöge 120 foknál kisebb, akkor I a háromszög izogonális pontja. Ha valamelyik szög éppen 120 fok vagy annál nagyobb, akkor nincs izogonális pont, és az ábra kicsit máshogy néz ki, de a három kör akkor is egy ponton megy át.
Az IA'', IB'', IC'' szakaszok (egyenesek) páronként 120 fokos (60 fokos) szöget zárnak be. Az A''B'', B''C'', C''A'' egyenesek két-két kör centrálisai, amik merőlegesen felezik az IA'', IB'', IC'' közös húrokat. Ezek az egyenesek tehát szintén páronként 60 fokos szöget zárnak be egymással.
|
 |
| Előzmény: [267] lorantfy, 2005-07-10 17:00:12 |
|
| [267] lorantfy | 2005-07-10 17:00:12 |
 Nem szeretném, ha Géza szép feladata feledésbe merülne!
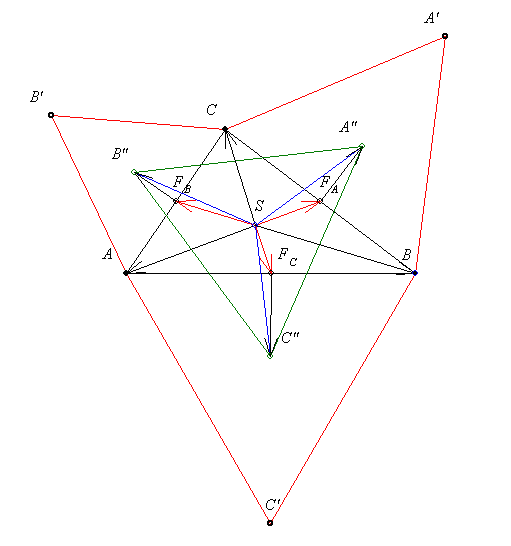
56. feladat megoldása: Helyezzük a koord.rsz. origóját a háromszög S súlypontjába.
Legyen

Fejezzük ki  vektort ezek segítségével! vektort ezek segítségével!

 pedig pedig  90 fokos, pozitív irányú elforgatottjának 90 fokos, pozitív irányú elforgatottjának  -szorosa. -szorosa.


Hasonlóan:

Az origó körüli 120 fokos, pozitív irányú forgatás mátrixa:
![\left[\matrix{cos 120^\circ &sin 120^\circ \cr -sin 120^\circ & cos 120^\circ \cr}\right]=
\left[\matrix{-\frac{1}{2}&\frac{\sqrt3}{2}\cr\frac{-\sqrt3}{2} &-\frac{1}{2} \cr}\right]](keplet.cgi?k=231A6CD88033A9CB)
Ezzel beszorozva  -t és felhasználva, hogy a,b,c vektorok összege 0, vagyis a koordinátákra is: -t és felhasználva, hogy a,b,c vektorok összege 0, vagyis a koordinátákra is:
a1+b1+c1=0, a2+b2+c2=0
 -t kapjuk. Tehát igaza van Dánielnek (=tudniakarok): valóban egyenlő oldalú háromszöget kapunk. -t kapjuk. Tehát igaza van Dánielnek (=tudniakarok): valóban egyenlő oldalú háromszöget kapunk.
|
 |
|
|
| [265] papi | 2005-07-06 08:54:13 |
 Bocsánat ! Természetesen az előbb Torricelli pontot akartam írni (papi)
|
|
| [264] papi | 2005-07-06 08:37:07 |
 Kedves Barátaim ! A h-szög nevezetes pontjainak a köré írható körre vonatkozó hatványait keresgélem. A S-pont, M-pont, beírt kör Kpontja és a Lamoine-féle pont esetében már rájöttem e hetványokra. De a Tossicelli-pontnál elakadtam. Tud valaki segíteni? (papi)
|
|
| [263] Lóczi Lajos | 2005-07-04 23:46:42 |
 Csak kiegészítésképpen írom, hogy a "négyzetes közelítés" az idézett Newton-módszerben persze nem azt jelenti, hogy a szereplő deriváltpolinom épp másodfokú, hanem azt, ahogyan a hiba nagysága csökken: a numerikus módszerek elméletéből ismert, hogy a Newton-módszer gyorsan konvergál, ha megfelelően közelről indítjuk a tényleges megoldástól (azaz z0-t "elég közel" választjuk meg a keresett értékhez, ami jelen esetben z0=1 mellett jó, de általában a pontos vonzási tartomány fraktálbonyolultságú alakzatokból áll, l. pl. http://mathworld.wolfram.com/NewtonsMethod.html)
A konvergencia a jelen esetben olyan gyors, hogy |z3-cos (10o)| 2.10-7, majd |z4-cos (10o)| 2.10-7, majd |z4-cos (10o)| 3.10-14, aztán |z5-cos (10o)| 3.10-14, aztán |z5-cos (10o)| 7.10-28, stb. 7.10-28, stb.
(A hatványsoros közelítés előnye, hogy a kezdeti értékkel nem kell bajlódni, de a konvergencia nem ennyire gyors: az n. lépésben a hiba ott n faktoriálissal arányos.)
|
| Előzmény: [261] jonas, 2005-07-02 10:28:45 |
|
|
| [261] jonas | 2005-07-02 10:28:45 |
 Az igaz, hogy a koszinusz (illetve a hatványsorba fejtése) többet mond az értékről, mint a komplex köbgyökös kifejtés.
Ennek ellenére a harmadfokú egyenlettel is lehet valamit kezdeni, ha már nadorp kiszámolta. Persze ha a megoldóképletet alkalmazzuk rá, akkor sinust kell számolni, de megoldhatjuk közvetlenül a harmadfokú egyenletet valamilyen közelítéssel. Nem nehéz négyzetes közelítést kapni:

p'(z)=12z2-3
z0=1
zn+1=zn-p(z)/p'(z)
Ekkor zn cos (10deg)=0.98481 cos (10deg)=0.98481
|
| Előzmény: [256] Lóczi Lajos, 2005-06-29 20:38:19 |
|
| [260] Lóczi Lajos | 2005-06-30 10:50:02 |
 Rosszul emlékeztem, nem "tétel"-t, hanem "vizsgakérdés"-t említett. De ez már filozófia. Attól függ, milyen kontextusban van szükség a válaszra. Numerikus matematikai szempontból a táblázat tökéletes, de elméleti szempontból nem mindig.
|
| Előzmény: [259] Lóczi Lajos, 2005-06-30 10:43:26 |
|
| [259] Lóczi Lajos | 2005-06-30 10:43:26 |
 Én is ugyanazt mondtam, mint az első 2 bekezdésed, viszont pontosan megadtam, melyik értékre kell gondolni, tehát nem értem a problémát. És ez nem a megoldóképlet baja, hanem a köbgyöké, mint jelölésé, hiszen a komplex köbgyök nem is függvény. A valós négyzetgyök  -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel. közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel.
Viszont az, hogy kikeresel valamit egy táblázatból, szerintem sosem helyes válasz egy matematikai kérdésre, mert nem konstruktív és nem mutat rá a miértre, pláne nem bizonyítás (az eredeti kérdésben "tételt" említett a hozzászóló).
|
| Előzmény: [258] Fálesz Mihály, 2005-06-30 07:03:33 |
|
| [258] Fálesz Mihály | 2005-06-30 07:03:33 |
 A megoldóképlettel az is baj, hogy például az Általad felírt alak a gyököket az 50o+k.120o és a 100o+k.240o szögfüggvényeivel fejezi ki.
Szóval nem jutottunk közelebb, de most már 9, ugyanannyira felírhatatlan szám közül kell kiválasztani a 3 gyököt, amik közül csak az egyik sin 260o, a másik kettő hamis gyök...
Szerintem a helyes válasz az lett volna, hogy (a Függvénytáblából kiolvasva)
sin 260o=sin (180o+80o)=-sin 80o -0,9848. -0,9848.
|
| Előzmény: [256] Lóczi Lajos, 2005-06-29 20:38:19 |
|
| [257] Lóczi Lajos | 2005-06-29 20:44:07 |
 Persze korrekt válasz az is, ha a szinusz-értéket kifejezed a megfelelő oldalhosszú és szögű derékszögű háromszögben a megfelelő oldalak arányával.
És még végtelen sok korrekt válasz létezik, amely sin (260o) értékét más matematikai dolgokhoz, objektumokhoz kapcsolja.
|
| Előzmény: [254] Stegi, 2005-06-28 18:50:34 |
|
| [256] Lóczi Lajos | 2005-06-29 20:38:19 |
 A harmadfokú egyenlet itt sajnos épp olyan, hogy minden gyöke valós, de a megoldóképletében a komplex számok nem kerülhetők ki. (Ez a középkor óta már sokakat idegesített :-)
A három megoldás közül a minket érdeklő most ez:

ahol i a komplex képzetes egység és a köbgyökök három lehetséges értéke közül ügyesen kell megválasztani a megfelelőt: a nevezőben szereplő komplex szám 1/3-ik hatványa az a komplex szám, melynek irányszöge 5 /18, nagysága 21/3, a számlálóban szereplő komplex szám 2/3-ik hatványa pedig az a komplex szám, melynek irányszöge 5 /18, nagysága 21/3, a számlálóban szereplő komplex szám 2/3-ik hatványa pedig az a komplex szám, melynek irányszöge 5 /9, nagysága pedig 2.21/3 -- ahol természetesen 21/3 a "közönséges" valós köbgyök. /9, nagysága pedig 2.21/3 -- ahol természetesen 21/3 a "közönséges" valós köbgyök.
Ez tehát -sin (260o) értéke. A fentiekből látszik, hogy ha ilyen formában, algebrai úton válaszolom meg a kérdést, akkor tulajdonképpen semmilyen "kezelhető", "kézzelfogható" információt nem mondtam a keresett szinusz-értékkel kapcsolatban. "A formula szép, de semmire sem jó."
Ellenben itt egy sokkal szebb és hasznosabb formula, az analízis nyelvén:

amiből tetszőleges pontossággal ki is lehet számolni a szinusz értékét.
|
| Előzmény: [255] nadorp, 2005-06-29 16:01:16 |
|
| [255] nadorp | 2005-06-29 16:01:16 |
 sin 260o=-sin 80o=-cos10o.
Ismert, hogy cos 3 =4cos3 =4cos3 -3cos -3cos  ,azaz ,azaz
cos30o=4cos310o-3cos 10o

Ez egy harmadfokú egyenlet cos10-re, ami megoldható megoldóképlettel ( ezt már nem írnám le). Szerintem a feladatra ez a korrekt válasz, de nem tudom, hogy a harmadfokú egyenlet tananyag-e ott, ahol tanulsz. Ha középiskolás vagy, akkor úgy tudom nem, ha máshová jársz, akkor attól tartok igen.
|
| Előzmény: [254] Stegi, 2005-06-28 18:50:34 |
|
| [254] Stegi | 2005-06-28 18:50:34 |
 Sziasztok!
Nagyon egyszerű, mégsem tudom. Kérek segítséget. Ez egy vizsgakérdés : "Mennyi sin 260fok?" Mi rá a korrekt válasz?
Köszönom a segítséget.
|
|
|
|
| [251] Doom | 2005-06-10 16:07:35 |
 Köszönöm mindenkinek a sok megoldást! Fálesz 2. megoldása szerintem is nagyon ötletes! :)
|
|
| [250] Fálesz Mihály | 2005-06-10 07:38:40 |
 Sziasztok,
Szerintem próbáljatok meg geometriaibb megoldásokat is kitalálni. Sok mindent ki lehet számolni, de az ilyen megoldások elrejtik a feladatok matematikai szépségeit, a kívülállónak meg azt a hamis képet mutatják, hogy csak ilyen megoldás van.
Érdemes lehet próbálkozni azzal, hogy a C csúcsból invertálunk. (Ez arra jó, hogy harmonikus közepet számtani középre cseréljük.) Utána már semmilyen számolás nem kell, csak egy ügyes segédpont, de ezt már találjátok ki Ti.
Mondanék két alternatív, kicsit számolós, de azért rövid utat is.
1. A szögfelezővektor a két oldalvektor súlyozott átlaga, a súlyokat a szögfelező-tételből megtdhatjuk. Aztán... (Valószínűleg innen jött a feladat is.)
2. Írjuk fel a CAB, CAF és CFB háromszögek területét az a,b,f szakaszokkal és a C-nél levő szögekkel.
Üdv.
F.M.
|
| Előzmény: [249] levi, 2005-06-09 22:41:50 |
|
|
|
| [247] Doom | 2005-06-09 16:21:15 |
 Bizonyítsuk be, hogy egy általános háromszög bármely 'f' szögfelezőjére igaz, hogy ha a vele szemköti oldal 'c', és a msáik kettő 'a' és 'b', akkor 'f' kisebb-egyenlő 'a' és 'b' harmonikus közepénél!
u.i.1: ha vki jól tud ábrát készíteni, nagyon megköszönném, ha csinálna hozzá egyet! :)
u.i.2: c-nem kell a feladat megértéséhez, de nem tudtam ábra nélkül máshogy elmagyarázni :(
|
|
| [246] tudniakarok | 2005-06-08 22:58:15 |
 kritsmének emailben elküldtem még tegnap este a rólad elnevezett Fálesz Mihály tételét,és megfordítását,úgyhogy már nincs rá szüksége,sőt ma a válaszlevelében megköszönte a segítséget,ugyanis 1,7-es átlaggal átment matekból! Ezúton is Grat!
|
| Előzmény: [245] Fálesz Mihály, 2005-06-08 12:35:40 |
|
| [245] Fálesz Mihály | 2005-06-08 12:35:40 |
 Egy másik topikban kritsme szerette volna megtanulni a rólam elnevezett tételt.
A Thálész-tétel azt mondja ki, hogy egy kör átmérője a kör pontjaiból derékszögben látszik (kivéve persze az átmérő két végpontját, ahol baj van az egyik iránnyal), lásd az arcképemet.
A tételnek van megfordítása és egy kicsit erősebb változata is: az átmérő a körvonal pontjaiból derékszögben, a belső pontokból tompaszögben, a külső pontokból hegyesszögben látszik. Mindennek a bizonyítása sem nehéz. Kedves Kritsme! Melyikre van szükséged?
|
|
|
| [243] BohnerGéza | 2005-06-02 18:54:34 |
 56. feladat: Az ABC háromszög oldalaira a CBA', az ACB' és a BAC' azonos körüljárású szabályos háromszöget írtuk. Ezek A", B", C" súlypontja milyen háromszöget határoz meg?
|
|
| [242] BohnerGéza | 2005-06-02 18:48:21 |
 Megjegyzések az 50. és 51. feladathoz.
Az 50. feladattal kapcsolatban Hraskó András hívta fel arra a figyelmemet, hogy tulajdonképpen Pascal-tételre feladat. Teljesen igaz, ajánlom mindenki figyelmébe! Ha valaki kedvet érez hozzá, kérem írja be bővebben ezt a megoldást!
A [239.]-ben leírt megoldásnál a Pascal-tételes általánosabb, nem használja ki, hogy F a PR felezőpontja.
Az 51. feladatot az 50. [239] vázolt megoldás közben tulajdonképpen megoldottuk (, hivatkozva az 53. feladatra). Ha valaki kedvet érez hozzá, kérem írja be ennek a megoldását!
(Még ennyi segítség mellet sem könnyű feladatok!)
|
| Előzmény: [239] BohnerGéza, 2005-05-19 19:03:44 |
|
| [241] Hraskó András | 2005-05-20 21:56:15 |
 Kedves Géza!
Az 55. feladatban kitűzött szerkesztés, azt hiszem, teljes általánosságban nem végezhető el euklideszi módszerekkel.
Ha jól látom, akkor a háromszög a, b, c oldalai és beírt körének r sugara között az
r2s-(s-a)(s-b)(s-c)=0
összefüggés áll fenn ( ). Ez c-re nézve (a-t, b-t és r-t tekintjük adottnak) harmadfokú egyenlet. A bal oldali polinom az a, b, r adatok megfelelő választása mellett a racionális számtest felett irreducibilis is, így a szerkeszthetőség elmélete (Galois elmélet) szerint c nem szerkeszthető. ). Ez c-re nézve (a-t, b-t és r-t tekintjük adottnak) harmadfokú egyenlet. A bal oldali polinom az a, b, r adatok megfelelő választása mellett a racionális számtest felett irreducibilis is, így a szerkeszthetőség elmélete (Galois elmélet) szerint c nem szerkeszthető.
|
|
|
| [239] BohnerGéza | 2005-05-19 19:03:44 |
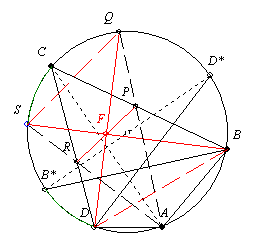
 Az 50. feladat megoldása: Sajnos a [229.] ábráján a csúcsok betűzését elrontottam, így új ábra is készült.
A megoldás vázlatát írom csak le, teret engedve az önálló munkának is.
A megoldás lényege: Legyen F a PR felezőpontja. Megmutatjuk, hogy DBF szög = DBS szöggel = béta felével. Ez elég a feladat állításának igazolásához, hiszen analóg módon igaz, hogy BDF szög = BDQ szöggel.
Az 53. feladatot felhasználva kapjuk, hogy DBF szög a béta fele.
Mivel B*BC szög a béta fele és CS ív=B*D ívvel, ezért DBS szög is a béta fele.
|
 |
| Előzmény: [227] BohnerGéza, 2005-04-14 22:32:17 |
|
|
|
|
| [235] secand | 2005-05-12 21:49:18 |
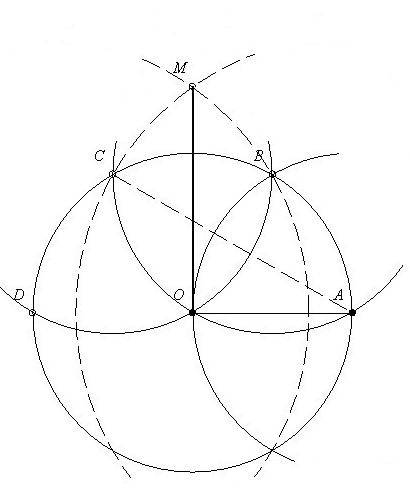
 Megoldás az 52. feladatra:
1.ábra: Az O középpontú kör egy tetszőleges pontjából(:=A) körívezzünk a megadott sugárral a kör kerületére,így kapjuk a B,C,D pontokat!Az AC szakasz a körbe írható szabályos háromszög oldala,ezt körzőnyílásba véve,és körözve A illetve D pontokból metszéspontként kapjuk M pontot!Pit. tétellel belátható hogy az OM szakasz a körbe írható négyzet oldala,így már könnyen oszthaó a kör négy egyenlő ívre,ahonnan már csak néhány,a megadott sugárral való körzés választ el a négy területrésztől...
|
 |
| Előzmény: [228] tudniakarok, 2005-04-20 22:03:19 |
|
| [234] KiCsa | 2005-05-12 15:04:27 |
 55. feleadat: Szerkesszünk háromszöget, ha adott két oldala és a beírt kör sugara!
Bocsánat ha lett volna.
|
|
| [233] joe | 2005-05-10 18:44:56 |
 54. feladat: Legyen k egy félkör O középponttal és AB átmérővel. Legyen M a BA félegyenessel ellentétes félegyenes egy B-től különböző pontja. Az AB-től különböző p egyenes haladjon keresztül az M ponton és messe a k félkört két, egymástól különböző C és D pontban, miközben |MC| > |MD|. Legyen K az AOC és a BOD háromszögek köré írt köreinek O-tól különböző metszéspontja. Bizonyítsuk be, hogy OK merőleges MK-ra.
|
|
| [232] BohnerGergő | 2005-05-05 19:28:02 |
 Kiegészítés az 53. feladat megoldásához:
Az indoklásból kimaradt, hogy a két forgatás szorzata azért egyenlő az F körüli 180 fokos forgatással, mert a két forgatás szögének összege 180 fok.
|
| Előzmény: [231] BohnerGergő, 2005-05-05 19:03:13 |
|
| [231] BohnerGergő | 2005-05-05 19:03:13 |
 D-nél a szög delta, E-nél epszilon. Tudjuk: epszilon=180-delta Az egyenlőszárú háromszögek miatt, ha A-t forgatjuk E körül epszilonnal, majd D körül deltával akkor B-t kapjuk. Ugyanígy A-ból B-t kapjuk ha középpontosan tükrözzük F-re. Egy forgatás két tengelyes tükrözés szorzata, még pedig akkor, ha a tengelyek szöge fele a forgatás szögének. Vegyük fel a 3 tükörtengelyt az ábrán látható módon. Ekkor: DEF szög 90-(delta/2) és EDF szög delta/2. Ekkor DFE szög 180-(90-(delta/2)+delta/2)=90
|
 |
| Előzmény: [230] BohnerGéza, 2005-04-28 21:55:56 |
|
| [230] BohnerGéza | 2005-04-28 21:55:56 |
 53. feladat: (egyben segitség az 50,-hez) Az ABC háromszög BC és CA oldalaira, mint alapra, kifelé ( vagy mindkettőt befelé) rakjuk a BDC ill. a CEA egyenlő szárú háromszögeket. A D-nél delta, az E-nél 180 fok mínusz delta szög legyen. Jelöljük AB felezőpontját F-fel. Bizonyítandó, hogy a DEF háromszögben F-nél derékszög, D-nél delta/2 szög van!
(Használjuk fel, hogy a forgatás helyettesíthető két tengelyes tükrözéssel!)
|
|
|
| [228] tudniakarok | 2005-04-20 22:03:19 |
 Nem tudom,hogy volt-e már,de ez egy igen érdekes, tanulságos és egyszerű? feladat:(Napóleon egyik feladata)
52.feladat: Osszunk fel egy r sugarú kört négy egyenlő területrészre! KIZÁRÓLAG KÖRZŐT használhatunk!
|
|
| [227] BohnerGéza | 2005-04-14 22:32:17 |
 Az előző hozzászólás feladata legyen az 50. feladat! Talán némi segítség a megoldásához:
51. feladat: Legyen az 50. feladatban F a PR felezőpontja. Igazoljuk, hogy a QSF háromszögben F-nél derékszög van és Q-nál a B-nél lévő szög fele.
|
| Előzmény: [226] BohnerGéza, 2005-04-12 12:35:53 |
|
| [226] BohnerGéza | 2005-04-12 12:35:53 |
 Az ABCD húrnégyszögben (AB<BC és AD<DC) az A-ból a B belső szögfelezőjére állított merőleges messe BC-t P-ben, a körülírt kört Q-ban, hasonlóan a D belső szögfelezőjére állított merőleges DC-t R-ben, a kört S-ben. Igazolandó, hogy a BS, a DQ és a PR egyenesek egy pontban metszik egymást.
|
|
|
| [224] Hajba Károly | 2005-03-22 09:30:17 |
 Üdv a Geométereknek!
Két érdekes Penrose féle csempe kerestetik. Ha valaki ismeri, szóljon! Közölje itt a paramétereit! :o)
Az alábbi idézet ebből a cikkből való.
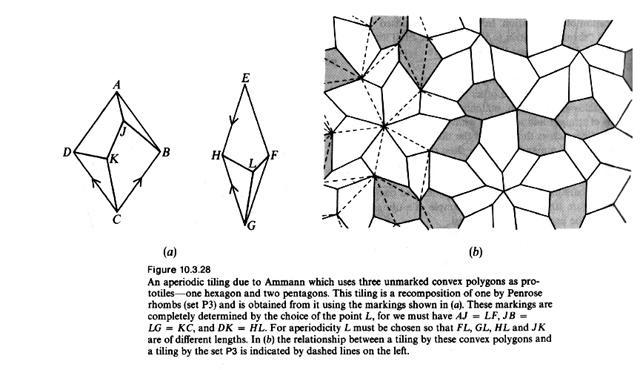
"Bármelyik, sárkányokról és dárdákról szóló tétel átalakítható a Penrose-rombuszokról szóló tétellé, vagy akármelyik Penrose-féle csempepárról szólóvá, és viszont. Conway a sárkányokkal és dárdákkal dolgozik szívesebben, más matematikusok jobban szeretik az egyszerűbb rombuszokat. Robert Ammann elképesztően sokféle nem periodikus csempekészletet talált ki. Az egyik készlete, amely két konvex ötszögből és egy konvex hatszögből áll, az élek bármilyen eltorzítása vagy színezése nélkül kényszeríti ki a nem periodikus csempézést. Több olyan hatszögekből álló párt talált, ahol a hatszögek öt belső szöge 90 fokos, egy pedig 270 fokos. E készletek leírása és figyelemre méltó tulajdonságaik tárgyalása megtalálható Branko Grünbaum és G. C. Shephard "Some Problems on Plane Tilings" című könyvében."
Az alábbi kép az idézett könyvből való, de ez nem az 1. keresett csempekészlet.
Ha valaki tud segíteni, azt előre is megköszönöm.
HK
|
 |
|
| [223] Hraskó András | 2005-03-22 06:04:11 |
 Csak úgy a poén kedvéért egy újabb megközelítés a Géza 206. problémájához és a 210-es általánosításhoz.
Tekintsük a k kört a hiperbolikus geometria Cayley Klein modellje alapkörének (lásd Kós Géza írását: itt.)
Ha tekintünk egy A pontot a körön belül, és a kör pontjait átvetítjük A-n át a körre, akkor igazából a hiperbolikus geometriában az A-ra vonatkozó középpontos tükrözés hatását tekintjük a sík végtelen távoli pontjain.
Ha A a körön kívül van, akkor a transzformáció az A polárisának megfelelő hiperbolikus egyenesre vonatkozó tengelyes tükrözés.
Ha A, B, C egy egyenesen vannak (és mind kívül), akkor a három tengelyes tükrözés három egy ponton átmenő egyenesre történik. Ez a pont az ABC egyenes pólusa.
Innen a megoldás a 208. hozzászólásban leírttal analóg.
Persze, ha A, B, C közt van belső pont is, akkor kissé más a helyzet, de ezt meghagyom gondolkoznivalónak.
|
|
| [222] lorantfy | 2005-03-21 10:09:41 |
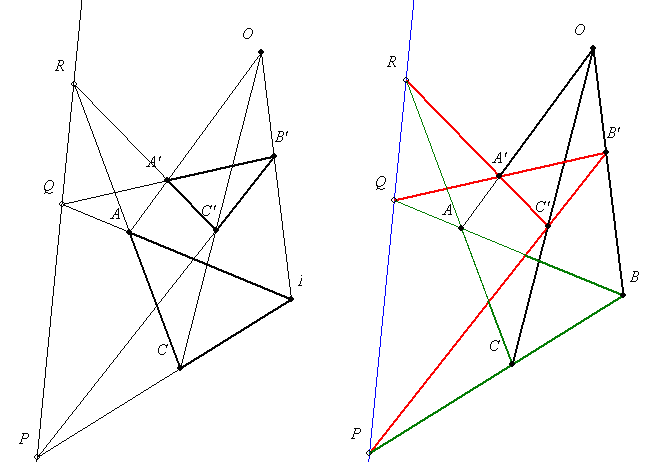
 Kedves András!
Köszönöm a hozzásolásodat! A térbeli ábra azért született, mert Desargues perspektív háromszögekre vonatkozó tételére gondoltam, ahol a két háromszöget két metsző síkra helyezve, gyakorlatilag nincs mit bizonyítani, hiszen a megfelelő metszéspontok, csak a két sík közös egyenesén lehetnek.(Pirossal és zölddel szineztem a két síkban futó egyeneseket.) Tehát síkban valami elveszik ami térben még nyilvánvaló.
|
 |
| Előzmény: [221] Hraskó András, 2005-03-21 05:25:19 |
|
| [221] Hraskó András | 2005-03-21 05:25:19 |
 Kedves László!
Nem egészen értem, hogy és miért készíted a térbeli ábrádat, de fontos dolgot kapisgálsz az biztos.
Ha jól látom, Pascal tételének volt egy lényeges szerepe a matematika történetében és ez nagyon hasonlatos az itt történt eseményekhez.
Pascal saját tételét egy oldalon hirdetésként tette közzé, bizonyítás nincs is rajta, csak Desargues tevékenységére való utalás van és az a megjegyzés, hogy a kúpszeletet átvetítheti körbe, így elég körre bizonyítani.
Poncelet a XIX. században újra elővette a problémát. Így kezdi: a Pascal tétel körre egyszerűen igazolható, ha két metszéspont (pld P1P2 P4P5 és P2P3 P4P5 és P2P3 P5P6) az ideális egyenesen van. Ez lényegében Géza eredeti (206. hozzászólás) feladata. P5P6) az ideális egyenesen van. Ez lényegében Géza eredeti (206. hozzászólás) feladata.
Ezután Poncelet arra hivatkozik, hogy bármely kör és egyenes átvetíthető a tér egy pontjából egy másik síkra, úgy, hogy a körből kör legyen, az egyenes pedig az ideális egyenesre képződjék.
Ez szép feladat abban az esetben, ha az eredeti kör és egyenes nem metszi egymást (érdemes elolvani hozzá - és kijavítani - Sain Márton: Nincs királyi út című könyvében az Apollóniuszról szóló részt).
Ellentmonádosnak látszik abban az esetben, ha a kör és az egyenes metszi egymást. Azt hiszem az "egyszerű" bizonyításnak ez a gátja is inspirálhatta Poncelet-t, hogy megalkossa a komplex projektív teret és a körök közös ideális pontjának fogalmát.
|
|
| [220] lorantfy | 2005-03-19 23:07:34 |
 Kedves András!
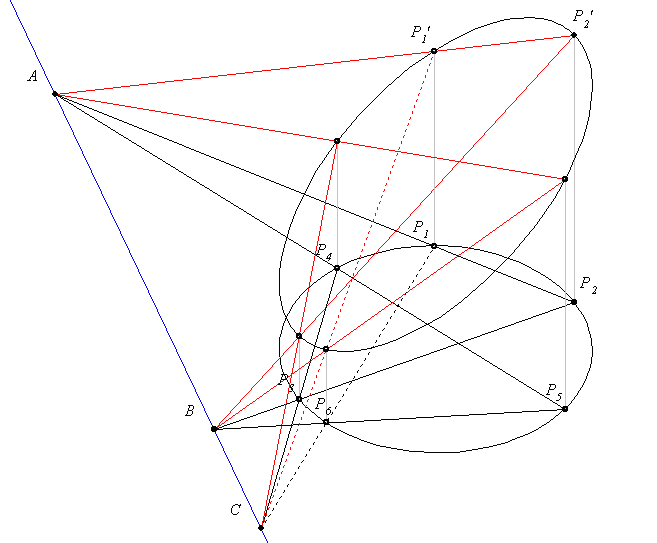
Gratulálok! Nagyon szép gondolat. Valami hasonlóra gondoltam, csak persze sokkal primitívebb módon:
Az A,B,C pontokra vonatkozó középpontos hasonlóságokat kétszer "oda-vissza" alkalmazva a pontokban állított - ábra szerint keletkező - síkra merőleges szakaszokra végül a P7P7'=P1P1' egyenlőséghez jutnánk, ami már elegendő lenne a bizonyításhoz. Sajnos  nem teljesül. Az ábra kicsit bonyodalmasnak tűnik, de érdemes megvízsgálni. Két síkról van szó, melyek metszésvonala AC egyenes. nem teljesül. Az ábra kicsit bonyodalmasnak tűnik, de érdemes megvízsgálni. Két síkról van szó, melyek metszésvonala AC egyenes.
|
 |
| Előzmény: [219] Hraskó András, 2005-03-16 23:29:08 |
|
| [219] Hraskó András | 2005-03-16 23:29:08 |
 Kedves Szefoharcos!
Köszönöm a szép megoldást.
Egy további általánosítás is igaz. A kört (másodrendű görbét) és az A, B, C pontok egyenesét összevonhatjuk egyetlen harmadrendű görbévé.
Az E harmadrendű görbe egy O pontja meghatározza a görbe önmagára való leképezését a következő módon. Ha P E akkor legyen P' az a pont, amelyre O, P és P' valamely egyenesnek a harmadrendű görbével való (multiplicitással számítva) három metszéspontja. Nevezzük ezt a transzformációt az E görbe O centrumú tükrözésének.(Vigyázat O nem feltétlenül fixpontja e leképezésnek, hiszen O képe a görbe O-beli érintőjének E-vel való további metszépontja!) E akkor legyen P' az a pont, amelyre O, P és P' valamely egyenesnek a harmadrendű görbével való (multiplicitással számítva) három metszéspontja. Nevezzük ezt a transzformációt az E görbe O centrumú tükrözésének.(Vigyázat O nem feltétlenül fixpontja e leképezésnek, hiszen O képe a görbe O-beli érintőjének E-vel való további metszépontja!)
Állítás: az E-tükrözések olyanok mint a sík középpontos tükrözései, azaz:
0. E-tükrözés négyzete identikus.
1. Három E-tükrözés kompozíciója is E-tükrözés. (Ebből következik az eredeti tétel, hiszen abban az A, B, C, A, B, C centrumú E-tükrözések kompozíciójáról van szó és az első három kompozíciója megegyezik az utolsó hároméval, így 0. szerint kész is vagyunk.
2. A két E-tükrözés kompozíciójából származó transzformációk olyanok, mint a sík eltolásai, azaz csoportot alkotnak, és az identitáson kívül egyiknek sincs fixpontja.
Géza feladta a labdát, ez véletlenül épp a doktorim témája, lásd
http://matek.fazekas.hu/portal/tanitasianyagok/Hrasko_Andras/doktori/index.html
|
|
| [218] BohnerGéza | 2005-03-16 17:48:13 |
 Szefoharcos megoldása rögtön egy teljesebb általánosítást is elbírt volna, azaz a kör helyett tetszőleges másodrendű görbéből ( egyenespárból is ) kiindulhatunk. Játéknak sem rossz ilyeneket egy szerkesztőprogrammal ( pl, Euklides-szel ) rajzolgatni.
|
| Előzmény: [216] szefoharcos, 2005-03-16 00:54:05 |
|
|
| [216] szefoharcos | 2005-03-16 00:54:05 |
 Sziasztok!
Érdekes megfogalmazása ez a feladat a Pascal-tételnek. Ha ugyanis egy kicsit belegondolunk, látszik, hogy erről van szó. Vegyük azt az álapotot, amikor eljutunk a P6 ponthoz! Ekkor van egy húrhatszögünk; persze a pontokat index szerinti sorrendben kell tekinteni. A megfelelő "szemközti oldalpárok" metszéspontja közül A és B már adott. A Pascal-tétel miatt a harmadik metszéspont rajta van AB egyenesén, és persze P3P4-en, így az csak C lehet. Tehát P6,P1 és C kollineáris; ezt fogalmazta meg a kitűző úgy, hogy CP6 egyenese a kört P1-ben metszi. A Papposz-Pascal-tétel ellipszisre is igaz, ezzel a feladat általánosítása is rögtön adódik.
|
|
|
| [214] lorantfy | 2005-03-14 22:12:22 |
 Hello Attila!
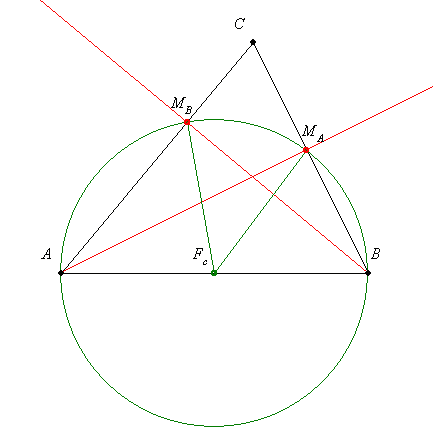
Ezek a feladatok nagyon egyszerűek, de én azért el tudom képzelni, hogy van akinek ezek is problémát okoznak. Az első lépéseket is meg kell tenni és ezek a legnehezebbek, csak vannak akik erre már nem emlékeznek.
A magasságok merőlegesek az oldalakra, így a magasságok talppontjaiban derékszögek vannak. Ha AB felezőpontjából rajzolsz egy kört AFc sugárral, akkor a Thálesz tétel szerint ezen a körön rajta lesz mindkét magasság talppontja. Tehát egyenlő (sugár) távolságra vannak az oldal felezőpontjától.
A háromszög területét ki tudod számítani az oldal és a hozzá tartozó magasság szorzataként. Tehát az oldalak és a magasságok között fordított arányosság van, hiszen szorzatuk állandó. Ekkor viszon az oldalak és a magasságok reciprokai között egyenes arányosság van, mivel ezeket használva a terület képletekben a hányadosok lesznek állandók, ugyanis a magassággal való szorzás helyett oszthatunk a reciprokával.
Ha két szög összege 180 fok, akkor a feleik összege 90 fok.
|
 |
| Előzmény: [213] Attila89, 2005-03-14 18:52:48 |
|
| [213] Attila89 | 2005-03-14 18:52:48 |
 Hello mindenkinek!Kaptam 3 feladatot,melyek hát kicsit kifogtak rajtam.Nagyon hálás lennék,ha valaki,még ha csak az egyikben is tudna segíteni.Előre is köszönöm.Az első: Bizonyítsuk be,hogy egy háromszög magasságának talppontjai egyenlő távolságra vannak a harmadik oldal felezőpontjától. A második: Igazoljuk,hogy a háromszög oldalai és a hozzájuk tartotó magasságok reciprokai között egyenes arányosság van. A harmadik: Bizonyítsuk be,hogy a háromszög bármelyik csúcsából induló belső és külső szögfelező merőleges egymásra. És tényleg köszönöm a segítséget.
|
|
|
|
| [210] Hraskó András | 2005-03-01 23:40:11 |
 Általánosítsuk Géza 206-os felszólalásban kitűzött példáját. Az általánosításnak két fokozatát látom, egyelőre csak az elsőt mondom el, hátha rájön valaki a további általánosításra.
Legyen adott a k kör és az A, B, C kollineáris pontok a síkon. Tekintsük a k kör tetszőleges P1 pontját, és k további Pk pontjait úgy, hogy P1P2 átmenjen A-n, P2P3 a B-n, P3P4 a C-n, P4P5 megint A-n, P5P6 a B-n, végül P6P7-t a C-n. Igazoljuk, hogy P7=P1.
|
|
|
| [208] BohnerGéza | 2005-02-28 22:24:20 |
 A [206]-ban szereplő feladat egy megoldása Hraskó Andrástól:
Az adott iránnyal párhuzamos húzás helyett alkalmazzunk tengelyes tükrözést, az irányra merőleges, a kör kp-ján átmenő egyenesre. Csak azt kell igazolni, hogy a t1 t2 t3 t1 t2 t3 kompozíció az identitás, ami nem nehéz.
/ Az első három és a második tükrözés szorzata is ugyanarra az egy tengelyre tükrözéssel helyettesíthető. /
|
| Előzmény: [206] BohnerGéza, 2005-02-21 23:55:14 |
|
| [207] lorantfy | 2005-02-27 16:19:32 |
 Kedves Géza!
Jó a feladat! Egyetlen gondom van vele, hogy nem én találtam ki :-)
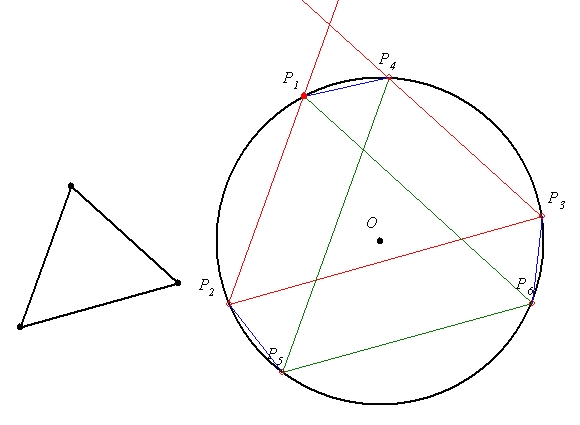
49. feladat megoldása: P4P5 párhuzamos P1P2, így P1P2P5P4 húrtrapéz, vagyis szárai egyenlőek. Hasonlóan húrtrapézok lesznek a P2P3P6P5 és P3P4P7P6 négyszögek. Száraik mind egyenlőek, tehát
P1P4=P7P4, vagyis P1=P7.
|
 |
| Előzmény: [206] BohnerGéza, 2005-02-21 23:55:14 |
|
| [206] BohnerGéza | 2005-02-21 23:55:14 |
 Adott három tetszőleges irány (egyenes ) és egy kör. Vegyünk föl a körön egy P1 pontot,a további P-k is a körön legyenek úgy, hogy P1 P2 párhuzamos az első iránnyal, P2 P3 a másodikkal, P3 P4 a harmadikkal, P4 P5 az elsővel, ... . Igazoljuk, hogy P1=P7!
|
|
| [205] BohnerGéza | 2005-02-18 15:02:17 |
 A síkbeli egybevágősági leképezések számítógépes megvalósítása legegyszerűen mátrixok segítségével oldható meg.
A forgatás mátrixa a következő, ahol alfa a forgatás szöge a (p,q) pont az origó képe, ez külön, egyszerűen számolható.
|
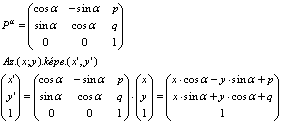 |
| Előzmény: [200] lorantfy, 2005-01-30 21:58:51 |
|
| [204] petrot | 2005-02-01 14:59:46 |
 Kedves fórumozók!
Fel szeretném hívni a figyelmeteket egy 3D szerkesztőprogramra, remélem tetszeni fog!
link: http://euler3d.uw.hu
Várom a véleményeteket (+,-), hozzászólásotokat!
Üdv! petrot
|
|
| [203] lorantfy | 2005-01-31 22:24:35 |
 Kedves 2501!
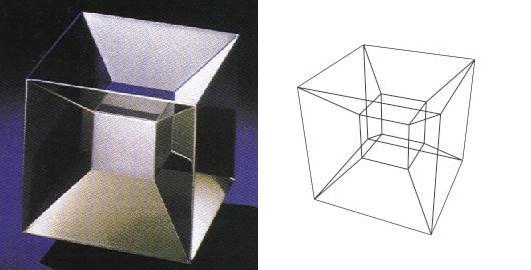
Kösz a segítséget és jó a példa is ami a témában a 48. feladat. Én még adós vagyok a 4D-s kocka 3D-s vetületével. A kockavázra feszülő szappanhártya-minimálfelületre hasonlít.
|
 |
| Előzmény: [202] 2501, 2005-01-31 10:54:54 |
|
|
|
| [200] lorantfy | 2005-01-30 21:58:51 |
 Kedves Fórumosok!
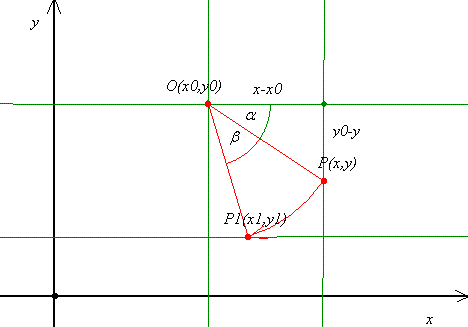
"Zoleka"-tól kaptam a feladatot e-mail-ben. Programot ír és kellene Neki P pont elforgatása  szöggel adott O pont körül. szöggel adott O pont körül.
1. Kiszámolni  szöget: szöget: 
2. 
3. Az új koordináták:
x1=x0+rcos( + + ) )
y1=y0-rcos( + + ) )
Ha tudtok jobbat írjátok be, vagy bármi más geometriát, mert elhal a téma!
|
 |
|
| [198] lorantfy | 2004-11-28 17:10:22 |
 Kedves Károly!
Te mindig egy lépéssel előttem jársz. Gondoltam felteszi valaki az ábrát, aztán megbeszéljük hogyan öröklődnek felfelé a tulajdonságok. Te ezt már megtetted, köszönet!
|
| Előzmény: [197] Hajba Károly, 2004-11-28 00:29:26 |
|
| [197] Hajba Károly | 2004-11-28 00:29:26 |
 47. feladathoz:
Vizsgáljuk meg, hogy egy adott dimenziónál hogyan alakítjuk ki a dimenzónagyságra jellemző egységnyi idomot. Mivel olyan magasabb dimenziójú idomról is beszélnünk kell, mire nincs szavunk, az alábbi egységes jelölésrendszert vezetem be. D - dimenzió mértéke, ID,d a D dimenzióbeli egységidom d dimenziójú egységidomelemének számossága. Értelemszerűen D d d 0. Így a pont jelőlése ID,0, egységszakasz ID,1, egységnégyzet ID,2, egységkocka ID,3, míg a keresett 4. dimenziójú egységidom ID,4. 0. Így a pont jelőlése ID,0, egységszakasz ID,1, egységnégyzet ID,2, egységkocka ID,3, míg a keresett 4. dimenziójú egységidom ID,4.
Az egységpont I0,0=1, egységszakasz I1,0=2, I1,1=1, azaz a kisebb dimenziójú egységidomot egységnyivel eltolom az új dimenzióiránnyal párhuzamosan. I0,0=1 megduplázódik I1,0=2 és bejön I1,1=1. Az egységnégyzet I2,0=4, I2,1=4, I2,2=1, itt már pontosan leírhatjuk az adott elem dimenzónövekedéssel járó elemszám növekedését. Azaz az eltolás miatt megduplázzuk és hozzájön az eggyel kisebb dimenziójú elemek száma, melyből az eltolással aktuális dimenziójú elem keletkezett. ID,d=2*ID-1,d+ID-1,d-1
Tehát a 4 dimenziójú egységidom részegységidomai a következők. Pont: I4,1=16, egységszakasz: I4,2=32, egységnégyzet: I4,2=24, egységkocka: I4,3=8, 4 dimenziós egységidom: I4,4=1. A 4 dimenziójú kocka síkbeli ábrája egy olyan gráf, melynek 16 pontja van, minden pontból 4 él indul ki, mely összesen 32 él és bármely pontból kiindulva 4+2n(n 0,N+) lépésszámmal lehet visszaérni. Továbbá a négyes hurkok négyzet vagy trapéz alakot adnak ki. 0,N+) lépésszámmal lehet visszaérni. Továbbá a négyes hurkok négyzet vagy trapéz alakot adnak ki.
HK
|
| Előzmény: [196] lorantfy, 2004-11-27 23:06:38 |
|
| [196] lorantfy | 2004-11-27 23:06:38 |
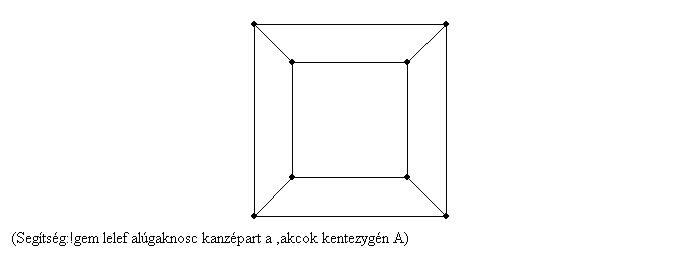
 47. feladat: Jelenítsük meg a láthatatlant! (lásd könyvajánló) Az ábrán egy 3 dimenziós kocka 2 dimenziós képe látható. Lépjünk egy dimenzióval feljebb!
Rajzoljuk meg egy 4 dimenziós "kocka" 3 dimenziós vetületének síkbeli ábráját!
Hány 3 dimenziós kocka határolja a 4 dimenziós testet?
|
 |
|
|
|
|
| [192] BohnerGéza | 2004-11-25 18:38:10 |
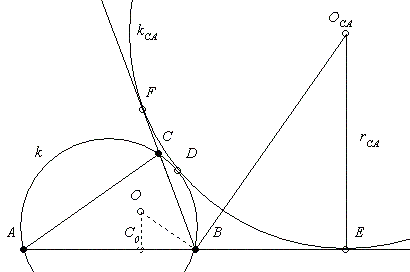
 A 45. feladat [182.] egy megoldása. A Fórum - Kürschák-verseny 5. hozzászólásában szerepel a Casey-tétel. Az alapkör a k körülírt kör, az érintőkörök: az A, B és C nullkörök, valamint a k-ca kör. Jelöljük a BF=BE szakaszt x-szel, ekkor AB*CF+BF*CA=AE*BC, azaz c(x-a)+xb=(c+x)a. Innen (b+c-a)x=2ca, 2(s-a)x=2ca, ( innen olvashatóbban a következő hozzászólásban! ) x=ca/(s-a). Tekintve, hogy a BEOca és az OCoB háromszögek hasonlók ( O a beírt kör sugara, így OCo=ró és CoB=s-b ) r-ca=ca(s-b)/ró(s-a).
A folytatás a jobb olvashatóság érdekében ( és lustaságom miatt ) a következő hozzászólásban lesz.
Megjegyzések:
1.A feladatot elkapkodva adtam föl, így szövegéből kimaradt, hogy a körülírt kört kívülről érintő körről van szó, valamint a három megadott sugár szorzata nem adható meg csak a körülírt kör sugara és a félkerület szorzatával.
2.A k-ac kör és a k-ca két különböző kör, ilyen jellegű - a körülírt kört kívülről érintő - kör 6 db van.
|
 |
| Előzmény: [182] BohnerGéza, 2004-11-17 09:35:09 |
|
|
| [190] Hajba Károly | 2004-11-24 14:47:40 |
 Kedves Svejk!
Félrevezető a vastag keret. Átrajzoltam vékonnyal és behúztam az igazi átfogót.
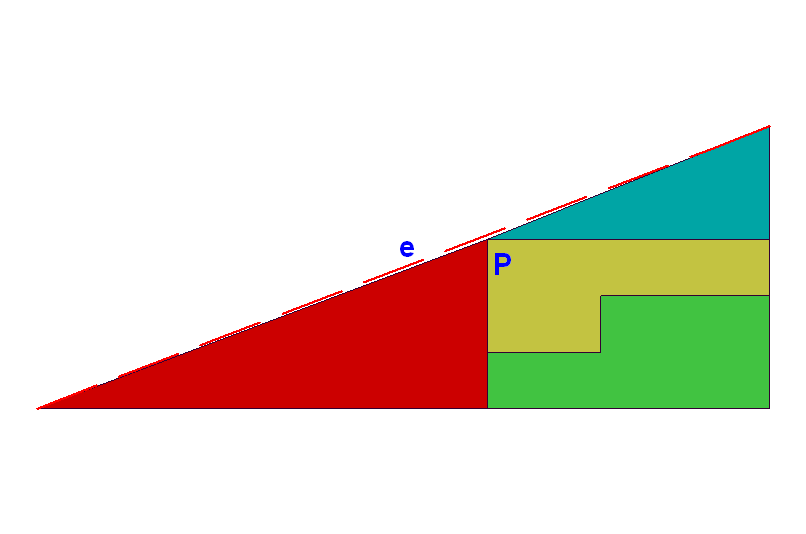
Cserébe mondd meg nekünk, hogy mennyi a P töréspont és e átfogó közötti távolság, ha a háromszög két befogója 13 és 5 egység.
HK
|
 |
| Előzmény: [187] svejk, 2004-11-24 13:22:42 |
|
|
| [188] jenei.attila | 2004-11-24 13:23:21 |
 Az a baj, hogy a befoglaló "háromszög" nem háromszög, csak majdnem. Ugyanis ha az lenne, akkor a piros és a sötétzöld háromszögeknek hasonlóaknak kellene lenni, de nem azok (2/5 nem = 5/8).
|
| Előzmény: [186] svejk, 2004-11-24 13:15:02 |
|
| [187] svejk | 2004-11-24 13:22:42 |
 Kedves Matekosok!
Elnézést, hogy előbb a képet küldtem.:( Úgy tudom, hogy ez egy elég régi feladvány, de még senkitől nem kaptam kielégítő magyarázatot, hogy miért változnak meg a részterületek összegei. Help!
A választ előre is köszönöm!
|
|
|
| [185] Kós Géza | 2004-11-22 16:34:40 |
 Kedves Géza,
Ezek szerint a kívülről érintő körökre gondoltál.
Invertáljuk a beírt kört és a BC egyenest az A középpontú,  sugarú körre, majd mindkettőt tükrözzük az A-ból induló szögfelelezőre. A B és C pont képe önmaga, a BC egyenes képe a körülírt kör, a beírt kör képe pedig az AB és AC félegyeneseket, valamint a körülírt kört érintő kör, vagyis kbc. sugarú körre, majd mindkettőt tükrözzük az A-ból induló szögfelelezőre. A B és C pont képe önmaga, a BC egyenes képe a körülírt kör, a beírt kör képe pedig az AB és AC félegyeneseket, valamint a körülírt kört érintő kör, vagyis kbc.
A beírt körnek az AB, AC félegyeneseken levő érintési pontjai az A ponttól s-a távolságra vannak. A kbc kör érintési pontjai ennek megfelelően  távolságra vannak A-tól. A sugarak aránya ugyanaz, mint az érintő szakaszoké, tehát távolságra vannak A-tól. A sugarak aránya ugyanaz, mint az érintő szakaszoké, tehát

Mindhárom körre felírva és összeszorozva,

Beírva a Héron-képletet és a  területképleteket, területképleteket,

|
| Előzmény: [184] BohnerGéza, 2004-11-19 14:22:11 |
|
|
| [183] Kós Géza | 2004-11-17 18:12:11 |
 Nekem az jött ki, hogy ha a három kör kívülről érinti a körülírt kört, akkor

és a szorzatot nem lehet csak r-rel és s-sel kifejezni, de ki lehet fejezni a beírt és körülírt kör sugarával.
Ha a három kör belülről érinti a körülírt kört, akkor

|
| Előzmény: [182] BohnerGéza, 2004-11-17 09:35:09 |
|
| [182] BohnerGéza | 2004-11-17 09:35:09 |
 45. feladat: A r-ca jelentse az ABC háromszög körülírt körét, valamint az AB és BC - ilyen irányú - félegyeneseket érintő kör sugarát. Mennyi az r-ca, r-ab és r-bc szorzata a körülírt kör r sugarával és az s félkerülettel kifejezve?
|
|
|
| [180] lorantfy | 2004-11-10 20:31:38 |
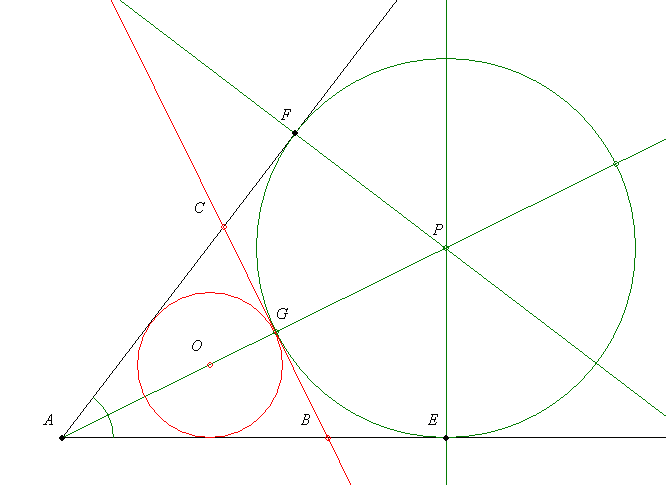
 44. feladat megoldása: Vegyük fel az  szöget és mérjük fel a száraira a félkerületet. A kapott E és F pontban állítsunk merőlegest. Ezek metszéspontja P a háromszög kívülírt körének középpontja, sugara ra=PE. Rajzoljuk meg a kört! Az a oldal ennek a körnek érintője. Húzzuk meg az AP szögfelezőt, ez a kört a G pontban metszi. szöget és mérjük fel a száraira a félkerületet. A kapott E és F pontban állítsunk merőlegest. Ezek metszéspontja P a háromszög kívülírt körének középpontja, sugara ra=PE. Rajzoljuk meg a kört! Az a oldal ennek a körnek érintője. Húzzuk meg az AP szögfelezőt, ez a kört a G pontban metszi.
A háromszög területe T= s. Mivel s adott, ez akkor a legnagyobb, ha a beírt kör a lehető legnagyobb. Ez pedig akkor van ha a beírt kör G pontban érinti a kívülírt kört. s. Mivel s adott, ez akkor a legnagyobb, ha a beírt kör a lehető legnagyobb. Ez pedig akkor van ha a beírt kör G pontban érinti a kívülírt kört.
Tehát a maximális területű háromszög egyenlő szárú.
Így a szerkesztés befejezése egyszerű: Állítsunk merőlegest a G pontban a szögfelezőre, ez lesz az a oldal.
|
 |
| Előzmény: [177] BohnerGéza, 2004-11-09 10:36:42 |
|
|
| [178] BohnerGéza | 2004-11-09 13:29:57 |
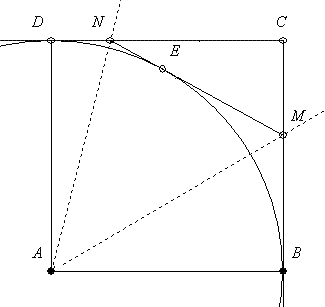
 A B.3736. feladat és egy megoldása: Az egységnyi oldalú ABCD négyzet CD oldalán adott az N, CB oldalán pedig az M pont úgy, hogy az MCN háromszög kerülete 2. Mekkora az MAN szög?
Adott az MCN háromszög egy szöge (derékszög) és kerülete, ami kettő. Így félkerülete s=1. Tudjuk, hogy a csúcsból a szemközti hozzáírt körig húzott érintőszakasz hossza s, így esetünkben a C-vel szemközti érintőkör B-nél ill. D-nél érinti a C-ből induló oldalakat, tehát középpontja A. Az AM és AN az MCN külső szögfelezői. Tükrözve AM-re B-t a E-t, majd AN-re E-t a D-t kapjuk. A két tengelyes tükrözés B-t A körül 90 fokkal forgatta el, így a két tengely szöge 45 fok.
|
 |
|
| [177] BohnerGéza | 2004-11-09 10:36:42 |
 44. feladat: . Szerkesztendő a lehető legnagyobb területű háromszög, ha adott egy szöge és a kerülete!
|
|
| [176] matekos04 | 2004-11-08 19:54:26 |
 Udv. mindenkinek!
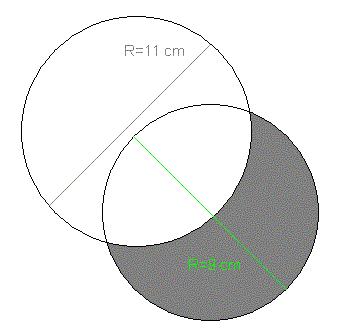
Maglattam ezt a topikot erdekesnek talaltam es gondoltam hogy bekuldök egy feladatot:
A kerdesem az hogy hany negyzetcentimeter a szurke terulet.
|
 |
|
|
| [174] lorantfy | 2004-10-24 11:21:22 |
 Kedves Géza!
A 42. feladatra egy látványosabb bizonyítást szerettem volna adni, de idő hiányában beérem azzal, hogy visszavezetem egy ismert összefüggésre. Hivatkozok - és egyben felhívom a figyelmeteket - Kiss György: Amit jó tudni a háromszögekről című cikkére itt.
42. feladat megoldása:
Bizonyítandó: 
Felhasználjuk, hogy 
Tehát, be kell látnunk, hogy  Átszorozva: Átszorozva: 
|
| Előzmény: [172] BohnerGéza, 2004-10-21 09:01:05 |
|
|
| [172] BohnerGéza | 2004-10-21 09:01:05 |
 41. feladat: Az ABC háromszög szokásos jelölései mellett (O a beírt, Oa az A-val szemközti hozzáírt kör középpontja) igazoljuk, hogy AO*AOa = b*c.
42. feladat: ( ró a beírt kör, r a körülírt kör sugara ) bizonyítandó, hogy
ró = 4r*sin(alfa/2)*sin(béta/2)*sin(gamma/2)
|
|
|
| [170] BohnerGéza | 2004-10-14 22:50:38 |
 40. feladat: Az ABC háromszög és a k-val jelölt kör feleljen meg a 37. feladatban ( [169.] hozzászólásban ) leírtaknak. Igazoljuk, hogy ABC magasságpontja k-n van! ( pontosítható az állítás )
Ez a feladat ötletet adhat a 37. feladat megoldásához, illetve segíthet a [169.] hozzászólásban vázolt számolásban.
|
| Előzmény: [158] BohnerGéza, 2004-09-08 20:25:06 |
|
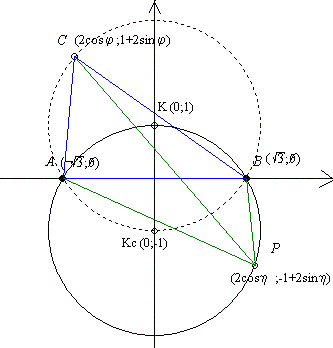
| [169] BohnerGéza | 2004-10-11 15:47:59 |
 A 37. feladat: megoldásához. Egyelőre nincs jobb ötletem, mint a koordináta geometriai út, ez járható is. A mellékelt ábrán használt jelöléseket ajánlom. ( Hasonlóság miatt elég az ott látott AB szakasz esetén bizonyítani. ) A 38. feladat alapján először az APB és az ABC háromszög Euler-egyenese metszéspontjának meghatározását ajánlom. Szép, érdekes eredményt kapunk. Néhány nap múlva ezt közlöm.
|
 |
| Előzmény: [159] BohnerGéza, 2004-09-13 08:51:57 |
|
|
| [167] newbee | 2004-10-01 17:28:05 |
 Sziasztok!
bocs a zavarasert, pici segitseget szeretnek kerni affin transzformacikkal kapcsolatban. Eleg volna egy link is, ahol esetleg elmagyarazzak hogyan kell megszerkeszteni, de az is, ha cimszavakban elmeselitek.
Olyant kellene csinalnom, hogy adott egy haromszog, az affinitas iranya parhuzamos a tengellyel, es az egymasnak megfelelo pontok egy oldalra kerulnek. A masik: ugyanezen haromszog ferde affin kepe. A tengely nem metszi a haromszoget, es az egymasnak megfelelo pontok egy oldalon vannak.
Koszi :)
|
|
| [166] Hraskó András | 2004-09-29 03:16:57 |
 A legfrissebb Kömalban olvasható egy-egy szép megoldás a B.3678. és a B.3680. feladatra. Mind a két feladatra adható frappáns projektív geometriai gondolatmenet, amivel pld az utóbbi feladat állítását messzemenően általánosítani is lehet. Talán a PÁLYÁZAT-on is sikerrel indulhat az, aki megtalálja ezeket a megoldásokat.
|
|
|
|
| [163] nadorp | 2004-09-15 14:44:34 |
 Az ábra nem túl szép,de arra fogok hivatkozni.Nyilván AE=r. Könnyen látható, hogy O1G=1-2r és O1O2=2r. Innen a Pitagorasz-tétel szerint  . Végül, mivel ABC . Végül, mivel ABC =45o és BO1 szakasz nyilván szögfelező,ezért =45o és BO1 szakasz nyilván szögfelező,ezért  . Azt kaptuk tehát, hogy . Azt kaptuk tehát, hogy



Innen csak a kisebb gyök jó r<1 miatt,azaz

(Na én erre mondtam, hogy egy kicsit csúnya,de hát ez van)
|
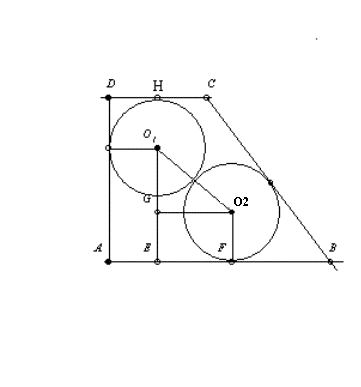 |
| Előzmény: [162] Hajba Károly, 2004-09-15 13:30:03 |
|
| [162] Hajba Károly | 2004-09-15 13:30:03 |
 Kedves Péter!
Mit nevezünk rondának? Az én megoldásomban a tört számlálójában, nevezőjében is van gyök, sőt a számlálóban gyökön belül még egy gyök. :o)
Írd be a megoldásodat és megbeszéljük.
HK
|
| Előzmény: [161] nadorp, 2004-09-15 12:11:58 |
|
|
| [160] Hajba Károly | 2004-09-13 10:21:59 |
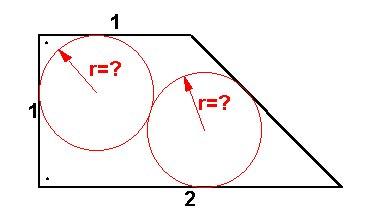
 39. feladat:
Mennyi az ábra szerinti egyforma, a trapézt 2 helyen s egymást is érintő körök r sugara?
HK
|
 |
|
| [159] BohnerGéza | 2004-09-13 08:51:57 |
 38. feladat: Igazoljuk az előző hozzászólásban a 'ha van igazság'-ban leírtakat, feltételezve, hogy a 37. feladat állítása igaz! ( Ezért is szép a geometria!)
|
|
| [158] BohnerGéza | 2004-09-08 20:25:06 |
 Egy ábra és megjegyzés a 37. feladathoz. (Bocs, a P az a pont, amiből a zöld vonalak indulnak.)
Ha van igazság, akkor az ABC háromszög Euler-egyenese is átmegy a többiek metszéspontján és akkor is igaz mindez, ha C-nél 120 fok van.
|
 |
|
| [157] BohnerGéza | 2004-08-13 12:40:42 |
 37. feladat: Az ABC háromszögben C-nél 60 fokos szög van. Legyen k a körülírt kör tükörképe AB-re és P legyen k-n! Igazoljuk, hogy az ABP, BCP és CAP háromszögek Euler-egyenesei egy pontban metszik egymást! (A megoldásával érdemben még nem foglalkoztam.)
Megjegyzés: A feladathoz a GEOMETRIA téma 2. feladata és a KÖMAL 2003 szeptemberi számának A.323. feladata adta az ötletet. Ujjgyakorlatnak jó a következő: 37./b feladat: Tetszőleges ABC esetén legyen P a körülírt kör középpontja! Igazoljuk, hogy az ABP, BCP és CAP háromszögek Euler-egyenesei egy pontban metszik egymást!
|
|
| [156] lorytibi | 2004-07-20 21:16:08 |
 Köszönöm a megoldást!
Tényleg nem olyan nehéz a feladat, csak jól át kell gondolni, mert könnyen félreérthető. Nekem az okozott gondot, hogy feladat szövege kizárja-e, hogy csak háromszögek keletkezhetnek és távolabbi pontokat összekötve, az ilyen szakaszok feldarabolhatnak-e háromszögeket.
Mostmár rájöttem, hogy a metszéspontok újjab pontoknak tekinthetők.
|
| Előzmény: [154] Sirpi, 2004-07-20 12:48:37 |
|
| [155] Kós Géza | 2004-07-20 21:12:51 |
 A szögek összeszámolása is működik.
A kis háromszögek szögeit kétféleképpen számolhatjuk össze: csúcsonként és háromszögenként. Legyen a belső pontok száma b. A szögek összege minden belső pont körül 360o; a nagy háromszög csúcsainál összesen 180o. Az összes kis háromszög összes szögének összege tehát b.360o+180o=(2b+1).180o, a kis háromszögek száma pedig 2b+1, ami páratlan.
|
| Előzmény: [154] Sirpi, 2004-07-20 12:48:37 |
|
| [154] Sirpi | 2004-07-20 12:48:37 |
 Szerintem nem olyan nehéz a feladat...
Tegyük fel, hogy a pontok segítségével h darab háromszögre bontottuk a nagy háromszöget, miközben a háromszög belsejében keletkezett e db él. Mivel belső pontokról van szó, ezért a nagy háromszög oldalai nem osztódtak tovább. Ekkor a háromszög éleinek száma kétféleképpen:
egyrészt 3h
másrészr 3+2e, mert a 3 nagy háromszögélt 1-szer, a belsőket kétszer számoltuk
Innen rögtön következik, hogy h páratlan, vagyis nem lehet 2004.
Ha a határon is lehetnek pontok, akkor nem megy ez a bizonyítás, de akkor meg triviálisan keletkezhet 2004 db. háromszög, pl. egy belső pontot összekötünk a 3 csúccsal, meg 2001 felvett határponttal.
|
| Előzmény: [153] lorytibi, 2004-07-20 12:01:48 |
|
| [153] lorytibi | 2004-07-20 12:01:48 |
 36.feladat: Egy háromszög belsejébe felveszünk pontokat. Majd a pontokat összekötjük egymással és a háromszög csúcsaival, úgy hogy háromszögek keletkezzenek. Bizonyítsuk be, hogy így nem keletkezhet 2004 darab háromszög!
A feladatot nekem egy matektábor pontversenyén adták fel, és elég keménynek bizonyult számomra.
|
|
| [152] BohnerGéza | 2004-07-18 12:40:02 |
 A 35. feladat megoldható tisztán vektorokkal, felhasználva azt, hogy a háromszög körülírt körének kp-jából a csúcsokba mutató vektorok összege a magasságpontba mutat. ( Rögzített kezdőpont esetén egy pontba mutató helyvektort - célszerűen - nagybetűs vektorral jelölöm.) A [150] hozzászólás ábráját használom. Legyen O a helyvektorok kp-ja, ekkor
|
 |
|
|
| [150] lorantfy | 2004-07-15 20:18:25 |
 Szia Sirpi!
Gratulálok, nagyon szép a megoldásod! Én is foglalkoztam vele és arra rájöttem, hogy tükörképe lesz (egy ábra alapján ez nem nagy szám), de nem tudtam bebiz.
A tükrözés P középpontja a körülírt kör O középpontjának az S súlypontra vonatkozó tükörképe lesz.
|
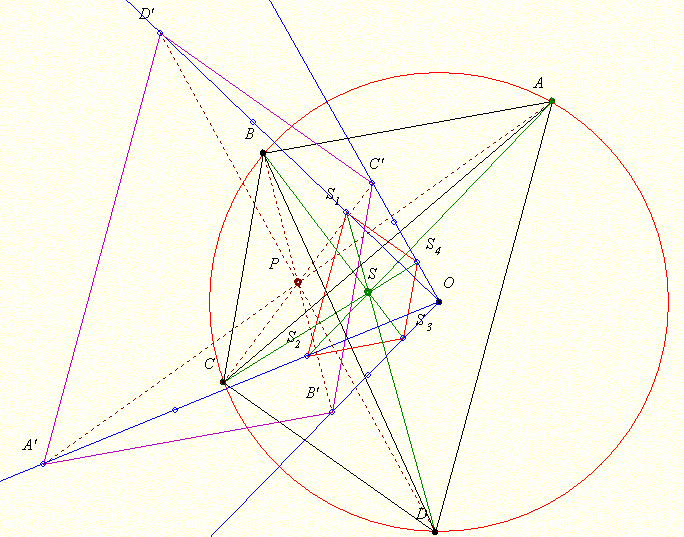 |
| Előzmény: [149] Sirpi, 2004-07-15 16:38:55 |
|
| [149] Sirpi | 2004-07-15 16:38:55 |
 Kollégámmal való hosszú fejtörés után sikerült egy frappáns megoldást találnunk.
Nözzük meg először, mit kapunk, ha magasságpontok helyett a súlypontokat vizsgáljuk. Ehhez vegyünk fel egy koordinátarendszert, melynek origója a húrnégyszög súlypontja, a csúcsok helyvektorai pedig rendre a, b, c, d, ezen vektorok összege 0, mivel az átlaguk a súlypont, ami az origóban van.
Ekkor a BCD háromszög súlypontja  , vagyis a súlypontok által meghatározott négyszög az eredetinek az origóból vett -3-szoros kicsinyitéséből kapható meg. , vagyis a súlypontok által meghatározott négyszög az eredetinek az origóból vett -3-szoros kicsinyitéséből kapható meg.
De miért is jó ez nekünk? Azért, mert most fel tudjuk használni a háromszögek Euler-egyenesére vonatkozó ismereteket, nevezetesen, hogy minden háromszögben a körülírt kör középpontja (O), a súlypont (S) és a magasságpont (M) egy egyenesen vannak, és távolságarányuk is állandó: 2OS=SM.
Mivel húrnégyszögről van szó, ezért a 4 kisháromszög körülírt köreinek középpontjai egybeesnek. A súlyponti háromszögekről tudjuk, hogy a négyszög súlypontjából való -3-szoros kicsinyítéssel kaphatók meg a nagy négyszögből. Az Euler-egyenes tulajdonságainak felhasználásával pedig azt kapjuk, hogy ha most O-ból a 3-szorosára nagyítjuk a súlypontok által alkotott négyszöget, akkor megkapjuk a magasságpontok által alkotottat.
Összegzésképpen: a magasságpontok által alkotott négyszög egybevágó az eredeti húrnégyszöggel, és annak középpontos tükörképe. Pótkérdés: mi a tükrözés középpontja?
|
| Előzmény: [148] lorybetti, 2004-07-14 18:58:50 |
|
| [148] lorybetti | 2004-07-14 18:58:50 |
 35.feladat:
Bizonyítandó, hogy egy húrnégyszög bármely 3 csúcsa által meghatározott háromszögek magasságpontjai az eredetihez hasonló négyszöget határoznak meg!
A feladat nehézségéről nem tudok nyilatkozni, annyit elárulok, hogy 11. osztályosoknak tűzték ki. Nekem okozott egy-két kellemes délutáni órát..
|
|
| [147] BohnerGéza | 2004-06-14 14:07:31 |
 Csak hogy a nyárra ne maradjon, akkor pihenjünk! A 32. feladat egy megoldása: A talpponti háromszög az eredetiből ahhoz hasonló, fordított körüljárású három háromszöget hagy meg, így ATbTc hasonló ABC-hez. Ezért, ha L-lel jelöljük az ABC beírt körének metszéspontját, AO / AL = ATb / AB. Tükrözzük L-t az AB-re: L’. Ekkor L’AO szög alfa és L’A=LA miatt (AO / AL’ = ATb / AB) AL’O hasonló ABTb-hez, AL’O szög = ABTb szög és O-nál derékszög van. Az AL’ Thalész-körén van O és Co, ezért ACoO szög = AL’O szög (= ABTb szög), tehát CoO merőleges AC-re, azaz O azonos M-mel.
Megjegyzés: Érdemes foglalkozni azzal az esettel, ha tompaszögű a háromszög, illetve a 32.b feladattal is ([138] [140] hozzászólások).
|
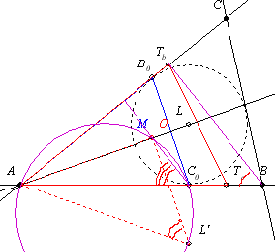 |
| Előzmény: [138] BohnerGéza, 2004-05-04 12:58:42 |
|
| [146] Hajba Károly | 2004-06-10 13:27:05 |
 Kedves Csimby!
Gratulálok, szép munkát végeztél. Írj erről egy nagyobb cikket, s beszéld rá Gézát, hogy tegye be a lapba. Így publikálva lesz, Tied az elsőség, ha más még nem foglalkozatt vele. :o)
Illetve fordítsd le angolra is és jelezz Eriknek.
Én akkor februárban foglalkoztam egy kicsit vele, de az elméleti hátterével nem. Habár Grafok vannak a családomban, a matematika eme területén csak kissé vagyok jártas. :o) Készítettem egy 60 elemes napsugaras változatot ill. papíron kerestem a 6 és 8 elemes változatot. Most már tudom, miért eredménytelenül. :o)
Vannak olyan problémafelvetések, melyek a felvetőnek nagyon érdekes, de mást vagy nem érdekel vagy nem ért annyira hozzá, így elsikkad. Nekem ilyen az egységnégyzet 11 egy kisebb négyzetre történő osztása, azaz hányféleképpen lehet felosztani 11 kisnégyzetre. Többször felvetettem, de senki nem reagált rá. Erre mondja a francia: C'est la vie!
Üdv: HK
|
| Előzmény: [145] Csimby, 2004-06-10 03:04:46 |
|
| [145] Csimby | 2004-06-10 03:04:46 |
 A 15. feladatra (65. hozzászólás) senki sem reagált, pedig szerintem érdekes problémakör. Akit mégis érdekelne a megoldás, csináltam egy honlapot ahol elég sok eredmény fenn van. Van amit elbonyolítottam és van amit nem bizonyítottam, tehát ha valakinek bármi észrevétele van, írjon. Mégegyszer a feladat: Milyen n esetén lehet n db. egybevágó négyzetet úgy elhelyezni a síkban, hogy mindegyik pontosan 3 másikat érintsen és az alakzat összefüggő legyen (érintésnek tekintjük azt is amikor a négyzetek csak egy pontban érintkeznek).
|
|
| [144] BohnerGéza | 2004-06-08 14:13:29 |
 Két ötlet a 34. feladat megoldásához:
1. Tekintsük a BCD körülírt körét, igazoljuk hogy e-vel való metszéspontja E! (Ebben az esetben van értelme a D ne lehessen C feltételnek, ennek hiányában ezt az esetet külön kellene vizsgálni. A második esetben nem kell a feltétel.)
2. Forgassunk B körül –60 fokkal! AC képe e lesz, így D képe e-re esik, igazoljuk, hogy ez E!
A 33. feladat megoldását mindenkinek javaslom (akár 7. osztályos kortól), aki tud a trapéz középvonaláról: a középvonal a párhuzamos oldalak számtani közepe. (2k=a+c)
|
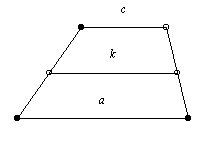 |
|
| [143] BohnerGéza | 2004-06-01 14:06:25 |
 A [46]-ban kitűzött 14. feladat egy megoldása: Tudjuk, hogy AB || CD és AX || CY, bizonyítadó, DX || YB. Jelölje a szárak metszéspontját P! A párh. szelők tételéből és megfordításából következik:
Tudjuk: (1.) PD/PA=PC/PB (2.) PA/PY=PX/PC.
Elég: PD/PY=PX/PB, amit (1.) és (2.) megfelelő oldalainak összeszorzásával meg is kapunk.
Megjegyzés: A [46]-ban kitűzött feladat megoldása szerepelt a [57], [62] és [mostani - kb. 3] hozzászólásokban, érdemes mindegyikkel foglalkozni.
|
|
| [142] lorantfy | 2004-05-19 16:51:28 |
 Kedves Géza!
Kösz a megoldást! Pontosan így gondoltam. Ha már hozzászólok beírok egy egyszerű kis példát is:
34. feladat: ABC egyenlő oldalú  C csúcsában húzzunk párhuzamost az AB oldallal, legyen ez e. Az AC oldal egyenesén vegyünk fel egy C-től különböző D pontot. BD szakasz felező merőlegese az e egyenest E-ben metszi. Bbh. BDE C csúcsában húzzunk párhuzamost az AB oldallal, legyen ez e. Az AC oldal egyenesén vegyünk fel egy C-től különböző D pontot. BD szakasz felező merőlegese az e egyenest E-ben metszi. Bbh. BDE  is szabályos! is szabályos!
|
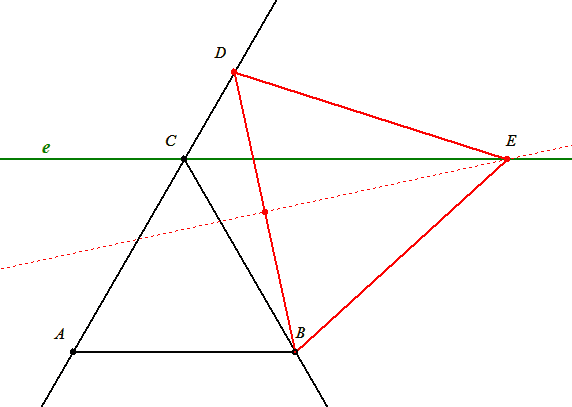 |
| Előzmény: [141] BohnerGéza, 2004-05-18 21:52:48 |
|
| [141] BohnerGéza | 2004-05-18 21:52:48 |
 A 14. feladat egy megoldása: Eredetileg így szól: (ne kelljen most megkeresni!) Vegyük fel az ABCD trapéz AD szárán az X, BC szárán az Y pontot. Bbh. ha AY párhuzamos CX egyenessel, akkor DY is párhuzamos BX egyenessel!
Alkalmazzuk a Pappos-tételt, mely például szerepel a [137]-es hozzászólásban. Használjuk ennek jelöléseit! Tehát az eredeti A legyen A, B-->C’, C-->A’, D-->C, X-->B és Y-->B’! Tudjuk, hogy AC’ és A’C valamint AB’ és A’B metszéspontja az ideális egyenesen van, a BC’ és C’B is ott kell messe egymást, tehát párhuzamossak.
|
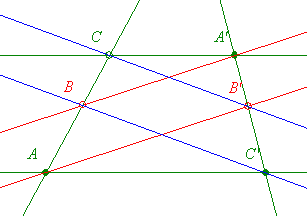 |
| Előzmény: [46] lorantfy, 2004-02-07 00:15:18 |
|
| [140] BohnerGéza | 2004-05-17 14:20:00 |
 Mivel igen leállt most a fórum: A 32. feladatról:
A feladatot a http://matek.fazekas.hu/portal/kutatomunkak/Feuerbach/index.html cikkből vettem. Érdemes tanulmányozni az ottani megoldást (és az egész hónlapot), de sokkal „szebbet” is lehet találni. A 32. b) feladathoz: Ha beírt kör szerepel egy feladatban, mindig érdemes lehet a hozzáírt körrel kapcsolatban az analógiát keresni ( és az Euklidesszel ellenőrizni a sejtést).
A [62.] hozzászólásban megígértem, hogy a [46] 14. feladatára adok ( a kitűzőnek tetsző ) megoldást. Mivel eddig más ezt nem tette meg, nekiállok.
|
|
| [139] lorantfy | 2004-05-09 15:12:01 |
 Kedves Géza és Fórumosok!
Bár a 30-31-es feladatot még nem oldottam meg, de tanulmányozása során találtam egy egyszerűen bizonyítható állítást:
33. feladat: Legyen két egymást O-ban metsző f és f’ egyenesünk egyikén az A, B és C pont, másikán az A’, B’ és C’. Legyen AB' és BA' metszéspontja D, BC' és CB' metszéspontja pedig F. Ha AB=BC és A’B’=B’C’ akkor
TAA'D+TCC'F=TBDB'F
|
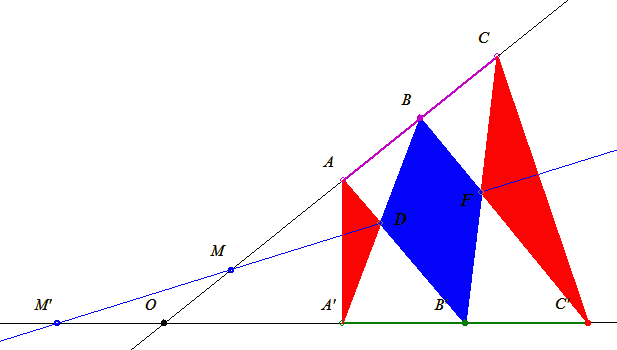 |
| Előzmény: [137] BohnerGéza, 2004-04-30 14:07:27 |
|
| [138] BohnerGéza | 2004-05-04 12:58:42 |
 32. feladat: Az ABC háromszögben a beírt kör érintési pontjai, ill. a magasságok talppontjai az AB ill. AC oldalon Co és Tc ill. Bo és Tb. Legyen M az ACoBo magasságpontja és O az ATcTb beírt körének középpontja. Igazoljuk, hogy O és M egybeesik.
32. b) feladat: Mondjuk ki és igazoljuk a 32. feladatnak megfelelő (analóg) feladatot.
A 31. b) feladat megoldásához: vektorok segítségével megy, ha jól választjuk meg az indulást, nem is túl sok számolás. Nagy örömmel látnék nem vektoros és nem koordinátageometriai megoldást is. Tanulnék belőle, mert egyelőre nem tudom, hogy kezdjek neki!
|
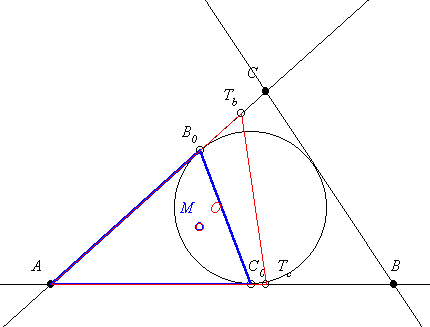 |
|
| [137] BohnerGéza | 2004-04-30 14:07:27 |
 A [128]-as hozzászólásában László felvetett egy problémát, amellyel érdemes foglalkozni. Legyen két egymást O-ban metsző f és f’ egyenesünk egyikén az A, B és C pont, másikán az A’, B’ és C’. Papposz tétele szerint az AB’ és A’B, az AC’ és A’C valamint a BC’ és B’C által meghatározott metszéspontok egy egyenesen vannak, jelöljük ezt g-vel. László fölveti a következőt:
30. a) feladat: Ha AB=BC=A’B’=B’C’, akkor g párhuzamos a két egyenes szögfelezőjével.
Egyenértékű ezzel a következő állítás: 30. b) feladat: Ha valamelyik ponthármast (pl. A-t B-t és C-t) az egyenesén a fenti feltételt tartva mozgatjuk, akkor a „g”-k párhuzamosak lesznek.
Az előző feladatok általánosítása a következő:
31. a) feladat: Ha AB=BC=e és A’B’=B’C’=e’, akkor ha valamelyik ponthármast (pl. A-t B-t és C-t) az egyenesén a feltételt tartva mozgatjuk, akkor a „g”-k párhuzamosak lesznek.
31. b) feladat: Ha g f-et egy M-ben f’-t egy M’-ben metszi, akkor OM:OM’=e:e’, valamint g csakkor halad át O-n, ha OB:OB’=e:e’.
Bocs, minden feladat akkor lesz az, ha hozzátesszük, hogy bizonyítandó!
|
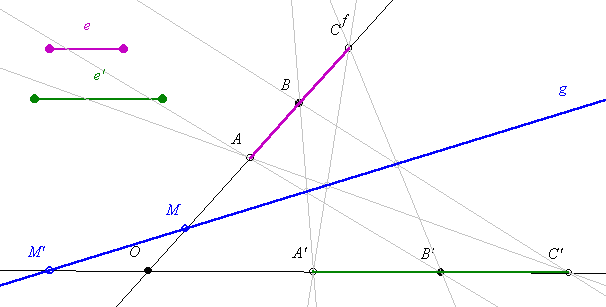 |
| Előzmény: [128] lorantfy, 2004-04-27 14:19:02 |
|
| [136] lorantfy | 2004-04-29 23:43:15 |
 Kedves NádorP, Géza és Fórumosok!
Jogos volt Géza bírálata, [131]-ben mindenütt "<" jeleket kellett volna írnom. "Lehet látni", hogy  növekedésével az arány 2-höz tart, de az kevés! Nagyon elegáns NádorP bizonyítása. Akit érdekel a területeknél használt képlet a Versenyfeladatok témában NádorP [16] hozzászólásában utánna nézhet. növekedésével az arány 2-höz tart, de az kevés! Nagyon elegáns NádorP bizonyítása. Akit érdekel a területeknél használt képlet a Versenyfeladatok témában NádorP [16] hozzászólásában utánna nézhet.
A szintén ott említett Jensen egyenlőtlenséghez már akkor fel akartam tenni egy ábrát, most megteszem, mert itt is előjön. ( Ha jól megnézitek, látható, hogy ez nem cos fgv. hanem egy parabola. Bocs! Euklidesben ezt egyszerűbb rajzolni.)
|
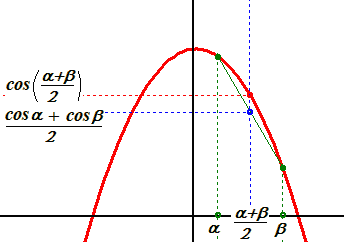 |
| Előzmény: [135] nadorp, 2004-04-29 16:25:58 |
|
|
| [134] Hajba Károly | 2004-04-27 23:04:03 |
 Kedves Géza és László!
Én is közreadom a megoldásomat a 28. feladatra:
Az f szakasz tetszőleges P pontjára állított merőleges Q-t metszi ki e-ből. Erre a pontra állított merőleges pedig R-t metszi ki f-ből. P-t Q körül a QR szakaszra forgatva kimetszi S-t. Q-ból PS-re bocsátott merőleges T-t metszi ki f-ből. PQS egyenlő szárű háromszög hasonló TOQ egyenlő szárű háromszög hasonló TOQ -gel és egymásra merőlegesek, ahol O az e és f szakaszok meghosszabbításának metszéspontja. Így a QT szakaszfelező merőlegese átmegy O-n, azaz a kivánt szakaszfelező. -gel és egymásra merőlegesek, ahol O az e és f szakaszok meghosszabbításának metszéspontja. Így a QT szakaszfelező merőlegese átmegy O-n, azaz a kivánt szakaszfelező.
Direkt szakaszokat írtam, ezzel is példázva, hogy nem kell O-t felhasználni.
HK
|
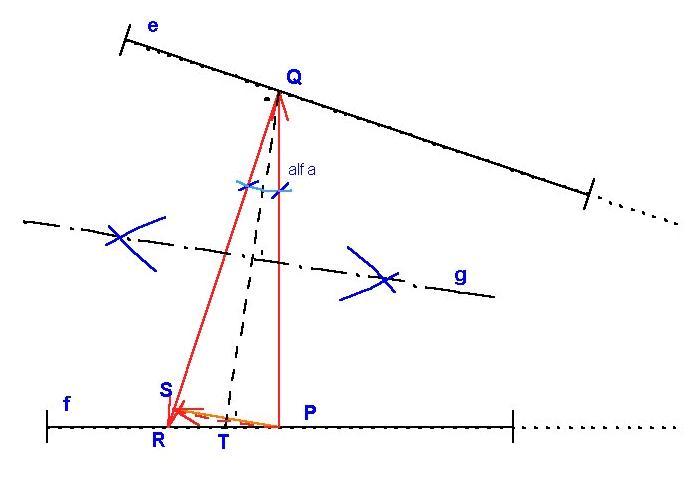 |
| Előzmény: [130] lorantfy, 2004-04-27 18:31:12 |
|
| [133] BohnerGéza | 2004-04-27 22:11:46 |
 Kedves László!
Kicsit fáradt vagyok, különben az előző hozzászólásomban a megszólításra és a megoldásod fölösleges bírálatára is jobban figyeltem volna, hiszen semmi baj nincs vele, nyugodtan elhagyható az egyenlőség.
|
| Előzmény: [132] BohnerGéza, 2004-04-27 21:58:46 |
|
| [132] BohnerGéza | 2004-04-27 21:58:46 |
 Kedves Laci és Fórumosok!
Az Euklideszben az index beírása A&1 formában lehetséges.
Nagyon szép és tanulságos a 29. feladatra írt megoldásod. Kicsit szépséghibája, hogy az egyenlőséget nem megengedve is igaz. Ha a területek 0-hoz tartanak lesz az arány határértéke kettő. Érdemes lehet a feladatot megfogalmazni a következő általánosabb formában: Egy talpponti háromszög és az eredeti háromszög területének arányát tekintsük negatívnak, ha a háromszög tompaszögű. ekkor igaz a -2<arány<=1/4.
|
| Előzmény: [131] lorantfy, 2004-04-27 21:13:37 |
|
|
