| [41] Róka Sándor | 2024-07-14 22:22:50 |
 Két új kérdés.
6. kérdés: Legfeljebb hány királynő helyezhető el a sakktáblán úgy, hogy mindegyik legfeljebb egy másikat tartson ütés alatt?
7. kérdés: Dagobert bácsinak van 10 bankkártyája, melyeken 1, 2, 3, ..., 10 ezer dollár van. Szegény már elfelejtette, hogy ezek melyik kártyán vannak, csak a pénzösszegekre emlékszik. Mindegyik kártya csak egyszer használható. Dagobert bedughatja a kártyát az ATM-be, és kérhet valamilyen összeget. Ha van rá fedezet, az ATM kiadja a kért pénzösszeget, különben nem ad ki semmit. Sajnos az ATM nem mutatja meg, hogy mennyi pénz volt a kártyán. Mekkora az a legnagyobb összeg, amit Dagobert bácsi biztosan fel tud venni a kártyákról?
|
| Előzmény: [22] Róka Sándor, 2024-07-07 09:17:06 |
|
| [40] Makay Géza | 2024-07-14 19:01:17 |
 Most írom a 4. kérdésre a választ... :)
Az 5 bástya lefog 5 sort és 5 oszlopot a táblából. 3 sor és 3 oszlop marad szabad, ahová egyáltalán el lehet helyezni huszárt. Így legfeljebb \(\displaystyle 3\times 3=9\) huszárt lehet elhelyezni, az pedig lehetséges is:
|
 |
| Előzmény: [22] Róka Sándor, 2024-07-07 09:17:06 |
|
|
| [38] Makay Géza | 2024-07-14 13:53:58 |
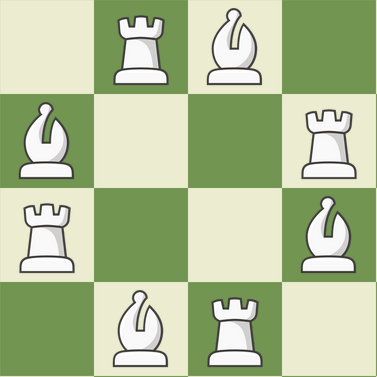
 4. kérdés. Mivel a bástya által ütött két futó nem lehet ugyanaz a két futó, ami üti a bástyát, ezért legalább 4 futó van. A szerepeket felcserélve is okoskodhatnánk, de mivel ugyanannyi bástya és futó van, ezért legalább négy bástyának is lennie kell. És erre itt egy lehetséges elhelyezés:
|
 |
| Előzmény: [22] Róka Sándor, 2024-07-07 09:17:06 |
|
| [37] Makay Géza | 2024-07-14 12:45:03 |
 Ez alapján 3 "szabad" rácspontunk van, amit nem muszáj lefednünk. Így nem lehet minden sarok üres, mert az 4 nem lefedett rácspontot jelentene. Nem lehet mind a 4 sarokban egymást átlósan ütő király-pár, mert az is 4 plusz rácspontot igényelne. 0 vagy 2 olyan király lehet, amelyik nem üt másikat, hiszen egy király önmagában 4 rácspontot foglal el. Ezek alapján kell legyen egy olyan sarok, amelyben két király oldalszomszédos mezőn áll. Forgatással és tükrözéssel megoldható, hogy ezek a bal felső sarokban az első sorban álljanak. Ha ehhez hozzávenném, hogy nyilvántartsam a "kihagyott" rácspontokat, akkor a program valószínűleg záros határidőn belül lefutna.
Másik ötlet a fentiek alapján, hogy a király-párokat igyekszem lerakni. Alapvetően nem sok eset lehet:
1. Minden pár oldalszomszédos: 3 rácspont marad ki.
2. Két egyedülálló király van (mint pl. a 27-es hozzászólásban), a többi oldalszomszédos: 1 rácspont marad ki.
3. Két egyedülálló király van, egy átlósan ütő pár, a többi oldalszomszédos: nincs kimaradó rácspont.
4. Egy, kettő vagy három átlósan ütő pár van, a többi oldalszomszédos: 2, 1 vagy 0 rácspont marad ki.
Mivel főleg király-párokat helyezünk el, a vizsgálandó esetek száma óriásit csökken, ez szerintem másodperceken belül meg kell adja az összes megoldást, bár leprogramozni bonyolultabb (valakinek nincs kedve megcsinálni? :) ). Amúgy szerintem a 3. pont és a 4. pontból az utolsó kettő nem fog előfordulni.
|
| Előzmény: [34] Róka Sándor, 2024-07-13 20:54:06 |
|
| [36] Makay Géza | 2024-07-14 12:06:32 |
 Kiszűrtem a forgatással/tükrözéssel egymásból megkapható megoldásokat és pár perc futás után találtam 156 megoldást. A programom nem nézte végig (valószínűleg ebben a formában nem is tudja végignézni) az összes lehetséges megoldást, így nem tudom, hogy ez mennyire van "közel" az összeshez...
|
| Előzmény: [29] sakkmath, 2024-07-12 22:14:03 |
|
|
| [34] Róka Sándor | 2024-07-13 20:54:06 |
 Miért nem lehet 26-nál több királyt elhelyezni a táblán?
Figyeljük az "elfoglalt" rácspontokat.
A sakktáblán a rácsegyenesek \(\displaystyle 9\cdot9=81\) pontban metszik egymást, 81 rácspont van.
2 egymást ütő király 6 vagy 7 rácspontot foglal el. Ha 2 másik ilyen királyt nézünk, azokhoz más rácspontok tartoznak. Ha a 26 király 13 párt alkot (az egy párban lévők ütik egymást), akkor ők legalább \(\displaystyle 13\cdot6=78\) rácspontot foglalnak el a 81-ből ...
|
| Előzmény: [24] Makay Géza, 2024-07-12 12:02:14 |
|
|
|
|
|
| [29] sakkmath | 2024-07-12 22:14:03 |
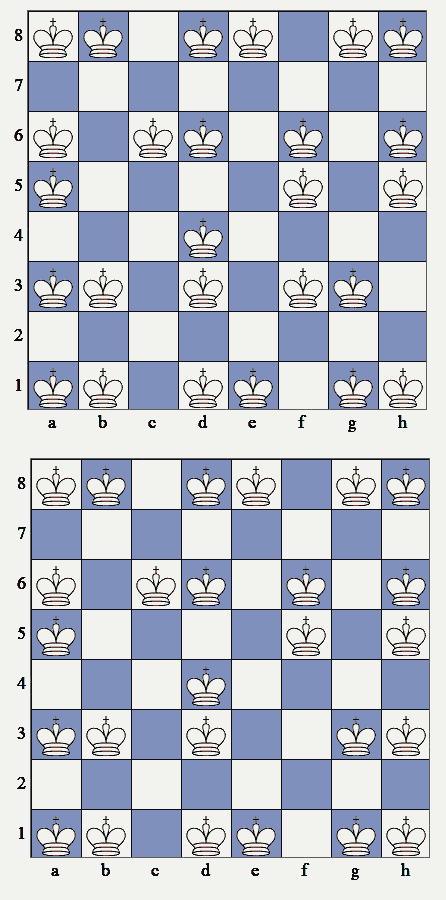
 Újabb két megoldás alul.
24/b. feladat:
Hány különböző megoldása van a feladatnak, ha eltekintünk a (tengelyes-, vagy középpontos) tükrözésekből adódó többletmegoldásoktól?
|
 |
| Előzmény: [28] Káli gúla, 2024-07-12 21:42:47 |
|
| [28] Káli gúla | 2024-07-12 21:42:47 |
 De talán ez a legjobb, mert a mintázat könnyen bővíthető minden \(\displaystyle 6k+2\) oldalú táblára. Sőt, minden páros \(\displaystyle n\)-ről \(\displaystyle (n+6)\)-ra.
|
 |
|
|
| [26] S.Ákos | 2024-07-12 20:52:34 |
 Szerintem erre gondolt a kolto:
Ka1,Kb1,Kd1,Ke1,Kg1,Kh1,
Ka3,Kb3,Kd3,Ke3,Kg3,Kh3,
Ka5,Kb5,Kd5,Ke5,Kg5,Kh5,
Ka7,Ka8,Kc7,Kc8,Kf7,Kf8,Kh7,Kh8
|
 |
| Előzmény: [25] sakkmath, 2024-07-12 19:09:27 |
|
| [25] sakkmath | 2024-07-12 19:09:27 |
 Soraidból sajnos nem tudom egyértelműen beazonosítani a programod megoldását/megoldásait. Örülnék, ha ezt/ezeket vagy ábrán, vagy koordinátázva bemutatnád, vagy leírnád.
|
| Előzmény: [24] Makay Géza, 2024-07-12 12:02:14 |
|
|
| [23] Káli gúla | 2024-07-07 10:40:44 |
 A lövős analógia a futókra is használható. A sarkokat ferdén levágjuk, így lesz 28 falszakasz. A többi szélső mezőről (24) legalább 1 falszakasz látható, a többi mezőről már 4-felé lehet lőni, ami már bábunként 2-2 új falszakaszt jelent. És a 4 sarokfalat lehet is támadni 1-1 átlómezőről.
|
 |
| Előzmény: [21] Róka Sándor, 2024-07-06 20:40:30 |
|
| [22] Róka Sándor | 2024-07-07 09:17:06 |
 Újabb kérdések:
3. kérdés: Legfeljebb hány király állhat a sakktáblán, ha mindegyik legfeljebb egy másikat tart ütés alatt?
4. kérdés: A sakktáblán 5 bástya és néhány huszár áll úgy, hogy egyik bábu sem üti valamely másikat. Legfeljebb hány huszár van a táblán?
5. kérdés: Legkevesebb hány bástya és hány futó áll a sakktáblán, ha mindegyik bástya legalább két futót, illetve mindegyik futó legalább két bástyát támad, és ugyanannyi bástya van, mint futó?
|
| Előzmény: [3] Róka Sándor, 2024-07-02 14:04:12 |
|
| [21] Róka Sándor | 2024-07-06 20:40:30 |
 Emma kérdésére egy újabb megoldás.
Egy bástya 4 irányban „lő”, és a tábla széleit összesen legfeljebb 32 lövés éri. Legyen a bástyák száma \(\displaystyle x\).
Ha minden bástya két másikat tart ütés alatt, akkor 2 „lövése” éri a falat, így \(\displaystyle 2x\le 32\) tehát a bástyák száma legfeljebb 16 lehet.
16 bástya elhelyezhető a táblán, lásd a 6. hozzászólást. A 16 bástyát elhelyezhetjük így is:
|
 |
| Előzmény: [7] UdvariTibor, 2024-07-02 18:23:50 |
|
| [20] Róka Sándor | 2024-07-05 17:40:24 |
 Köszönöm a fordulókhoz a linkeket, a feladatok/megoldások elérhetőségét.
Négy fordulóban is volt olyan feladat (9., 17., 24., 32. feladat), hogy bábukat pakolunk a sakktáblára, valamilyen szabályt betartva, minél többet. Ezek a sakktáblás feladatok segíthetnek új kérdéseket megfogalmazni. A 17-es meglepő módon azonos a gyomos feladattal (lásd F.3220, KöMaL), és ez egy különleges, érdekes feladat, feladatkör.
A 28-as feladathoz sokféle indoklás érkezett, szép ötletekkel, kisebb hiányosságokkal. Ezekről is lehetne itt a Fórumban beszélgetni. (Lásd még: F.2280, P.364, KöMaL)
A 23-asra érkezett egy káprázatos, 8 oldalas megoldás, ez cikk lehetne a KöMaL-ban. (Az általános eset vizsgálata közben bizonyítja az 1997-es IMO 6. feladatát.) Ebből a megoldásból sokat tanulhatunk, ..., ha láthatjuk. Ezt lehetővé teheti a Fórum.
Szándékunk, hogy a kitűzött feladatok megoldására egy érdeklődő tizenévesnek hasonló esélye legyen, mint egy nyugdíjas matematikatanárnak. (Vannak is beküldők mindkét csoportból.)
Évente négyszer jelenik meg új feladatsor, 2 hetes beküldési határidővel. A Fórum lehetőséget ad az aktivitásra a köztes időszakokban.
(Ha a Fórumban hosszabb ideig csend van, akkor követem a 2.hsz. tanácsát: "Javaslom, dobj be egy-egy konkrét feladatot, amit meg tudunk tárgyalni.")
|
| Előzmény: [19] Sinobi, 2024-07-05 11:20:33 |
|
|
| [18] Sinobi | 2024-07-05 11:11:08 |
 Moderátor, nem lehetne szétrobbantani ezt a témát kisebb témákra, minden fordulóra egy? És akkor a téma indítója tartalmazhatja a feladatokat is.
hsz 3-9,12-14 : 5. forduló
hsz 10,11,15,17 : nem héttusa
hsz 16 : 3. forduló
|
|
| [17] Káli gúla | 2024-07-04 22:34:54 |
 Feleltessünk meg a kártyáknak 3-dimenziós rácspontokat. A feladat olyan \(\displaystyle P,Q\) pontpárokat elkerülni, amelyekre \(\displaystyle PQ\) párhuzamos egy koordinátasíkkal, de nem párhuzamos egyik tengellyel sem. Úgy is fogalmazhatunk, hogy a rossz pontpár azonos rétegben van, de nincs egy vonalban (az ,,egy vonalban" kifejezés pontosan a Makay Géza által bevezetett blokk fogalmat jelenti).
Lássuk be teljes indukcióval, hogy az \(\displaystyle [n]\times [m]\times [h]\) (\(\displaystyle n,m,h\ge4\)) rácstéglában legfeljebb \(\displaystyle n+m+h-6\) pont vehető fel úgy, hogy ne legyen köztük rossz pontpár. Nézzük először a 4x4x4-es kockát, abban is a vízszintes (\(\displaystyle z=k, k=1..4\)) rétegeket. Tegyük fel, hogy van 7 pont a kockában, rossz pár nélkül.
\(\displaystyle \bullet\) Ha valamelyik rétegben 4 pont van, azok szükségképpen egy vonalban vannak, így minden \(\displaystyle x,y\) értékpárt lefednek, tehát egy további pont akármelyik rétegben ezek egyikével rossz párt alkotna.
\(\displaystyle \bullet\) Ha valamelyik rétegben 3 pont van – szükségképpen egy vonalban – akkor ebben a vonalban egy pont hiányzik, és minden további (tehát 4) pont a hiányzó \(\displaystyle x\) vagy \(\displaystyle y\) koordinátaértékhez tartozó, a vonalra merőleges függőleges rétegbe kell hogy essen, ami az előbbi miatt rossz párhoz vezet.
\(\displaystyle \bullet\) Végül, ha csak 3 vízszintes rétegben lenne pont, akkor valamelyik rétegbe legalább 3 pont jutna a 7-ből. Ez tehát nem lehet, és így feltehetjük, hogy mind a 4 rétegben van pont, méghozzá 2-2-2-1 elosztásban.
Legyenek ezeknek a vetületei a \(\displaystyle z=0\) síkon \(\displaystyle A,A'\), \(\displaystyle B,B'\), \(\displaystyle C,C'\) és \(\displaystyle D\). Könnyű látni, hogy \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) egy szabad bástyafelállásnak felel meg, azaz nincs közöttük kettő azonos vonalban, és nincs egybeesés sem, így ez a 4 pont minden \(\displaystyle x,y\) értékpárt lefed, tehát pl. az \(\displaystyle A'\)-nek megfelelő pont valamelyik vesszőtlen pont ősével rossz párt kell hogy alkosson. Ez pedig ellentmondás.
Tehát a 4x4x4-es kockában legfeljebb 6 megfelelő pont lehet. (Annyit meg is lehet adni, méghozzá különös módon kétféleképpen, amikor 3+3, illetve amikor 2+2+2 esik egy-egy kitérő vonalba.)
Az \(\displaystyle n+m+h\) szerinti teljes indukciós lépés nagyon egyszerű. Tekintsük a \(\displaystyle n,m,h\) közül a legnagyobbnak megfelelő irányt függőlegesnek. Ha így minden vízszintes rétegben legalább 2 pont van, akkor a párok vetületeiről ugyanazt mondhatnánk, mint a 4x4x4-es bizonyítás végén. Ezért valamelyik vízszintes rétegben legfeljebb 1 pont van, ezt a réteget elhagyva, alkalmazhatjuk az indukciós feltevést az eggyel kisebb téglára, és készen vagyunk.
|
| Előzmény: [15] Makay Géza, 2024-07-04 06:30:46 |
|
