| [736] Csimby | 2007-05-18 01:25:08 |
 Ez érdekes. Kontinuum sokra gondolom jó a c db pont :-) Megszámlálhatóan végtelenre meg talán kijön a véges esetből, de ehhez most késő van hogy végiggondoljam. De eredetileg véges sokra gondoltam (arra ismerek bizonyítást).
|
| Előzmény: [731] jonas, 2007-05-17 13:48:33 |
|
| [735] BohnerGéza | 2007-05-17 17:48:31 |
 Talán grab a [721]-ben nem fogalmazott pontosan, de mivel alapvetően a körön a vonalát értjük, és a szövegkörnyezetből sem következett más, tulajdonképpen a szabályos ötszög szerkesztéséről szólhatott a kérdés. ??????
Mivel sem Csimbi, sem grab nem adott ímélcímet, csak itt tudok rákérdezni.
|
| Előzmény: [723] Csimby, 2007-05-16 23:10:36 |
|
|
|
|
| [730] Yegreg | 2007-05-17 13:26:34 |
 2C-nél nem hiszem, hogy lehet több, mivel az összes ponthalmazok száma is 2C
|
|
| [733] Sirpi | 2007-05-17 08:30:32 |
 A [0;1) intervallum részhalmazaihoz mind hozzárendelhetünk egy-egy különböző konvex halmazt:
vegyünk egy 1 kerületű nyílt kört (a külső körív legyen 0 és 1 közt egyenletesen paraméterezve), és ehhez azokat a kerületi pontokat vegyük hozzá, amelyek benne vannak az intervallumunkban. Vagyis már legalább 2c-nél tartunk, nem tudom, lehet-e esetleg még többet.
Persze módosít(hat) a dolgon, ha csak zárt (vagy csak nyílt) konvex halmazokat engedünk meg.
|
| Előzmény: [729] Csimby, 2007-05-16 23:46:54 |
|
|
|
|
|
| [725] Csimby | 2007-05-16 23:23:03 |
 113. feladat Hány konvex halmaz van a síkon?
|
|
| [724] Csimby | 2007-05-16 23:14:06 |
 Amúgy,
4.feladat: Bontsunk fel egy kört egybevágó síkidomokra úgy, hogy legalább az egyik darab ne tartalmazza a kör középpontját, még határán sem.
Hátha valaki új a fórumon, vagy már nem emlékszik erre a feladatra.
|
| Előzmény: [10] Csimby, 2004-01-12 21:54:12 |
|
|
|
| [721] grab | 2007-05-16 21:03:33 |
 Sziasztok, abban szeretném a segítséget kérni ,hogy egy kör hogy oszthetó fel 5 részre?
|
|
|
|
| [718] Doom | 2007-05-14 23:53:54 |
 Szép, rövid megoldás. Nekem csak egyoldalas megoldást sikerült gyártanom, bár annak előnye, hogy szinte csak az addíciós tételeket felhasználva jut el a parabola általános képletéig.
|
| Előzmény: [716] Lóczi Lajos, 2007-05-14 23:41:06 |
|
|
| [716] Lóczi Lajos | 2007-05-14 23:41:06 |
 Felejtkezzünk el a zavaró konstansoktól: nyilván elég belátni, hogy a T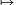 (sin (T),sin (T+c)) síkgörbe (T (sin (T),sin (T+c)) síkgörbe (T R) ellipszis, akárhogyan is választjuk meg a c valós paramétert. R) ellipszis, akárhogyan is választjuk meg a c valós paramétert.
Vegyük észre, hogy az X:=sin (T), Y:=sin (T+c) választással minden T-re és c-re fennáll az
X2+Y2-2cos (c).XY-sin2(c)=0
azonosság. Ha c olyan, hogy sin (c)=0, akkor a görbénk egy szakasz, ami elfajult ellipszis. Ha sin (c) 0, akkor viszont a http://mathworld.wolfram.com/Ellipse.html oldal (16)-(18)-as képlete alapján szintén ellipszist kapunk, hiszen esetünkben (az ottani jelölésekkel) 0, akkor viszont a http://mathworld.wolfram.com/Ellipse.html oldal (16)-(18)-as képlete alapján szintén ellipszist kapunk, hiszen esetünkben (az ottani jelölésekkel)  =-sin4(c) =-sin4(c) 0, J=1-cos2(c)>0 és I=2 miatt 0, J=1-cos2(c)>0 és I=2 miatt  /I<0. /I<0.
|
| Előzmény: [715] Doom, 2007-05-14 19:40:52 |
|
|
|
| [713] HoA | 2007-05-04 10:18:33 |
 [711] utolsó mondata alapján a 112. feladat: Az ABC háromszög AB oldalán szerkesszük meg azt a D pontot, melyre a CAD és CDB háromszögek beírt körei egyenlő sugarúak.
|
| Előzmény: [711] BohnerGéza, 2007-04-30 00:40:56 |
|
| [712] jenei.attila | 2007-04-30 18:55:00 |
 Köszi a segítséget. Így már persze sokkal könnyebb. Nem tudok ilyen szép ábrát rajzolni, de jelöljük a k1 kör és AB oldal érintési pontját M-mel, a k2 és AB érintési pontját N-nel. Mivel k1 a piros háromszög beírt köre, ezért GM=a piros háromszög félkerülete, mínusz ED. Mivel k2 a piros háromszög hozzáírt köre, GN=a piros háromszög félkerülete. Ebből ED=MN következik. Az ABC háromszög kerülete (az érintő szakaszok egyenlősége miatt) CP+CQ+DM+DN+2AM+2BN=CP+CQ+DQ+DP+2AM+2BN=2CD+2AM+2BN. Jelöljük az ABC háromszög félkerületét s-sel. Ekkor CD=s-AM-BN, és CE=CD-ED=s-AM-BN-ED=s-AM-BN-MN=s-AB
|
| Előzmény: [711] BohnerGéza, 2007-04-30 00:40:56 |
|
| [711] BohnerGéza | 2007-04-30 00:40:56 |
 A [654]-es hozzászólás és az itteni ábra remélem segít. A CE=s-c kell legyen, hiszen D-t pl. A-hoz közelítve E az ABC háromszög beírt körének Bo érintési pontjához közzelít. A k1 és k2 a piros háromszög be- ill. hozzáírt köre. Külön vizsgálandó, ha a két kör egyforma.
|
 |
| Előzmény: [710] jenei.attila, 2007-04-29 20:33:43 |
|
| [710] jenei.attila | 2007-04-29 20:33:43 |
 Íme egy Arany Dániel feladat, amit eddig nem tudtam megoldani: Az ABC háromszög C csúcsából kiinduló egyenes az AB szakaszt D pontban metszi. Legyenek a CAD és CDB háromszögek beírt körei k1 és k2. A két kör (AB-től különböző)külső érintője a CD szakaszt E pontban metszi. Bizonyítandó, hogy a CE szakasz hossza független a D pont választásától.
|
|
| [709] BohnerGéza | 2007-04-26 17:46:14 |
 Szép megfejtése annak, mire alkalmazható itt az inverzió! A [692]-ben Python szépen igazolta, hogy PQRS paralelogramma, a kettő együtt elég. A [708]-ban HoA által említett P'Q'R'S' négyszög érintő- húrnégyszög. ( kiderült, hogy lehet ilyet szerkeszteni.)
|
| Előzmény: [708] HoA, 2007-04-26 14:50:49 |
|
| [708] HoA | 2007-04-26 14:50:49 |
 Sajnos nekem csak ötlet! Odáig világos, hogy az ívek adott választása miatt az inverzióban a Thálesz körök képeiként adódó egyenesek által meghatározott P'Q'R'S' négyszög húrnégyszög, ezért PQRS is az. De a téglalaphoz még be kéne látni, hogy a szemben lévő oldalak párhuzamosak, vagy hogy a szomszédosak merőlegesek. Ez az inverzekre azt jelenti, hogy pl. a P'Q'O és R'S'O pontokon átmenő körök érintik egymást, illetve hogy pl. a P'Q'O és Q'R'O pontokon átmenő körök merőlegesen metszik egymást, ezekkel azonban nem boldogulok.
|
| Előzmény: [693] BohnerGéza, 2007-03-28 22:09:31 |
|
|
| [706] HoA | 2007-04-20 11:54:37 |
 Én úgy értelmeztem a feladato(ka)t, hogy ABCD ebben a sorrendben, pozitív körüljárás szerint van az oldalegyeneseken - és téglalap esetében az is adott, hogy A van a "b" hosszúságú oldalon. Ezért BD-nek csak pozitív 90 fokos elforgatottját vettem. Ez BohnerGéza megoldásának lila négyzete. Ha a fordított körüljárást is megengedem, és BD negatív 90 fokos elforgatottját mérem fel C-ből, akkor a zöld négyzetet kapom. Tovább bővül a megoldások száma, ha ABDC sorrend is megengedett. Ekkor persze az A-val szemközti oldalon D van, tehát BC elforgatottját kell D-ből felmérni. Ismét a két körüljárási irányt megengedve a pozitív 90 fokos elforgatottal adódik a piros, a negatívval a kék négyzet. Téglalap esetében még egy kettes szorzó jön be a megoldások számára, ha nem rögzítem, hogy A az "a" vagy a "b" oldalon van. Ez az én megoldásomban az elforgatott vektorok k -szorosának és 1/k -szorosának használatát jelenti, BohnerGéza ábráján pedig az átló hol az egyik hol a másik oldallal zárja be a k tangensű szöget.
|
| Előzmény: [705] BohnerGéza, 2007-04-19 20:29:32 |
|
| [705] BohnerGéza | 2007-04-19 20:29:32 |
 A 109. és 110. feladatra HoA által adott megoldásvázlat [696]-ban és [704]-ben a BD vektor + illetve -90 fokos forgatásával két megoldást ad. Helyes-e a [699]-ben felvázolt négy megoldás?
|
| Előzmény: [704] HoA, 2007-04-19 16:24:43 |
|
|
|
|
|
| [700] Python | 2007-04-16 07:14:02 |
 111. feladat Egy háromszögben két oldal és egy szögfelező háromszögön belüli szakasza is egyenlő hosszú. Mekkorák a háromszög szögei?
|
|
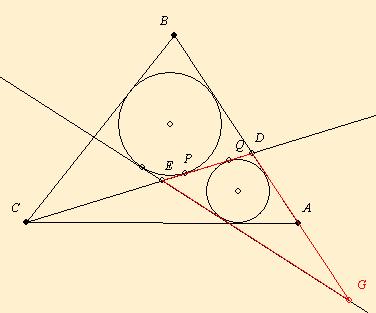
| [699] BohnerGéza | 2007-04-12 19:55:57 |
 A 109-es és 110-es feladatokhoz: A PQRS négyzet PQ oldalegenesén legyen A, QR-en B, RS-en C és SP-n a D. Ekkor Q számára vonal az AB és S számára a CD Thálesz-köre. Mivel az átló oldallal bezárt szögét is ismerjük, így az átlónak a körökkel való metszéspontja is ismert. Az ábrán a 109. feladat megoldása látszik, a piros és a lila pozitív körüljárású a négy mo. közül.
|
 |
| Előzmény: [691] lorantfy, 2007-03-28 11:33:35 |
|
|
| [697] jenei.attila | 2007-04-11 12:32:25 |
 Így egyszerűbb, de lényegében ugyanaz. A téglalappal kapcsolatban én 180 fokos elforgatásra gondoltam, de közben rájöttem hogy nem jó, mert A2 C-vel egybe fog esni, vagyis nincs A2-C egyenes.
|
| Előzmény: [696] HoA, 2007-04-11 11:21:03 |
|
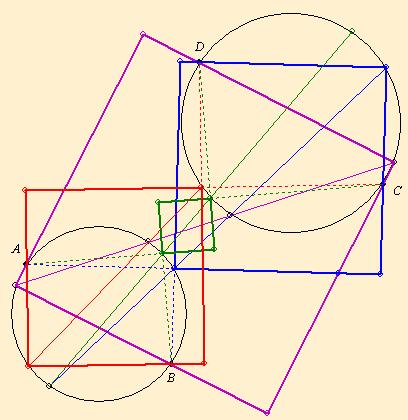
| [696] HoA | 2007-04-11 11:21:03 |
 Elég BD 90 fokos elforgatottját C -ből felmérni. A D1 végpont A-val közös oldalegyenesen van. Ezzel C-n át párhuzamost, B-n és D-n át merőlegest húzva készen vagyunk. (Amiből az is rögtön látszik, hogy a megoldás nem egyértelmű ha D1 A-ba esik, vagyis ha CA BD 90 fokos elforgatottja)
Téglalapra azért nem megy, mert kihasználtuk, hogy az "AC sáv" és a "BD sáv" egymás 90 fokos elforgatottjai, egyforma szélesek, ami téglalapra nem igaz.
|
 |
| Előzmény: [695] jenei.attila, 2007-04-11 10:19:52 |
|
| [695] jenei.attila | 2007-04-11 10:19:52 |
 Az adott pontok legyenek A,B,C,D. Forgassuk el ezeket tetszőleges pont körül 90 fokkal, az elforgatott pontokat A1,B1,C1,D1 jelöli. Alkalmazzunk az elforgatott pontokra egy eltolást, amely D1-et A-ba viszi. Az eltolt pontokat A2,B2,C2,D2 jelöli. Ekkor a C és B2 pontokat összekötő egyenes a négyzet egy oldalegyenese.
Nem biztos hogy jó ez a megoldás, mert adott négy ponttal téglalap szerkesztése nem egyértelmű. Holott hasonló logikával, csak a pontokat 180 fokkal elforgatva és C1-et A-ba vivő eltolással C-A2 egyenes egyértelműen megadja a téglalap egy oldalegyenesét. Még nem teljesen gondoltam végig, várom a hozzászólásokat.
|
| Előzmény: [691] lorantfy, 2007-03-28 11:33:35 |
|
| [694] Python | 2007-04-05 17:43:41 |
 109. megvan, egy eltolás meg egy forgatás, csk most nincs időm hogy részletesen leírjam.
Amikor az előzőt írtam, az az elején tényleg még megoldási ötlet volt csak és véletlenül úgy hagytam
|
|
|
| [692] Python | 2007-03-28 16:55:31 |
 Megoldási ötlet:
pl. R rajta van CD-n, mivel DRO +ORC +ORC =2.90o egyenesszög (Thalesz-tétel), és így mivel CD-re merőleges OR, CD-t R felezi, hasonlóan P, Q, S is ABCD oldalfelező pontjai. =2.90o egyenesszög (Thalesz-tétel), és így mivel CD-re merőleges OR, CD-t R felezi, hasonlóan P, Q, S is ABCD oldalfelező pontjai.
Ha felezési pontok, paralelogrammát alkotnak, hiszen PQ és RS AC-vel párhuzamos, QR és PS pedig BD-vel (háromszögközépvonalak).
Ha AOB = = , COD , COD =180o- =180o- (fél kerület, így fél középponti szög). (fél kerület, így fél középponti szög).  , és , és  . Ha ABCD átlóinak M a metszéspontja, MDA háromszögben . Ha ABCD átlóinak M a metszéspontja, MDA háromszögben  és és  , így AMD , így AMD =90o, tehát ABCD átlói merőlegesek. =90o, tehát ABCD átlói merőlegesek.
A feljebb említett párhuzamosságok miatt így PQRS valóban téglalap.
|
| Előzmény: [690] BohnerGéza, 2007-03-27 15:07:02 |
|
| [691] lorantfy | 2007-03-28 11:33:35 |
 109. feladat: Szerkesszünk négyzetet, ha adott mind a négy oldalegyenesének egy-egy pontja! (Nem volt még?)
|
|
|
| [689] Sirpi | 2007-03-26 09:46:35 |
 Amúgy ha már felmerült ez a feladat, akkor teljes indukcióval ugyanígy az is belátható, hogy a d dimenziós teret d-1 dimenziós alterekkel (azaz hipersíkokkal) legfeljebb ennyi részre lehet vágni:

|
| Előzmény: [683] Sirpi, 2007-03-24 21:51:16 |
|
| [688] BohnerGéza | 2007-03-25 22:12:54 |
 108. feladat: Az O kp-ú körön ebben a sorrendben felvett A, B, C és D pontokra igaz, hogy AB ív + CD ív a kör kerületének fele. Az OA, OB, OC és OD Thálesz-köre messe a "következőt" a P, Q, R illetve S pontban! Bizonyítandó, hogy PQRS téglalap!
|
|
|
| [686] epsilon | 2007-03-25 07:56:00 |
 Helló! Köszi mindannyiatoknak! A feladatot azért kezelem gyanakvóan, mert tudjuk, láttuk, hogy indukcióval olyasmit is lehet bizonyítani, ami nem igaz (pl 2 egymásutáni szám egyenlő, ha ezt igaznak feltételezzük, a következő lépés is kijön), tehát az bizonytalan, hogy a legfennebb n(n+1)/2 +1 felső korlát el is érhető, minden n-re? Üdv: epsilon
|
|
|
| [684] V Laci | 2007-03-24 21:52:41 |
 Szia.
Legfeljebb  részre osztja a síkot n db egyenes. Ezt teljes indukcióval láthatod be: az n. egyenes behúzása legfeljebb n+1 új síkrészt eredményezhet. részre osztja a síkot n db egyenes. Ezt teljes indukcióval láthatod be: az n. egyenes behúzása legfeljebb n+1 új síkrészt eredményezhet.
|
| Előzmény: [682] epsilon, 2007-03-24 21:33:09 |
|
| [683] Sirpi | 2007-03-24 21:51:16 |
 0 egyenes 1 részre, 1 egyenes 2 részre, majd a k. egyenes mind a korábbi k-1-et metszve k db. új részt hoz létre, így a válasz:
1+(1+2+...+n)=n(n+1)/2+1
|
| Előzmény: [682] epsilon, 2007-03-24 21:33:09 |
|
| [682] epsilon | 2007-03-24 21:33:09 |
 Heló! Tudna-e Valaki segíteni ebben a kérdésben: legtöbb hány részre osztja a síkor "n" darab egyenes? Előre is kösz! Üdv: epsilon
|
|
|
|
|
| [678] HoA | 2007-03-14 16:54:19 |
 Idézet következik Szénássy Barna korabeli magyar nyelven megírt írásából, melynek címe: Jelentés a császári és királyi inspektornak az helvét vallású kollégyum tiszta tudákosság leckéin végzett vizitációjáról.
"Hanem aztán az harmadik deák-klasszisban baj is lőn. Mikoron ugyanis junior Gyarmati praeceptor uram az lap-háromszögelléseket oktatván megkérdezé Toldallagi földmérő Ábris nevű fatytyát, mi jutna eszébe hallván eztet: kebel x, az deák válaszolá, neki bizon nyugalmazott enzsenőr kapitán Bolyai János szépséges Szöts Júlia nevezetű szolgáló-leána. Továbbiglan az praeceptor uram meg sem kérdezé az pótkebelt, az visszáskebelt és az visszás-pótkebelt." (Staar 1990: 129)
Nyilvánvaló, hogy egy matematikai fogalom megnevezésére a kebel szó nem a legalkalmasabb, hiszen ez a diákokban, elsősorban a fiúkban, más jellegű asszociációkat ébreszt. A kebel egyébként a hasonló jelentésű latin sinus magyarítására tett kísérlet volt.
Forrás: http://web.axelero.hu/pellestamas/Tamas/terminologia.htm
|
| Előzmény: [670] csocsi, 2007-03-13 16:42:54 |
|
|
| [676] Mumin | 2007-03-14 01:33:55 |
 AzO megoldása (én is segítettem):
Vegyünk két maximális távolságú pontot a sokszögben (A,B). Ha legalább az egyik belső pont (A), akkor növelni tudjuk a távolságot úgy, hogy a két ponton átmenő egyenes és a sokszög metszéspontjába visszük el A-t (természetesen B-től ellenkező irányba.) Tehát maximális távolságú pontpár csak a sokszög határán lehet.
Tegyük fel, hogy A egy oldal belső pontja. Ekkor B-től AB távolságra fekvő pontok egy körvonalon helyezkednek el, mely körvonalat az oldal érinti vagy metszi. Mindkét esetben növeljük tehát a távolságot, ha A-t mozgatjuk az oldal körvonalon kívül levő végpontjába (ilyen mindig van.) Tehát a sokszög határán elhelyezkedő pontpárok csak akkor lehetnek maximális távolságúak, ha csúcsokban vannak.
A csúcsban elhelyezkedő pontpárok közül pedig a legnagyobb távolságúnak a legnagyobb a távolsága.
|
| Előzmény: [657] HoA, 2007-02-26 16:03:28 |
|
|
| [674] BohnerGéza | 2007-03-13 20:25:33 |
 Bizonyítottnak vettem a 107. feladatot, melyet HoA [157]-ben javasolt. Így nem szükséges a gyök öt átmérőjű körökkel való lefedés. (Nem is lehet öt darabbal, esetleg ezt lehetne kitűzni feladatként.)
|
| Előzmény: [673] fermel, 2007-03-13 19:47:17 |
|
| [673] fermel | 2007-03-13 19:47:17 |
 Azt láttam, hogy öt tartomány van. A felosztás, ha nem is pontosan így, de nekem is megvolt. A problémám az, hogy mi a korrekt bizonyítása annak, hogy pld. egy "házikóban" a maximális távolság gyök öt. Tudom, hogy annyi,de ezt nekem nem sikerült tökéletesen bebizonyítanom. Gyök öt átmérőjű!! körrel kéne lefedni, de ilyet nem találtam. fermel
|
| Előzmény: [671] BohnerGéza, 2007-03-13 17:26:12 |
|
| [672] BohnerGéza | 2007-03-13 17:37:41 |
 Itt találtam: http://www.sg.hu/listazas.php3?id=1172238672
Tudtátok, hogy a nyelvújítás időszakában a sinust kebelnek akarták fordítani, a cosinus-t pótkebelnek, az arc-cosinus-t visszás-pótkebelnek. Aztán persze megbukott. Még az eredeti latin sinus szó is hibás fordítás eredménye, jelentése: öl, öböl, kebel. Az eredeti indiai szó húrt jelentet, ez arabul jiba, amiból jr-t írtak le. A középkori fordító jaib-ot értet ezalatt, ami öl vagy az öböl szája. Ebből lett a magyar kebel.
|
| Előzmény: [670] csocsi, 2007-03-13 16:42:54 |
|
| [671] BohnerGéza | 2007-03-13 17:26:12 |
 Talán megtévesztő az ábra, de csak öt szín van, tehát öt tartomány. Mivel a téglalap oldalát nem vesszük a tartományhoz, egy tartomány két pontja közt a távolság kisebb mint gyök öt.
|
| Előzmény: [669] fermel, 2007-03-13 13:10:45 |
|
| [670] csocsi | 2007-03-13 16:42:54 |
 Sziasztok! Nekem lenne egy trigonometriához kapcsolódó kérdésem. A kérdés a következő: hogy próbálták elnevezni a nyelvújítás során a szinuszfüggvényt? Ezt a kérdést órán kaptuk, és már égen földön kerestem, de még egy névhez sem tudtam kötni a kérdést sajnos. Remélem tudtok segíteni!
|
|
| [669] fermel | 2007-03-13 13:10:45 |
 Esetleg leírnád bővebben a gondolatmenetedet? Odáig rendben van, hogy az általad írtból következik az eredeti feladat megoldása,de sajnos nekem nem áll össze, hogy miért igaz, amit leírtál. Köszönöm fermel
|
| Előzmény: [662] BohnerGéza, 2007-03-05 18:01:50 |
|
| [668] Andras17 | 2007-03-09 15:48:35 |
 Kellene egy kis segítség. 2 lapot kaptam de van 4 geometriai feladat az egyiken (A geometria sajnos nem az erősségem). Itt van a feladatlap(az 1; 4; 5; 7 kellene):
http://img80.imageshack.us/img80/3689/matek0gd7.jpg
Bármilyen segítséget szivessen fogadok, mert van még egy hasonló lapom csak az meg egyenletekkel meg más feladatokkal van tele.
|
|
| [667] sakkmath | 2007-03-07 11:09:37 |
 A következő, nehéznek tűnő - még megoldatlan - feladatot én találtam ki. Minden idevágó észrevétel, ötlet, vélemény érdekelne akkor is, ha az nem párosul részleges, vagy teljes megoldással.
|
 |
|
|
|
| [664] Doom | 2007-03-05 20:23:21 |
 Mekkora a görbületi sugara egy R sugarú hengerpaláston egyenletesen ( szöggel) emelkedő csavarvonalnak? szöggel) emelkedő csavarvonalnak?
|
|
| [663] Cckek | 2007-03-05 18:25:58 |
 Helló. A következő érdekes problémákkal találkoztam a hétvégén:
1. Határozzuk meg az ABC háromszög azon belső pontját melynek a háromszög csúcsaitól mért távolságainak a szorzata maximális/minimális.
2. Határozzuk meg az ABC háromszög azon belső pontját melynek a háromszög oldalaitól mért távolságainak a szorzata maximális/minimális.
|
|
| [662] BohnerGéza | 2007-03-05 18:01:50 |
 Ha az ábrán az egy színnel jelölt tartomány egy pontja körül egy gyök öt sugarú kört rajzolunk, az az egész tartományt lefedi, így hat pont nem rakható le a téglalapon belül úgy, hogy bármely kettő távolsága legalább gyök öt legyen.
|
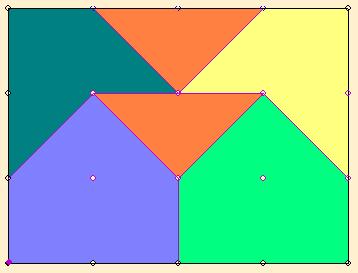 |
| Előzmény: [638] fermel, 2007-02-17 14:42:37 |
|
| [661] trizi | 2007-02-28 15:17:12 |
 epsilon! már meg is van az eredmény, köszi
|
|
| [660] epsilon | 2007-02-28 14:17:06 |
 Bizonyára tudod, hogy a körszelet területe T=r×r×(x-sinx)/2. Legyen O a kőr középpontja, AB a 210 cm hoszú húr, és legyen OM merőleges az AB húrra, M a talppont az AB húron. Legyen r a kör sugara, így pl. az OAB derékszögü háromszögben az átfogó r, a két befogó 105 illetve (r-50). Pitagorász tételével innen kijön az r. Továbbá az OAB háromszög területét 2 féle képpen felírjuk: 1/2×AB×OM=1/2×OB×OC×sinx vagyis 210×(r-50)=r×r×sinx és innen az r ismeretében megvan sinx és aztán x is.
|
|
| [659] trizi | 2007-02-28 12:36:49 |
 Sziasztok. Tud valaki segíteni körszelet területének kiszámításában, ha m=50 cm h=210 cm és más adatot nem ismerek?
|
|
| [658] jenei.attila | 2007-02-27 14:59:55 |
 A feltételből következik, hogy a szemközti oldalak hosszának összege egyenlő. Mivel konvex négyszögről van szó, ezért a négyszög érintő négyszög. Érintő négyszögben az egyik átló behúzásával keletkező két háromszög beírt körei érintik egymást. Ez csak vázlat, de nagyon könnyű bizonyítani ezeket az állításokat.
|
| Előzmény: [653] Csimby, 2007-02-23 01:20:45 |
|
| [657] HoA | 2007-02-26 16:03:28 |
 Javaslom 107. feladat nak [656] általánosítását: Bizonyítsuk be, hogy egy sokszöglapon két pont távolsága (a pontok a határon is lehetnek) nem lehet nagyobb, mint a sokszög két, egymástól legtávolabbi csúcsának távolsága.
|
| Előzmény: [656] fermel, 2007-02-25 13:01:40 |
|
| [656] fermel | 2007-02-25 13:01:40 |
 A 638-asban leírt feladattal kapcsolatban lenne még kérdésem. Azt kellene belátni, hogy egy 2x2-es házikóban(2x1-es téglalapon egy 2 alapú, 1 magasságú egyenlőszárú háromszög)két pont távolsága maximum négyzetgyök 5.(természetesen a pontok a határon is lehetnek) Köszönöm: fermel
|
| Előzmény: [638] fermel, 2007-02-17 14:42:37 |
|
|
|
| [653] Csimby | 2007-02-23 01:20:45 |
 106.feladat Egy konvex négyszög egyik átlóját behúzva, a kapott két háromszög beírható körei érintik egymást. Bizonyítsuk be, hogy a másik átlót behúzva ugyanez igaz. (Ma volt Arany Dani feladat 9.oszt.-osoknak)
|
|
| [652] BohnerGéza | 2007-02-23 00:42:22 |
 Köszönöm nadorp [642] tanulságos megoldását! Azt hiszem, ez és az alábbi alapján is kitalálhatunk új feladatokat.
A feladatra a B.3970 ([632]-ben is megtalálható) megoldásának keresése közben találtam, egy átmérő behúzása után a következőt észrevéve:
|
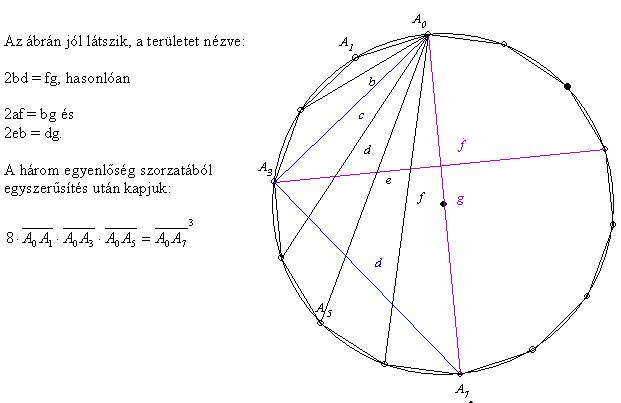 |
| Előzmény: [639] BohnerGéza, 2007-02-18 00:54:57 |
|
|
|
|
| [648] HoA | 2007-02-22 15:52:27 |
 Nagyon szép megoldás!
Azért leírom, szerintem mire gondoltak a feladat kitűzöi. Tekintsük a szabályos hétszög oldala és két különböző átlója által alkotott ABC  -et . -et .  , ,  =4. =4. , , =2. =2. , , = = . Vegyük észre, hogy mind az . Vegyük észre, hogy mind az  mind a mind a  szög felezője a szög felezője a  -et egy, az eredetihez hasonló és egy egyenlőszárú -et egy, az eredetihez hasonló és egy egyenlőszárú  -re bontja. Az elsőből -re bontja. Az elsőből  , a2=b2+bc , a másodikból , a2=b2+bc , a másodikból  , b2=c2+ac . Felhasználva, hogy c=1 , b2=c2+ac . Felhasználva, hogy c=1
(1) -ben a-t (2) -ből helyettesítve: (b+1)2.(b-1)2=b2+b=b.(b+1)
| a+b=(b+1)(b-1)+(b+1)(b-1)2=(b+1)(b-1)(1+b-1)=(b+1)(b-1)b | (5) |
végül
 | (6) |
|
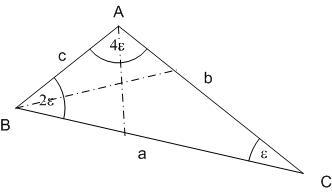 |
| Előzmény: [646] BohnerGéza, 2007-02-22 11:51:37 |
|
|
| [646] BohnerGéza | 2007-02-22 11:51:37 |
 A Ptolemaiosz-tétel szerint a négyszög átlói és oldalai közt igaz, hogy e*f <= a*c+b*d, ahol az egyenlőség húrnégyszögben és csak abban igaz.
Az ABCDEFG szabályos hétszög esetén alkalmazzuk a tételt pl. az ACDE négyszögre, ekkor e*f = a*e+a*f ahonnan az állítás következik.
|
| Előzmény: [636] BohnerGéza, 2007-02-12 22:00:07 |
|
| [645] lorantfy | 2007-02-22 08:38:32 |
 Szia Laura!
A három szögfelező kevés, kell még egy pont is.
Ha az adott pont mondjuk az A csúcs, akkor tükrözve a másik két szögfelezőre, mindkét pont a BC oldalra esik.Ezt meghúzva megvan B és C.
Ha egy D kerületi pont van megadva, akkor sorra tükrözzük a három szögfelezőre, addig, míg minden oldalon 2-2 pontot kapunk.
|
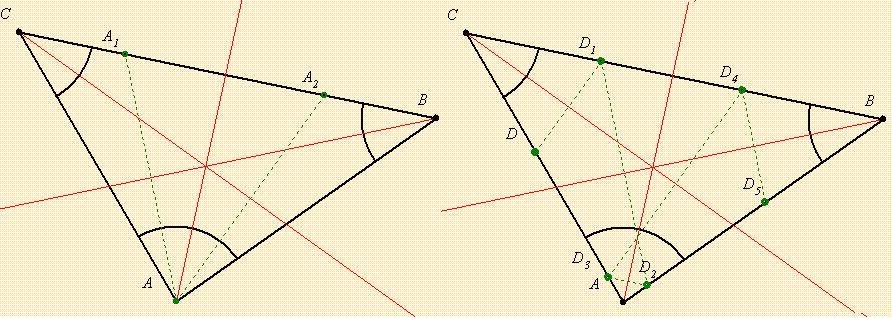 |
| Előzmény: [644] lauraa, 2007-02-21 19:07:11 |
|
| [644] lauraa | 2007-02-21 19:07:11 |
 sziasztok! nem tudja valaki, hogyan lehet megszerkeszteni egy 3szöget, ha adott 3 szögfelezője? köszi előre :-)
|
|
| [643] HoA | 2007-02-21 00:48:30 |
 Egy megoldás [619] mintájára: A szabályos hétszögnek 7 rövidebb és 7 hosszabb átlója van, ezek harmonikus közepe megegyezik egy rövidebb és egy hosszabb átló harmonikus közepével. Tekintsük az egységnyi oldalú ABCDEFG szabályos hétszög AC és AD átlóját. Azt kell igazolni, hogy  Legyen a hétszög körülírt köre k1, az inverzió k2 alapkörének középpontja A, sugara Legyen a hétszög körülírt köre k1, az inverzió k2 alapkörének középpontja A, sugara  . Mivel k1 átmegy A-n, inverze a BG egyenes, így C és D C' ill. D' képe is ide esik. Legyen AD és k2 metszéspontja H. . Mivel k1 átmegy A-n, inverze a BG egyenes, így C és D C' ill. D' képe is ide esik. Legyen AD és k2 metszéspontja H.   . Bizonyítandó: . Bizonyítandó:  , vagyis elég megmutatni, hogy , vagyis elég megmutatni, hogy  . Az ábrán zölddel jelölt ABG, BAC és CAD szögek . Az ábrán zölddel jelölt ABG, BAC és CAD szögek  nagyságúak, mert egy szabályos hétszög körülírt körében az oldalakhoz tartozó kerületi szögek. ABC' nagyságúak, mert egy szabályos hétszög körülírt körében az oldalakhoz tartozó kerületi szögek. ABC'  egyenlőszárú, egyenlőszárú,  = =  . AC a BAH középponti szög felezője, így BH felező merőlegese, . AC a BAH középponti szög felezője, így BH felező merőlegese,  . AC'H . AC'H  egyenlőszárú, AHC' szög = egyenlőszárú, AHC' szög =  . C'D'H . C'D'H  = AD'G = AD'G  = 3 = 3 mint az ABD' mint az ABD'  külső szöge. De ekkor a HC'D' külső szöge. De ekkor a HC'D'  -ben a HC'D' -ben a HC'D'  = = -4. -4. =3. =3. , HC'D' , HC'D'  egyenlőszárú, egyenlőszárú,  , amit igazolni akartunk. , amit igazolni akartunk.
|
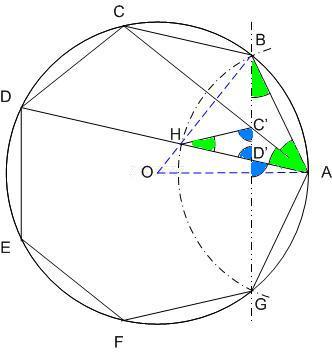 |
| Előzmény: [636] BohnerGéza, 2007-02-12 22:00:07 |
|
| [642] nadorp | 2007-02-19 08:51:18 |
 Ha a szabályos 14-szöget egységnyi sugarú körbe írjuk, akkor nyilván elég belátni, hogy A0A1.A0A3.A0A5=1. Legyen x az első 14-dik komplex egységgyök. ( nem akarok  -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt
A=A0A1.A0A3.A0A5=|x-1||x3-1||x5-1|=|(x-1)(x8-x3-x5+1)|=(x-1)(-x-x3-x5+1)|

|
| Előzmény: [639] BohnerGéza, 2007-02-18 00:54:57 |
|
|
|
|
| [638] fermel | 2007-02-17 14:42:37 |
 Egy kombinatorikai feladat megoldásában szeretném a segítségeteket kérni. Azért ide írom, mert a probléma végül is geometriai. Adott egy 3x4-es téglalap. Bizonyítsuk be, hogy bárhogyan is adunk meg benne 6 pontot, biztos, hogy található köztük kettő, melyek távolsága nem nagyobb , mint négyzetgyök 5! A feladat 7 pont esetén nagyon egyszerű. Felosztjuk a téglalapot 6 db 2x1-es téglalapra. Ez 6 skatulya. 7 pont közül biztosan van legalább kettő, amelyik ugyanabba a skatulyába tartozik, azon belül pedig a maximális távolság valóban négyzetgyök 5. Megfelelő skatulyák megválasztásával már 6 pontra is igaz. Sajnos nem találom az 5 részre való felosztás módját. Köszönöm a segítséget. (Elnézést a négyzetgyök 5 kezdetleges írásmódjától, de hiába írtam be Worldben jól, nem másolta át nekem ide.)
fermel
|
|
|
| [636] BohnerGéza | 2007-02-12 22:00:07 |
 Egy aktuális, de egyáltalán nem közismert feladat:
B. 3970. Bizonyítsuk be, hogy egy egységnyi oldalú szabályos hétszög átlói hosszának harmonikus közepe 2.
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [635] Doom | 2007-02-11 13:35:31 |
 Ilyenekre gondoltam, köszi mindkettőtöknek!
|
|
|
| [633] V Laci | 2007-02-11 12:06:34 |
 Én most hirtelen két geometriai példát tudnék mondani:
1) Trapézban, a átlók metszéspontján át húzott, az alapokkal párhuzamos egyenes trapézon belüli része a két alap harmonikus közepe.
2) Háromszög egyik szögfelezőjére, a szemközti oldallal való metszéspontjából állított merőleges kimetsz egy szakaszt az egyik oldalból. Ez a szakasz a szögfelezővel szomszédos két oldal harmonikus közepe.
Ilyen "geometriai jelentésre" gondoltál?
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [632] Doom | 2007-02-11 11:15:38 |
 Nem tudjátok véletlenül, hogy a harmonikus középnek milyen geometriai jelentése van? Előre is kösz!
|
|
|
|
|
| [628] BohnerGéza | 2007-02-06 20:48:35 |
 Nem tudom, hogy képességvizsga feladatnak a 8. osztályosok számára jó-e a feladat. Talán nem. (HoA hozzászólása is ezt erősíti bennem) A lényege általánosabban is használható.
Nem kell, hogy a BAD szög derékszög legyen. Jelöljük ezt a szöget fí-vel, ekkor 180 fok - fí forgatással oldhatjuk meg a feladatot. Ennek speciális esete, ha fí 0 fok ( az e egyenes egy partján van A és B, jussunk el A-ból e-t érintve B-be a legrövidebb úton ).
Gondolkodhatunk így is: Használjunk egy AA'-t tartalmazó síktükröt! Állítsuk úgy, hogy B'-ből lássuk benne D-t! ...
Nehezítek kicsit a feladaton: 104. feladat: Jussunk el minnél rövidebb úton B'-ből AA'-t és DD'-t érintve C-be úgy, hogy AA' és DD' között adott irányt kell követnünk! ( Az irányt az AA'D'D síkkal párhuzamos egyenessel adhatjuk meg. )
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [627] HoA | 2007-02-06 12:44:26 |
 Igen, a lényeg az, beugrik-e valakinek a síkba forgatás ötlete. Aki találkozott már a "pók legrövidebb útja a szoba falain a légyig" feladattípussal, annak persze nem nehéz.
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [626] Cckek | 2007-02-05 16:29:55 |
 Szép megoldás. Amúgy ez a feladat képességvizsga feladat a 8. osztályosok számára, itt Romániában, és ha nem ismertem volna hasonló módszert nem tudom hogyan lehetett volna 8. osztályos szinten megoldani.
|
| Előzmény: [625] BohnerGéza, 2007-02-05 12:34:31 |
|
|
| [624] Cckek | 2007-02-05 05:20:14 |
 103.feladat Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [623] Cckek | 2007-02-05 05:19:01 |
 102. Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [622] Csimby | 2007-02-02 10:37:26 |
 Köszönöm a sok szép megoldást :-)
|
|
|
|
|
| [618] Cckek | 2007-01-31 22:22:35 |
 Jelölje ia,ib,ic a háromszog szögfelezőit a,b,c az oldalait, írhatjuk:
 . .
Tehát csak annyit kell bizonyítani, hogy
 , ,
ami egyenértékű az
 , ,
egyenlőtlenséggel. De a

egyenlőtlenség miatt ez utóbbi fennáll.
|
| Előzmény: [617] Csimby, 2007-01-31 21:52:50 |
|
| [617] Csimby | 2007-01-31 21:52:50 |
 102.feladat Igaz-e és ha igen bizonyítsuk be, hogy tetszőleges háromszög szögfelezőinek a reciprokának az összege nagyobb az oldalai reciprokának az összegénél.
|
|
| [616] Cckek | 2007-01-31 21:43:36 |
 Nagyon érdekes feladat, főleg mivel általános iskolai színtű bizonyítást igényel. Egy ABCDA'B'C'D' téglatest éleinek a hossza a,b,c. Legyen Q AA'. Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen. AA'. Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen.
|
|
|
| [614] HoA | 2007-01-30 10:46:31 |
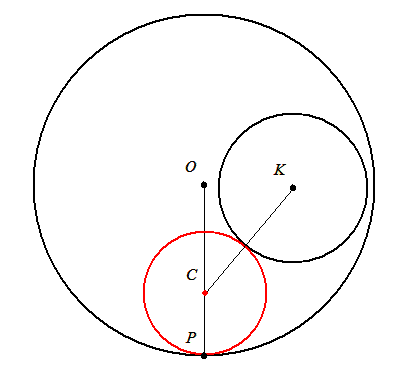
 A feladat a "Geometriai feladatok gyűjteményében" is szerepel. Az ottani megoldás sem bonyolult. Azon alapul, hogy a kis K2 kör és a szerkesztendő K3 kör T érintési pontja K2 és K3 hasonlósági pontja, és mivel C az OP egyenesen van, a hasonlóságban P megfelelője K2-n az OP-vel párhuzamos átmérő valamelyik végpontja (Q1, Q2). PQi kimetszi K2-ből T-t, TK és PO metszéspontja C. A választástól függően a K2-t kívülről illetve belülről érintő K3 kört kapjuk.
|
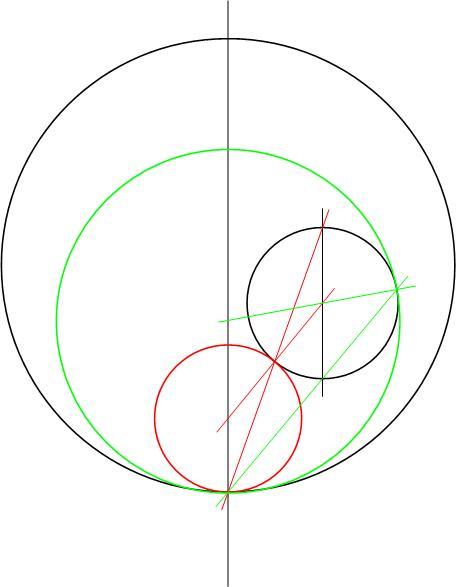 |
| Előzmény: [613] lorantfy, 2007-01-30 09:13:35 |
|
| [613] lorantfy | 2007-01-30 09:13:35 |
 Szia Attila!
Kösz a megolgást! Végülis ilyen egyszerű az egész. Szemléletesebb talán azt mondani, hogy az S pontban vegyünk fel egy r sugarú kört. Így két egyenlő sugarú körhöz kell érintőkört szerkesztenünk, tehát a keresett C pont rajta van a szimmetria tengelyen, vagyis KS felező merőlegesén.
|
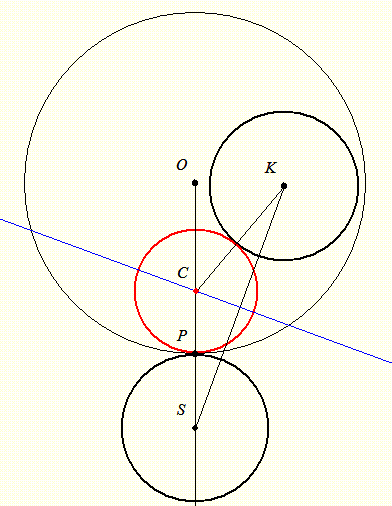 |
| Előzmény: [612] jenei.attila, 2007-01-29 14:01:30 |
|
|
| [611] lorantfy | 2007-01-27 11:14:46 |
 102. feladat: Adott az O középpontú R sugarú kör és belsejében az O-tól különböző, K középpontú r sugarú kör. Szerkesszönk olyan kört, mely a nagy kört egy adott P pontban érinti és érinti a kisebb kört is!
|
 |
|
| [610] BohnerGéza | 2007-01-25 12:11:02 |
 101. feladat: ( Megpróbálom, hátha sikerül sorszámozni a további feladatokat. )
|
 |
|
|
| [608] epsilon | 2007-01-11 11:49:45 |
 Köszi, megnéztem, hát onnan látszik a feladat "fajsúlya" ;-)
|
|
|
| [606] epsilon | 2007-01-11 11:14:12 |
 Hmmmm....hát kellett nekem :-) valóban implicit, mégis valamivel barátságosabbra gondolta, ez is a körszeletekből származik? Mert Én úgy próbáltam, hogy 2 szembennálló körszelet összegeként fogtam fel, a 2 körben, ott egzenlőre a sugár ami ismeretlen, meg 2 középponti szög, persze lehet kifejezni...de gyökös összefüggések lettek :-( Ha jó hallottam, ezt a feladatot valamikor a Danubiusz rádióban adták fel, és azt szeretném megtudni, hogy vajon milyen megoldást vártak volna el, pontosabban milyen eredményt, a helyes megoldásként...vagy csak szívatás volt?
|
|
|
|
| [603] epsilon | 2007-01-11 10:15:43 |
 Helló Cckek! Az igazolása affixumokkal csak algebrai számolás. Az illető csúcs megfelelő kisbetűjével jelölve az illető affixumot, a bizonyítandó összefüggés: 4(o1-h)+ 4(o2-h)+ 4(o3-h)= 15(g-h) vagyis 4(o1+o2+o3)=15g-3h és legyen a köréírt kör középpontja éppen az O origó, ekkor g=(a+b+c)/3 és h=a+b+c, és így elegendő bizonyítani, hogy: 2(o1+o2+o3)=a+b+c (*). Az előző indoklás alapján PO vektor=2 RO1 vektor (a az indoklást lásd előbb) és ezt affixumokkal felírva 0-p=2(o1-r)továbbá p=(b+c)/2, r=(m+n)/2 és az m, n a felezőpontokra vonatkozó affixumokat is használva, o1=a/2 adódik és analógjai (ezt még másképpen is bizonyíthatjuk) és a (*) összefüggés így valóban teljesül. (a bizonyítandó kép a hszm alján van!)
|
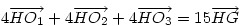 |
| Előzmény: [593] HoA, 2007-01-08 15:59:17 |
|
|
| [601] epsilon | 2007-01-10 22:07:38 |
 Kösz a megjegyzést, valóban ott van, most olvastam az ott leírt megjegyzéseket, ...de nem bíztatóak, valamilyen kifejezést szeretnék találni az R függvényében (nem megközelítő megoldást)de a körszeletekkel elindulva, két körszeletből összerakva egyenlőre semmi bíztató nem jött ki (még maradt kiküszöböletlen paraméter is :-(
|
|
| [600] psbalint | 2007-01-10 21:44:42 |
 azt hiszem éppen erről a feladatról volt szó az Érdekes matekfeladatok topikban
|
|
| [599] epsilon | 2007-01-10 20:48:52 |
 Helló! BÚÉK Mindenkinek! Létezik-e elemi megoldás a következő, ismertnek tűnő feladatra: Adott egy 1 egységsugarú körlap. Annak kerületén vegyünk fel egy tetszőleges M pontot, és az M középponttal, R sugárral rajzoljunk egy körívet, ami az adott körlapot két kükönböző pontban metszi. Mekkora kell legyen az R, hogy a "közrezárt" síkrész területe az 1 sugarú kör területének a fele legyen? Előre is kösz az esetleges támpontokat! Üdv: epsilon
|
|
| [598] HoA | 2007-01-10 15:51:57 |
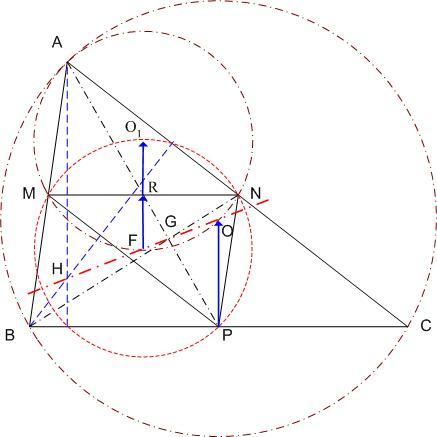
 A bizonyítás, ahol egy 3-as szorzóval elszámoltam magamat :-) : Cckek jelöléseivel ( ha már... ), legyen a körülírt kör középpontja O, a Feuerbach köré F, MN felezőpontja R. ABC  az AMN az AMN  A-ból vett kétszeres nagyítása, így A-ból vett kétszeres nagyítása, így  . AMN . AMN  és PNM és PNM  egymás tükörképei R-re, ezért egymás tükörképei R-re, ezért  , vagyis , vagyis  . .
 Hasonlóan Hasonlóan  és és  A hármat összeadva A hármat összeadva  és és  kiesik, mert egy kiesik, mert egy  súlyvonalainak harmadai, így vektorösszegük súlyvonalainak harmadai, így vektorösszegük  . Igazolandó : . Igazolandó :  . Legyen az Euler-egyenesen . Legyen az Euler-egyenesen  . Ekkor . Ekkor  , ,  és és  . Egyenlőségünk tehát . Egyenlőségünk tehát  , amit már nem nehéz belátni. , amit már nem nehéz belátni.
|
 |
| Előzmény: [595] HoA, 2007-01-09 11:13:46 |
|
|
|
|
| [594] Cckek | 2007-01-08 21:12:11 |
 Legyen G az ABC háromszög súlypontja, H az ortocentruma, M, N, P az AB, AC, BC oldalak felezőpontjai, O1,O2,O3 az AMN, BMP illetve CNP háromszögek köré írt körök középpontjai. Bizonyítsuk be hogy : 
|
|
| [593] HoA | 2007-01-08 15:59:17 |
 Mivel két hete senki sem szólt hozzá, leírok egy megoldást. Nézzük meg, mi a mértani helye a síkban azoknak a pontoknak, melyekre az ABC  csúcsaitól mért távolságok négyzetösszege csúcsaitól mért távolságok négyzetösszege
adott konstans?

 Ha origónak az ABC Ha origónak az ABC  S súlypontját választjuk, S súlypontját választjuk,  ; ;  , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha  (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor  . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De  Origó választásunk miatt Origó választásunk miatt  Innen Innen  Tehát valóban Tehát valóban 
|
| Előzmény: [588] BohnerGéza, 2006-12-25 22:50:17 |
|
| [592] Sirpi | 2007-01-05 16:10:42 |
 Ezt hívják Euler-egyenesnek, és ráadásul az S pont harmadolja (O-hoz közelebb) az OM szakaszt.
Egybe akkor és csak akkor esnek, ha a háromszög szabályos.
|
| Előzmény: [591] Cckek, 2007-01-05 16:04:29 |
|
| [591] Cckek | 2007-01-05 16:04:29 |
 Igaz-e, hogy bármely háromszögben az ortocentrum, a súlypont és a háromszög köré írt kör középpontja kollineárisak? (vagy egybeesnek:)
|
|
|
| [589] HoA | 2006-12-27 10:11:54 |
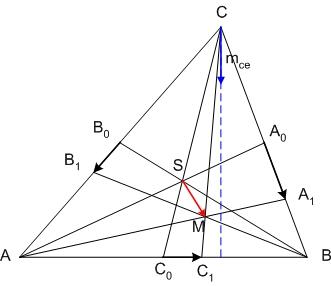
 BohnerGéza ábrája alapján ha az  , , , , paraméterekkel kifejezett koordinátákra felírjuk az paraméterekkel kifejezett koordinátákra felírjuk az  vektoregyenletet, rövid számolás után kapjuk, hogy vektoregyenletet, rövid számolás után kapjuk, hogy  = = = = , vagyis P (Cckek-nél M) = , vagyis P (Cckek-nél M) =  , vagyis M a súlypont. , vagyis M a súlypont.
Ha [582] "akkor" ágának bizonyítására elfogadjuk az [586] ábráját, a "csak akkor" ágra itt egy - talán kicsit szemléletesebb - bizonyítás. Legyenek a háromszög oldalfelező pontjai A0,B0,C0 , a súlypont S, továbbá M, A1,B1,C1 [582] szerint. A súlyvonalak a háromszöget hat kis háromszögre osztják. Az általánosság megszorítása nélkül feltehetjük, hogy M a C0BS háromszög belsejében vagy határán van. Mivel pl.  és tudjuk, hogy és tudjuk, hogy  , ,  pontosan akkor teljesül, ha pontosan akkor teljesül, ha
 | (1) |
. Ha a három vektor összege 0, akkor tetszőleges irányú vetületüké is az. Tekintsük az mc magasságra vett vetületeket - az mce egységvektorral vett skaláris szorzatokat. Ez  esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így  és és  . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S. . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S.
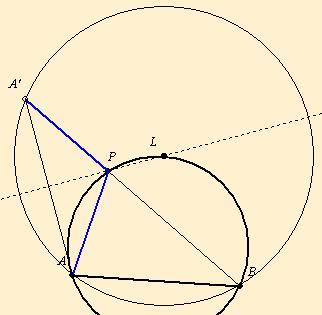
|
 |
| Előzmény: [587] BohnerGéza, 2006-12-25 22:49:35 |
|
|
|
|
| [585] HoA | 2006-12-23 09:19:45 |
 Azt hiszem az ellentmondás feloldása az, hogy Ti szakaszokról beszéltek, a feladat pedig vektorokról szól: az AA1, BB1, CC1 vektorok pontosan akkor alkotnak vektorháromszöget , ha M a súlypont. Lehet, hogy Cckek ezt akarta a szögletes zárójelekkel jelezni.
|
| Előzmény: [584] Cckek, 2006-12-22 21:02:28 |
|
|
| [583] jenei.attila | 2006-12-22 20:21:22 |
 Ezt sajnos nem értem. Azt akarod mondani, hogy ha a súlyponttól csak egy "kicsit különböző" pontot veszünk, akkor a szóbanforgó szakaszokból nem szerkeszthető háromszög? Ezek a szakaszok az M pont megválasztásával nyilván folytonosan változnak, tehát a súlyponttól való kis eltérés a hosszukban is kis változást eredményez. A háromszög egyenlőtlenségbe pedig még biztos hogy belefér egy kis változás. Valamit nyilván félreértek, pontosítanád egy kicsit?
|
| Előzmény: [582] Cckek, 2006-12-22 16:56:49 |
|
| [582] Cckek | 2006-12-22 16:56:49 |
 Legyen M az ABC háromszög egy belső pontja. AM,BM,CM a szemközti oldalakat metsze rendre az A1,B1,C1 pontokban. Bizonyítsuk be, hogy [AA1],[BB1],[CC1] szakaszok akkor és csak akkor egy háromszög oldalai ha M az ABC háromszög súlypontja.
|
|
| [581] Hajba Károly | 2006-11-23 15:30:14 |
 Én sem.
Az [577]-es válaszom után még motoszkált valami a fejemben és elkezdtem firkálgatni (a pitagórászi ábrácskára a köröket, az ábra jobb felső sarkában) és belémcsapot az isteni szikra. :o)
|
| Előzmény: [580] AzO, 2006-11-23 15:06:26 |
|
|
|
| [578] Hajba Károly | 2006-11-22 08:47:12 |
 Csimby!
Nem számoltál még be, hogy mire jutottatok?
---
Én közben találtam egy "igaz" 6 körös megoldást, ebben nincs mérés miatti körzőmozgatás:
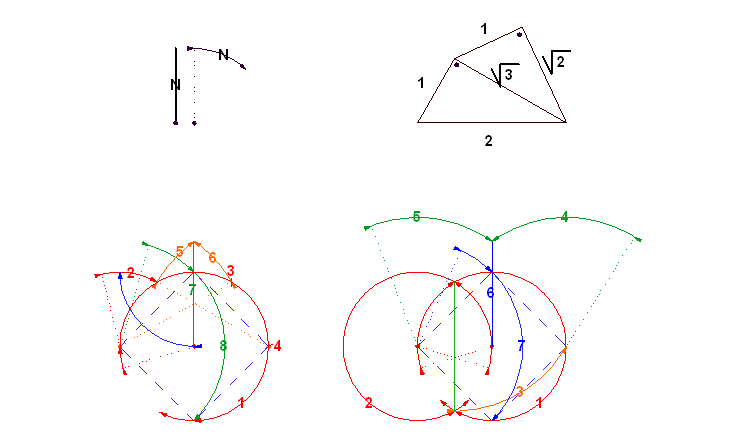
|
 |
|
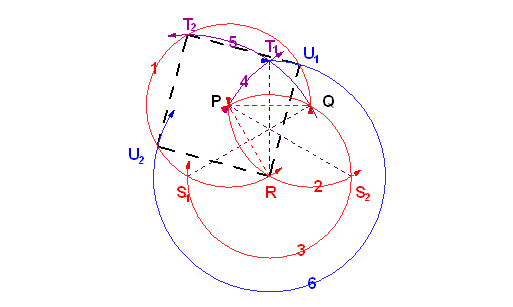
| [577] Hajba Károly | 2006-11-22 00:07:35 |
 Én fenn a Gellért-hegyen egy csillagász szakkörön hallottam és főleg a középiskolásoknak adták föl, én ott csak vízhordó voltam. :o)
Szóval a szakkörvezető így kezdte: Már az ókori görögök is ...
A definició, najó legyen csak "definició" szerint ScarMan megoldása valóban 7 körző-felemeléses, mert a 3. lépés távolságát használja fel a 4. és 5. lépésben. Lásd az ábrámat, melyen az én megoldásomat és az övét is felszerkesztettem.
Értelmező ábrácska a bal felső fekete, vastag vonal: mérés, nyilazott ív: körzőzés.
ScarMan-nak meg még egy grat.
|
 |
| Előzmény: [576] AzO, 2006-11-21 23:10:25 |
|
| [576] AzO | 2006-11-21 23:10:25 |
 Az 1977-es feladatot nem Napoleon-feladat-nak hivjak? Mintha olvastam volna valahol mostanaban. A definiciomert nem vallalok felelosseget, mert csak emlekezetbol mondtam, es akkor az en 7 lepeses megoldasom is mar 8 :)))
|
| Előzmény: [575] Hajba Károly, 2006-11-21 08:33:01 |
|
| [575] Hajba Károly | 2006-11-21 08:33:01 |
 Üdv a körösöknek! és grat ScarMan-ek is!
Nem kekeckedni szeretnék, de AzO definiciója szerint - körző felvétele a lépés vége - csak 8 lépésből lehet megszerkeszteni. Az alább közöltem megoldás 7 körzőzés és 1 mérés, ScarMan-nek 6 körzőzés és 2 mérés. S gyanítom, hogy a feladatban nem véletlen volt 8 lépés kitűzve, főleg ELTE matekon.
Mellesleg alább -habár gyanítom nem eléggé értelmezhető módon- az én megoldásom is ott van. Volt ez pár éve kérdés az "Éredekes matekfeladatok"-ban, akkor megoldottuk, ha jól emlékszem, Jenei Attila adta a másik megoldást. (4.1, ill. 4.2)
Az akkori megoldásomban a két adott pont a négyzet két sarokpontja, ehhez +1 körzőzés kell, de így szerintem más sem tudja rövidebben, míg az eddig megismert egyéb megoldásnál az egyik pont nem a négyzet sarokpontja, hanem a közepe. Ezt szerkesztette meg korábban J. A.
Én anno 1977-ben így hallottam a feladatot: Osszunk négy egyenlő részre egy körívet csak körző használatával! (Akkor 8-ikos koromban a feladat győzött. :o) Ez -a fenti definíció szerint- 7 lépésből megoldható, mivel adott volt már egy körív.
|
| Előzmény: [574] AzO, 2006-11-20 22:59:09 |
|
| [574] AzO | 2006-11-20 22:59:09 |
 Szerintem is 6 lepes. Grat! :)
|
|
|
| [572] ScarMan | 2006-11-20 20:18:42 |
 Itt egy 7-lépéses megoldás: két adott pont: A, B, mindkét pontból AB sugarú köröket rajzolunk, ezek metszéspontja: C, D. C-ből D-n átmenő kört rajzolunk -> B'. B és B' középpontú, CD sugarú köröket rajzolunk. Egyik metszéspontjuk E. B-ből EA sugarú kört rajzolunk (itt külön lépésnek vettem, hogy körzőnyílásba vesszük EA-t), ez kimetsz két pontot az eredeti A középpontú körből. Ez a két pont B-vel és B'-vel négyzetet alkot.
|
 |
|
| [571] psbalint | 2006-11-20 17:45:50 |
 Tévedek akkor ha azt mondom hogy ezt a feladatot az egyik Gerőcs-féle Repeta matek kötetben is meg lehet találni?
|
|
| [570] Mumin | 2006-11-20 16:18:51 |
 Szabad a gazda. Az évfolyamból több embernek elég volt 7 körzőhasználat is, és ez a megoldás nem is túl bonyolult. A lényeg: a Pithagorasz-tétel.
|
| Előzmény: [560] AzO, 2006-11-14 22:54:59 |
|
| [569] The Student | 2006-11-18 12:26:13 |
 Ha megígéritek, hogy én is ilyen okos leszek, akkor lehet, hogy elmegyek matematikusnak! :) Na jó üdv mindenkinek! Én
|
|
| [568] Hajba Károly | 2006-11-17 20:17:57 |
 OK köszi, sejtem a dolgot. :o)
Ha bevetem a Pappos-tételét, akkor már egy tetszőleges P ponta tudok egy e egyenessel párhuzamost fektetni -egy körzővel-. De hogyan kell merőlegest? Ill. visszatérve a négyzetre: adott két pont, mely a négyzet két sarokpontja. Hogyan tudom a kétféle négyzetet megszerkeszteni?
|
| Előzmény: [566] jonas, 2006-11-17 17:56:10 |
|
|
| [566] jonas | 2006-11-17 17:56:10 |
 Rendben, mutatom hogy szerkesztek négyzetet egy körzővel. Valószínűleg ennél sokkal egyszerűbb módszer is van, de ez jutott eszembe elsőként.
Először is elmondom, hogy lehet csak vonalzóval két adott párhuzamos egyeneshez egy harmadik párhuzamos egyenest szerkeszteni adott ponton át. Ez a Desargues-tételen alapul. Legyen e és f a két párhuzamos egyenes, és G1 az adott pont. Vegyünk fel egy tetszőleges O pontot. Legyen az OG1 egyenes metszéspontja e-vel illetve f-fel E1 illetve F1. Egy másik, az O-n átmenő tetszőleges egyenes az e és f egyenest az E2 és F2 pontban metszi. Legyen E1F2 és E2F1 metszete P. A G1F2 és az OP metszete legyen Q. Ez után az F1Q és az OF2E2 egyenesek metszete legyen G2. Végül G1G2 lesz a keresett g párhuzamos egyenes. (Én matematikus vagyok, ezért ezt a szerkesztést csak elméletben tudom elvégezni, valódi vonalzóval nagyon pontatlan lesz, de mivel te mérnök vagy, talán el tudod helyezni úgy a pontokat, hogy ne legyen túl nagy eltérés.)
Ha már ezt tudjuk, akkor a négyzet sem okozhat nehézséget. Ugyanis legyen k egy K középpontú kör. Ha most AB a kör egy húrja, akkor összekötve őket K-val az átmérők másik végpontjai C és D, így kapunk egy ABCD téglalapot. Ezután a téglalap párhuzamos oldalegyenesihez szerkeszthetünk K-n át párhuzamost, így kapunk két merőleges átmérőt, amiknek a végpontjai egy négyzetet határoznak meg.
|
| Előzmény: [565] Hajba Károly, 2006-11-17 08:51:12 |
|
|
| [564] josie | 2006-11-16 13:31:42 |
 szabályos testekről és a gúláról kénne minden!!!
|
|
|
| [562] S.Ákos | 2006-11-15 18:47:30 |
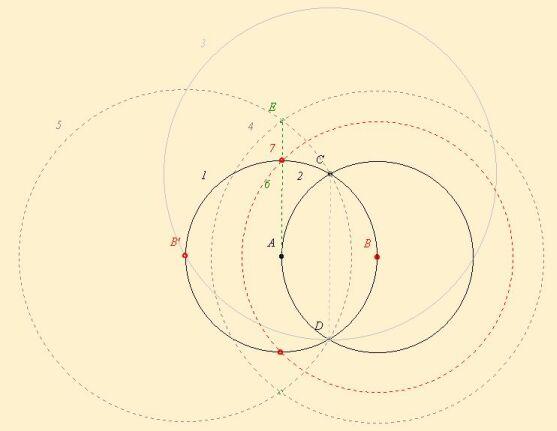
 Egy kissé egyszerűbb kérdés: mennyi a minimális körzőhasználatok száma, ha vonalzót is használhatunk?
|
|
|
| [560] AzO | 2006-11-14 22:54:59 |
 Tenyleg ne aruld el hetfoig!!! Csak korzo hasznalata engedelyezett. Egy lepes addig tart, amig fel nem emeled a korzot. 2 pont adott a sikon, es kell 4 metszespont, ami negyzetet alkot. Legfeljebb 8 lepeses megoldas eseten +1 jegy a vizsgan.
|
| Előzmény: [556] Hajba Károly, 2006-11-14 20:55:26 |
|
|
|
|
| [556] Hajba Károly | 2006-11-14 20:55:26 |
 Nem mondok több infót, csak kérdezek. :o)
A feladat szerint egy üres papírra kell köríveket rajzolni úgy, hogy 4 darab metszéspont épp egy négyzetet adjon ki? és ehhez legfeljebb 8 körív rajzolható? A köríven egy tetszőleges pont bejelőlése az lépés?
Vagy adott két pont és erre kell négyzetet szerkeszteni?
|
| Előzmény: [552] Csimby, 2006-11-14 18:38:13 |
|
|
|
| [553] The Student | 2006-11-14 18:45:19 |
 Így lesz, remélem! Itt szerintem amúgy sem a feladatról van szó, hanem a 8 lépésről nem? Nekem csak az a lényeg, hogy a feladat menjen! És azt sem tudod még megszerkeszteni? Vagy csak a 8 lépéses dolog nem megy neked?
|
|
| [552] Csimby | 2006-11-14 18:38:13 |
 Pont azt kértem, hogy több infót itt NE közöljetek mert az egész évfolyam körzővel mászkál az egyetemen annyira lázba hozott mindenkit a téma és nem lenne jó ha itt lelőné valaki a poént amit egyenlőre még én sem tudok :-) Szóval Studenttel beszéljétek meg e-mailben...
|
| Előzmény: [549] Hajba Károly, 2006-11-14 08:30:05 |
|
| [551] The Student | 2006-11-14 16:43:44 |
 A megoldásodhoz fűznél egy kis magyarázatot, mert azért 10.es létemre nem annyira értem :)
|
|
| [550] The Student | 2006-11-14 16:24:19 |
 Köszi, aki segített, majd kibogarászom! És a Batthyány Kázmér gimibe :D csak nekünk ilyen jófej példákat kellene megoldani 10.-ben :D Hát nem vicces, de kapok érte ötöst... Üdv: Én
|
|
|
| [548] Csimby | 2006-11-14 01:43:26 |
 Ja és légyszi több infót ne közöljetek erről a példáról ugyanis ma adták fel az ELTE matematikus szakán és aki jövő hétig 8 lépésből megoldja +1 jegyet kap a geometria vizsgán.
|
| Előzmény: [547] Csimby, 2006-11-14 01:28:57 |
|
|
|
|
| [544] BohnerGéza | 2006-11-13 22:15:45 |
 Az [533]-ban lévő feladatra:
Az [537]-ben jenei.attila írt vázlatosan erről: A nem kisebbik ív nyilvánvaló. A két oldal összeadásához tükrözzük A-t az APB= gamma szög külső szögfelezőjére: A'. Ekkor BA' a keresett összeg. BA'A= gamma/2. A' az AB gamma/2 látókörén van, ennek középpontja L. BA' a leghosszabb, ha átmérője a látókörnek, azaz P=L.
|
 |
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
| [543] The Student | 2006-11-13 20:48:32 |
 Srácok fogy az idő (és lányok) valamit nem segítenétek, emrt én ehhez nem vagyok elég... Előre is köszi!
|
|
| [542] fermel | 2006-11-13 20:38:09 |
 Csimby és Attila! Nagyon köszönöm a segítségeteket.
Attila! Azt,hogy B' is rajta van azon a bizonyos körön, hogyan láttad be? Én szögekkel próbálkoztam, de még nem jött ki. Lehet, hogy túlbonyolítom? Segítenél? Köszönöm.
fermel
|
|
| [541] The Student | 2006-11-13 20:29:40 |
 Látom, ez is egy használható tanács volt! Köszi
|
|
|
|
| [538] The Student | 2006-11-13 18:49:08 |
 Sziasztok, új vagyok itt, de remélem sikerül érdekes témákat hoznom, illetve segítenem, bár eléggé tudtalan vagyok! Tudna nekem valaki segíteni, hogy hogy lehet megszerkeszteni csak körzővel egy négyzetet? Ha igen, akkor kérlek gyorsan írjatok, mert kell a házimba :) Köszi!
|
|
| [537] jenei.attila | 2006-11-13 11:12:11 |
 Ha jól emlékszek, ez nem rég kömal feladat volt. Vegyük a PA PB közül a hosszabbikat (pl. PA-t), ezt P felé meghosszabítva B'-t vegyük fel úgy, hogy PB'=PB legyen. Ekkor PA+PB=AB'. F legyen a z hosszabbik AB ív felezőpontja. Könnyű bizonyítani, hogy az F középpontú körön, amely átmegy A-n és B-n, rajta van B' is. Ezért a kérdéses összeg akkor maximális, ha AB' átmérője az F középpontú körnek.
|
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
