| [119] S.Ákos | 2024-10-06 16:07:34 |
 20. kerdes a 37. feladat alapján -
a mutassuk meg, hogy tetszoleges \(\displaystyle \varepsilon>0\)-ra es minden eleg nagy \(\displaystyle n\)-re letezik tablazat, amiben a legnagyobb elem legfeljebb \(\displaystyle (1+\varepsilon) n^2 \ln n\) (ez persze explicit egyenlotlensegge teheto valamifele \(\displaystyle n^2 \ln n+f(n)\) formaban ahol \(\displaystyle f(n)=o(n^2\ln n)\)). Van-e erosebb felso becslesunk?
|
|
| [118] BerkoErzsebet | 2024-10-06 08:52:59 |
 Héttusa 39. feladata. A nyomozó 6 nap alatt biztosan megtalálja a bűnöst. Az ilyen típusú feladatoknál szoktam olyanra is gondolni, attól függetlenül, hogy kiolvasható-e a szövegből vagy nem, az, hogy kell-e ilyenre gondolnunk, hogy mondjuk 5 nap adataiból egy nálam sokkal többet látó valaki, már tudja a bűnöst. Mindketten ugyanazt nézzük, de van, aki nálam sokkal többet lát. /Talán kicsi a valószínűsége./
Nagyon tanulságos a 31. feladat (labdarúgó-bajnokság). Milyen könnyen lehet elsőből utolsó!
|
|
| [117] Szemerédi Ferenc | 2024-10-04 11:29:56 |
 Ha jól számolom a 19. kérdés következik és nekem ez pont a 19. feladat általánosított átfogalmazása: A kör kerületén felvett n db pont legfeljebb hány hegyesszögű háromszöget határoz meg?
|
|
|
| [115] Káli gúla | 2024-10-03 17:24:18 |
 Addig akkor megvan, hogy a régi győztes mérlege pozitív (több győzelem, mint vereség), az új győztesé negatív.
Legyen a két csapatnak \(\displaystyle \omega, \omega'\) győzelme és \(\displaystyle \delta, \delta'\) döntetlene. Ha a vessző nélküli számok tartoznak az új bajnokhoz, akkor a helycsere feltétele:
\(\displaystyle 2(\omega-\omega')+\delta-\delta' < 0 < 3(\omega-\omega')+\delta-\delta' ,\)
amiből átrendezéssel azonnal adódik, hogy \(\displaystyle \omega>\omega'\), sőt a
\(\displaystyle 2(\omega-\omega')<\delta'-\delta< 3(\omega-\omega')\)
szigorú egyenlőtlenség miatt \(\displaystyle \omega-\omega'\ge2\) és így \(\displaystyle \delta'-\delta\ge5\), méghozzá \(\displaystyle \omega-\omega'=2\) esetén \(\displaystyle \delta'-\delta=5\).
Ha \(\displaystyle \omega=3\), akkor \(\displaystyle \omega'\ge1\) miatt csak \(\displaystyle \omega'=1\) lehet, így a régi győztes mérkőzéseinek száma pontosan \(\displaystyle 1+(\delta+5)+0\), az új győztesé viszont legalább \(\displaystyle 3+\delta+4\) lenne, ami lehetetlen. Tehát a régi győztesnek legalább 4 győzelme volt.
|
| Előzmény: [113] Szemerédi Ferenc, 2024-10-03 08:29:04 |
|
| [114] BerkoErzsebet | 2024-10-03 10:11:00 |
 A feladatban az volt, hogy legalább 7 csapat indul. Meg lehet valósítani 10 csapattal. A 1 gy, 8 d, 0 v B-I 1 gy, 7 d, 1 v J 4 gy, 0 d, 5 v Én csak azt használtam, amit a feladatban leírtak. Más dolgok felhasználása csak kiegészítheti az alapfeladatot, szerintem. Különböző országokban különbözőféleképpen döntik el pontegyenlőség esetén, hogy a bajnokságokon ki a győztes.
|
| Előzmény: [113] Szemerédi Ferenc, 2024-10-03 08:29:04 |
|
| [113] Szemerédi Ferenc | 2024-10-03 08:29:04 |
 31. feladat alternatív megoldása, csak azért nem tetszik nekem, mert gólarányokról a feladatban nem volt szó, bár lehet hogy ez mindenkinek egyértelmű (nekem nem, de igaz én eddig azt se tudtam hogy 3 pontot kap a győztes, nem követem a sportot) Én az alábbi megoldást adtam:
Lehetséges (Régi pontozás szerint minden meccsen két pontot osztanak ki ezért az átlagos végső pontszám csapatonként = résztvevőkszáma-1. A vesztesnek ennél kevesebbet kell kapnia (és ekkor értelemszerűen lesz legalább egy csapat aki ennél többet kapott) Így a győztesnek legalább két ponttal volt több. Ha régi pontozásról áttérünk újra akkor mindenki a meglevő pontszámához kap még annyi pontot ahány győzelme volt. Hogy a "régi vesztes" új győztes legyen akkor legalább 3 ponttal kell többet kapnia (mert 2 pont különbség biztos volt köztük) mint a régi győztes (és a győztesnek kell lennie legalább egy nyert meccsnek), tehát ha a régi vesztesnek 4 győzelme és 5 veresége volt, a nyertesnek 1 győzelme és 8 döntetlen, mindenki másnak 1 győzelem, 7 döntetlen és 1 vereség akkor az megfelelő. Ez előállhat úgy hogy A (ő a régi nyertes) megveri B-t mindenki mással döntetlent játszik. A többi meccsek 4 db hármas körbeverése (x legyőzi y-t, y legyőzi z-t,z legyőzi x-t) úgyhogy B szerepel mindegyik hármasban. Minden más meccs döntetlen. A fentiekből következik, hogy ha a régi vesztesnek legalább 4 győzelemmel kell rendelkeznie (és így van az átlag alatt), akkor az átlag pontszám régen legalább 9, a résztvevők száma legalább 10.
|
| Előzmény: [110] Keresztvölgyi József, 2024-09-13 17:59:44 |
|
|
|
| [110] Keresztvölgyi József | 2024-09-13 17:59:44 |
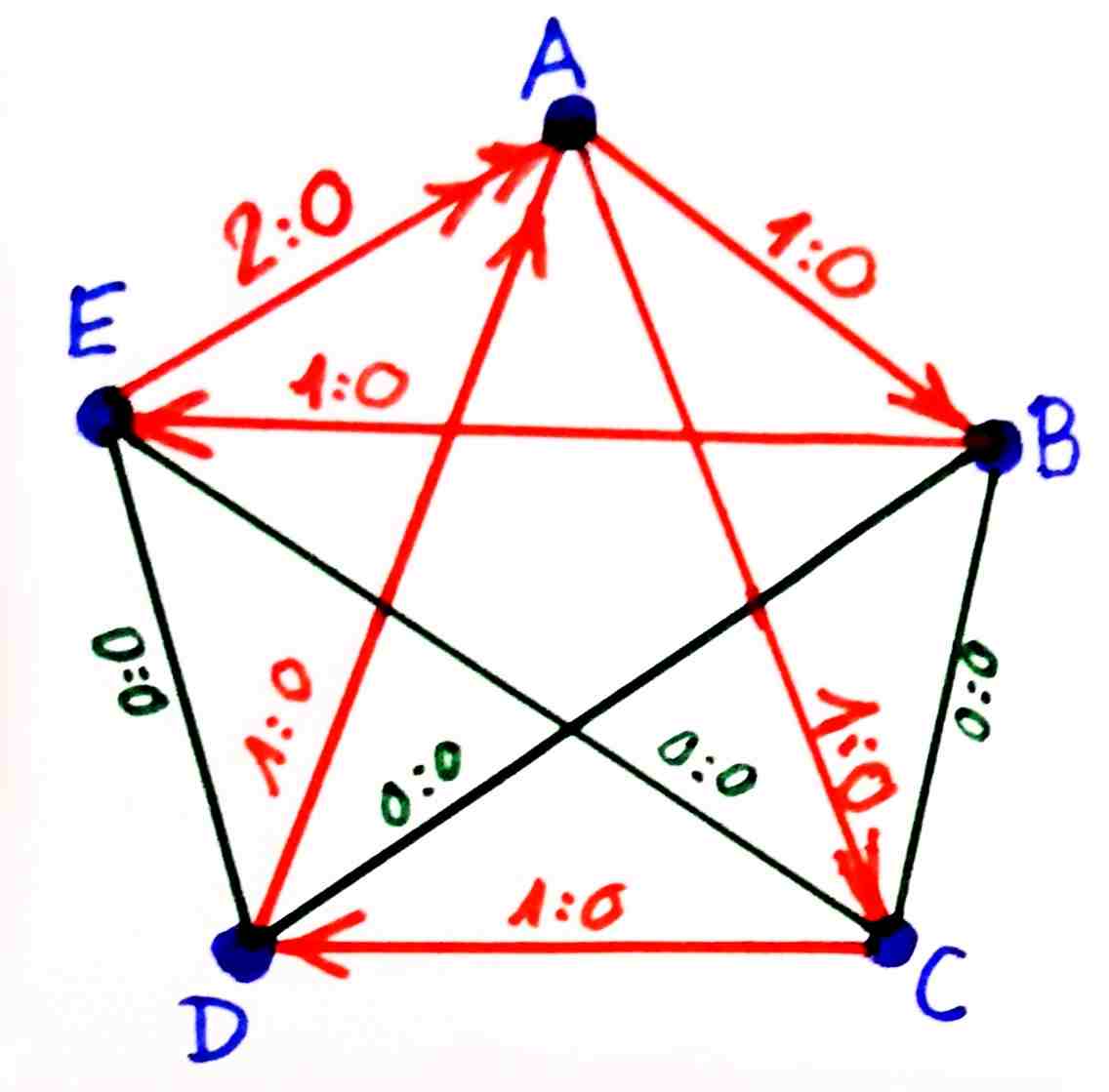
 A Héttusa 31. feladatának egy alternatív megoldása:
31. Egy labdarúgó-bajnokságon legalább 7 csapat indul, és bármely két csapat pontosan egy mérkőzést játszik egymással. Lehetséges-e, hogy a bajnokság győztese a régi pontozási rendszer szerint az utolsó helyen végezne?
A mostani pontozás szerint a mérkőzés győztese 3 pontot, a vesztes 0 pontot kap, döntetlen esetén pedig 1-1 pontot kap a két csapat. A régi rendszer abban különbözik a jelenlegitől, hogy a győzelemért 3 pont helyett 2 pont jár.
Ez lehetséges minden olyan bajnokságban, ahol az induló csapatok száma legalább 5.
Például 5 csapat indulása és a lehető legkevesebb gól esetén (ha további 6., 7., 8. . . csapat indul, és azoknak az összes mérkőzésük döntetlen, akkor is az A csapat az utolsó vagy az első, a régi vagy a mostani pontozás szerint):
|
 |
|
| [109] Sheriwoyama | 2024-09-12 12:28:55 |
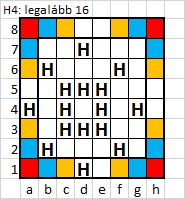
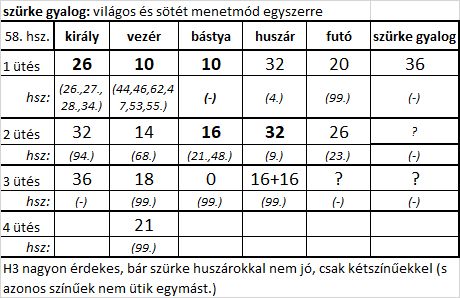
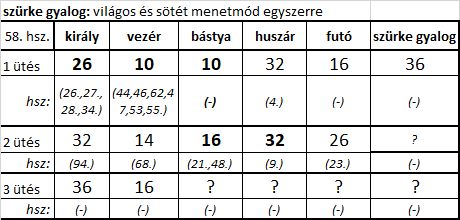
 A 100-adik hozzászólás táblázatában a Huszárok 4 ütéssel rovatba egy "16 ?" bejegyzést eszközölhetünk a mellékelt ábra alapján. A színezések indoklása a K4-éhez hasonló. A tökéletes szimmetriához a 7×7-es sakktábla volna az igazi.
|
 |
|
| [108] Róka Sándor | 2024-09-10 15:25:39 |
 Megjelent a Héttusa új fordulója \(\displaystyle \to\) 6. forduló
A beküldési határidő október 1.
Ezt követően itt is beszélgethetünk a feladatokról.
|
 |
|
| [107] Sheriwoyama | 2024-09-08 15:26:38 |
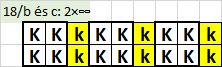
 A 18. kérdéshez:
A 2×végtelen esetre példa az alábbi ábra. A sárgított királypárokban mindig csak 1-et meghagyva máris végtelen sok a lehetőség. Az így kapott 2-soros sávot szintén lehet fölfelé másolni, miáltal a fölső félsík vagy pl. a 8×végtelen sáv kitöltését is megkaphatjuk. (1 üres sort legalább hagyni kell a másolatok között.)
Máris van tehát végtelen sok példánk, az "összes" alapváltozatot talán Harold Scott MacDonald Coxeter tudta volna meghatározni...
|
 |
|
| [106] Sheriwoyama | 2024-09-08 15:13:25 |
 A 18. kérdéshez:
A teljes síkot megcélozva a, z egyszínű mezőket fel is lehet fújni 2×2-es négyzetekké (változat 1), de ki is ritkíthatjuk (változat 2). Van egy 3. változat is, kétféle szemlélettel. Ez egy srégen vonuló minta, amelyet eltologatva újabb kitöltéseket kapunk. Bár e kitöltés szó talán nem pontos, hiszen véges sok sáv esetén elég ritkás a mintázat.
|
 |
|
| [105] Sheriwoyama | 2024-09-08 15:04:13 |
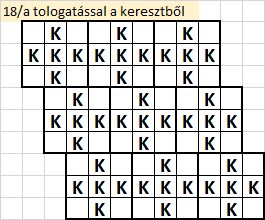
 A 18. kérdéshez:
A keresztnek elnevezett király-csoportokat 3 soronként lehet jobbra vagy balra eltologatni - ami máris végtelen sok variációt jelent. Példa:
|
 |
|
| [104] Káli gúla | 2024-09-07 14:31:02 |
 "A végtelen sakktábla viszont kitölthető például ..."
Mivel a minden irányban végtelen sakktáblán a csak sötét (csak világos) mezőkre rakott a királyok ugyanígy négy másikat ütnének, felmerül a következő
18. kérdés. Hány különböző elrendezés van a) a végtelen táblán, b) a felső félsíkon, c) egy \(\displaystyle 8\times\infty\) sávban, amelyben mindegyik király pontosan négy másikat támad?
|
| Előzmény: [103] Sheriwoyama, 2024-09-07 12:50:07 |
|
| [103] Sheriwoyama | 2024-09-07 12:50:07 |
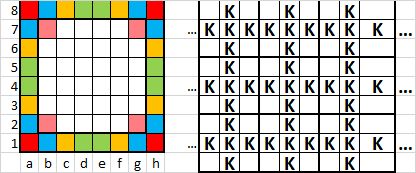
 Királyok 4 ütéssel nem helyezhetők a sakktáblára!
A sarkokba nem kerülhet király, hiszen csak 3 szomszédjuk van. b1-en álló királynak éppen 4 szomszédja marad, ezért a2-re is kerül király. Annak egyértelműen a3 és b3 szomszédjait kell elfoglalni újabb királyokkal. Csakhogy akkor b2K-t 6 kolléga fogná közre. Vagyis b1 és a2, meg elforgatottjaik szabadok! c1K-nak így pont 4 szomszédja van, ekkor c2K lefogja b3,c3,d3-at, ezáltal b2K-nak már nem lehet 4 király-ütője. Vagyis c1 kizárva, a tükörképeivel együtt. b2-nek ezért csak 3 szomszédja marad, vagyis nem lehet rajta király. d1-nek éppen 4 király-szomszédja volna, ekkor a d2K c3,d3,e3 kizárásával c2K-nak már nem lehet 4 szomszédja. Vagyis d1, e1 és tükörképeik is szabadok kell, legyenek. Ekkor tehát ott tartunk, hogy a tábla szélén nem lehet király. Vagyis a maradék 6×6-os táblára kellene tenni a királyokat. De ott sem lehet a sarkokba tenni - vagyis az elejétől ismételhetjük a gondolatmenetet. Így jutva a 4×4-es, majd 2×2-es tábláig, ahol már minden mező sarokmező. A végtelen sakktábla viszont kitölthető például az alábbi 5-királyos "kereszt"-ekkel:
|
 |
|
|
| [101] Sheriwoyama | 2024-08-30 15:20:47 |
 Sajnos nem tudok 2 képet egyszerre bevinni, így külön következnek az ábrák - és gúlától elnézést a dupla ékezetért :-)
|
 |
|
| [100] Sheriwoyama | 2024-08-30 15:18:09 |
 Káli gűla mindent ismer, így csak azért foglalom össze, hogy jól lássék egy helyen az aktuális tudásunk...
|
 |
|
| [99] Káli gúla | 2024-08-29 10:52:11 |
 32 huszár, mindegyik pontosan 3 másikat üthet: https://puzzling.stackexchange.com/questions/94766/knights-attacking-exactly-three-knights
18 vezér, mindegyik 3 másikat üthet: https://kvant.mccme.ru/pages.html 2009/4 borító (Némi utánolvasással kiderül, hogy királynőkre ez egy régi puzzle, több helyen is felbukkant, Scott Kim zseniális dizájnertől származik. Érdemes elolvasni a róla szóló teljes fejezetet Martin Gardner The Last Recreations c. könyvében.)
Bástyából nem lehet pontosan 3 ütéses sereg: a bal alsó sarokhoz legközelebbi max kettőt (fel és jobbra állót) tud támadni.
20 futó, mindegyik 1 másikat üthet: https://puzzling.stackexchange.com/questions/94421/chess-pieces-attacking-exactly-once/94479#94479
Huszárok, mindegyik pontosan 1 másikat üthet: 32-nél többet nem lehet, a táblát lefedjük négyes ciklusokkal, valamelyik négyelemű ciklusba 2-nél több bábu kerülne. https://www.linux-magazine.com 2018/211/knight-s-tour/figure-2
Huszárok, mindegyik pontosan 2 másikat üthet: 32-nél többet nem lehet. Programmal végignéztem, és nem talált 32-nél nagyobb halmazt.
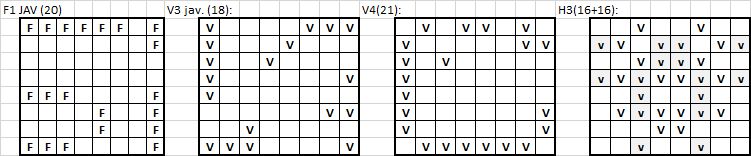
17. kérdés. (a) Helyezzünk el a sakktáblán 30 huszárt úgy, hogy mindegyik pontosan 2 másikat támad. (b) Helyezzünk el a sakktáblán 38 huszárt úgy, hogy mindegyik legfeljebb 2 másikat támad. (c) Hány huszárt lehet elhelyezni a sakktáblán úgy, hogy mindegyik pontosan 4 másikat támad?
|
| Előzmény: [97] Sheriwoyama, 2024-08-28 22:08:13 |
|
|
| [97] Sheriwoyama | 2024-08-28 22:08:13 |
 Néhány új elrendezés (amiket eddig nem találtam).
|
 |
|
| [96] Sheriwoyama | 2024-08-28 21:57:13 |
 Kiegészíteném Róka Sándor táblázatát.
Elnézést, ha valamin átsiklottam...
|
 |
|
| [95] Káli gúla | 2024-08-25 23:41:23 |
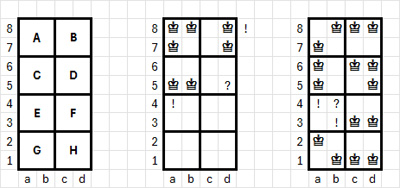
 8. kérdés. Királyok pontosan 2 ütéssel kérdésre a válasz 32. Több nem lehet, ez valamennyire pepecselős, de megoldható kézzel. Tegyük fel, hogy 33 király van a táblán, és mindegyik 2 másikkal szomszédos. Ekkor például a bal oldali féltáblán 16-nál, és pl. a bal felső negyedben 8-nál több bábu van. Felosztjuk a táblát 2x2-es kis négyzetekre az ábra szerint. Egy háromkirályos négyzet bábui ciklust alkotnak, az ilyen királyokkal szomszédos mezők mindig üresek. Emiatt 2 háromelemű négyzet nem lehet egymás mellett, ha pedig csúcsban találkoznának (pl. \(\displaystyle A,D\)), akkor a másik két négyzet (\(\displaystyle B,C\)) legfeljebb egyelemű lehetne. Tehát a bal felső negyedben csak 9=3+2+2+2 kiosztásban lehetnek bábuk. Sem \(\displaystyle |B|=3\), sem \(\displaystyle |C|=3\) nem lehet, mert abból \(\displaystyle |A|=1\) következne az a8 különleges helyzete miatt. Tehát vagy \(\displaystyle |A|=3\), vagy \(\displaystyle |D|=3\).
A középső ábra mutatja az \(\displaystyle |A|=3\) esetet. \(\displaystyle B\) csak a második oszlopában tartalmazhatja a két királyt, ekkor a d8 a másik szomszédos királlyal (e7 vagy e8) hármas ciklust alkot, így blokkolja a c6, d6 mezőket. Hasonlóan blokkolt a c5, c6 mezőpár is \(\displaystyle C\) oldaláról, tehát \(\displaystyle D\)-ben legfeljebb csak d5-ön lehetne bábu, ami viszont ellentmondás.
A jobb oldali ábrán látszik a \(\displaystyle |D|=3\) eset. Belátjuk, hogy \(\displaystyle |E|+|F|+|G|+|H|\le7\). Feltehetjük, hogy \(\displaystyle E,F,G,H\) egyike sem 3 elemű, mert \(\displaystyle E\) a \(\displaystyle C\)-beli, \(\displaystyle F\) a \(\displaystyle D\)-beli elrendezés miatt biztosan nem az, \(\displaystyle |H|=3\) esetén \(\displaystyle |F|\le1\) és \(\displaystyle |G|\le1\), tehát \(\displaystyle |E|+|F|+|G|+|H|\le7\) adódna, ha pedig \(\displaystyle |G|=3\) lenne, abból \(\displaystyle |E|=1\) és \(\displaystyle |H|=1\) vagy \(\displaystyle |F|=1\) következne, azaz ismét \(\displaystyle |E|+|F|+|G|+|H|\le7\) adódna. Ha tehát \(\displaystyle F,G,H\) kételeműek, akkor – ilyen sorrendben nézve – csak az ábra szerinti párokat tartalmazhatják. Így viszont b4-re nem kerülhet bábu, mert a2 árván maradna, tehát a5 csak a4-en, c3 csak b3-on folytatható, ami b3-nál hibához vezet. Ez ismét ellentmondás, ami tehát igazolja, hogy 32-nél több király nem lehet ezzel a tulajdonsággal.
A 32 király elérhető, de csak két körrel, a külső kör a sarkok nélkül 24 peremmezőből áll, a belső kör ugyanígy 8 mező a középső 4x4-es négyzet szélén. Összefüggő, húr nélküli királykör legfeljebb 31 elemű lehet, ezt megkapjuk, ha a 24 peremmezőből álló kört jobbról "benyomjuk" a h7-g6-f6-e6-d6-c5-c4-d3-e3-f3-g4-h3-h2 görbe mentén.
Ha viszont pontosan 2 helyett legfeljebb 2 ütést kívánnánk, akkor már lehet 33 király a táblán: az egyik sarok 3 szomszédján, és további három, ezzel párhuzamos, de sarok nélküli L-alakú csoportban.
|
 |
| Előzmény: [94] sakkmath, 2024-08-25 21:31:45 |
|
